Rumus Persamaan Garis Lurus Beserta Contoh Soal – Dalam pelajaran Matematika terdapat materi pembelajaran tentang persamaan garis lurus. Apa itu persamaan garis lurus? Persamaan garis lurus sering disebut sebagai persamaan linier yang merupakan persamaan yang terdiri dari satu variabel atau lebih. Persamaan garis lurus selalu berkaitan dengan gradien. Tanpa adanya gradien maka persamaannya tidak dapat diketahui, kecuali berpotongan antara kedua titik. Bagaimana cara menyelesaikan soal soal persamaan garis lurus itu?
Saat terjun menyelami materi, kita tidak hanya belajar pengertiannya saja tpai ada pula rumus persamaan garis lurus yang wajib dihafalkan. Dengan demikian barulah kita bisa mengerjakan contoh soal secara akurat. Dalam persamaan tersebut pada umumnya mengandung beberapa variabel di dalamnya dengan rumus yang berbeda beda.
Di lain sisi, perbedaan tingkat kesulitan pada contoh soal persamaan garis lurus pun juga sering disuguhkan oleh guru. Tujuannya tak lain sebagai bentuk pendalaman materi mengingat banyak siswa yang kesulitan pada saat mengerjakannya. Pada kesempatan kali ini saya akan menjelaskan tentang rumus persamaan garis lurus beserta contoh soal persamaan garis lurus.
Rumus Persamaan Garis Lurus Beserta Contoh Soal
Persamaan garis lurus ialah perbandingan koordinat x dengan koordinat y yang terletak di antara dua titik pada garis. Dalam rumus dan contoh soal persamaan garis lurus terdapat gradien didalamnya. Apa itu gradien? Gradien ialah perbandingan antara komponen x dengan komponen y yang akan membentuk kecondongan garis. Gradien dilambangkan dengan huruf “m”.
Gradien tersebut merupakan salah satu penunjang rumus persamaan garis lurus yang tersedia. Sebelum membahas tentang materi persamaan garis lurus tersebut, anda harus mengetahui berbagai rumus untuk menghitung gradien tersebut.
Baca juga : Rumus dan Sifat Logaritma Beserta Contoh Soal Logaritma
Gradien Persamaan Garis Lurus
Bukan suatu rahasia lagi apabila mengetahui siswa kesulitan menghafal rumus hitung. Padahal rumus tersebut jadi modal awal untuk mengerjakan soal secara tepat. Nah, untuk menyelesaikan persamaan garis lurus maka kalian harus mengetahui konsep gradien terlebih dulu.
Persamaan ax + by + c = 0
Untuk persamaan ax + by + c = 0 tersebut memiliki gradien yang dapat dicari dengan rumus dibawah ini:

Melalui Titik (a,b) dan Titik Pusat (0,0)
Selanjutnya terdapat rumus gradien yang melalui titik (a,b) dan titik pusat (0,0) yaitu:

Melalui titik (x1,y1) dan titik (x2,y2)
Selanjutnya adapula rumus yang digunakan untuk mencari gradien melalui titik (x1,y1) dan titik (x2,y2) yaitu:

Garis yang Dilalui Sejajar
Untuk garis yang dilaluinya sejajar secara umum memiliki gradien yang dapat dicari dengan rumus seperti dibawah ini:

Garis yang Dilalui Tegak Lurus
Untuk garis yang dilaluinya tegak lurus dapat menggunakan prinsip lawan dan kebalikan. Adapun rumus gradiennya yaitu:

Rumus rumus pada gradien diatas berkaitan dengan materi persamaan garis lurus tersebut. Untuk menyelesaikan contoh soal persamaan garis lurus ini, maka sebelumnya anda harus mencari besar gradiennya terlebih dahulu. Setelah itu baru menentukan persamaan garis lurus menggunakan rumus yang ada.
Rumus Persamaan Garis Lurus
Rumus pada persamaan garis lurus dapat dibagi menjadi beberapa macam. Seperti rumus pada persamaan garis lurus yang melalui titik pusat (0,0) dan bergradien m, melalui titik (0,c) dan bergradien m, melalui titik (x1,y1) dan bergradien m, serta melalui titik (x1,y1) dan titik (x2,y2). Berikut penjelasan selengkapnya:
Baca juga : Rumus Statistika Dasar Matematika Beserta Contoh Soal
Melalui Titik Pusat (0,0) dan Bergradien m
Persamaan garis lurus yang melalui titik pusat (0,0) dan bergradien m yaitu:
y = mx
Melalui Titik (0,c) dan Bergradien m
Titik (0,c) merupakan titik potong pada sumbu y. Berikut rumus persamaan garis lurus yang melalui titik (0,c) dan bergradien m yaitu:
y = mx + c
Melalui Titik (x1,y1) dan Bergradien m
Berikut rumus pada persamaan garis lurus yang melalui titik (x1,y1) dan bergradien m yaitu:
y – y1 = m (x – x1)
Melalui Titik (x1,y1) dan Titik (x2,y2)
Persamaan garis lurus yang melalui titik (x1,y1) dan titik (x2,y2) ini dapat dicari menggunakan rumus yaitu:

Contoh Soal Persamaan Garis Lurus
Dibawah ini terdapat beberapa contoh soal persamaan garis lurus beserta pembahasannya:
1. Hitunglah persamaan garis lurus yang memiliki gradien -2/3 dan melalui titik pusat koordinat!
Pembahasan
Diketahui : m = -2/3 dan titik pusat (0,0)
Ditanyakan : Persamaan Garis Lurus = ?
Jawab :
y = mx
y = -2/3 x
3y = -2x
2x + 3y = 0
Jadi, persamaan garis lurusnya ialah 2x + 3y = 0.
2. Tentukan persamaan garis lurus yang gradiennya 4/6 dan melalui titik (0,-3)!
Baca juga : Metode Penyelesaian Sistem Persamaan Linier Dua Variabel (SPLDV) Lengkap
Pembahasan
Diketahui : m = 4/6 dan titik (0,-3)
Ditanyakan : Persamaan Garis Lurus = ?
Jawab :
Contoh soal persamaan garis lurus ini dapat dicari menggunakan rumus tertentu. Adapun rumus persamaan garis lurus yang digunakan yaitu:
y – y1 = m (x – x1)
y – (-3) = 4/6 (x – 0)
y + 3 = 4/6 x
6(y + 3) = 4x
6y + 18 = 4x
-4x + 6y + 18 = 0
Jadi, persamaan garis lurusnya ialah -4x + 6y + 18 = 0.
3. Tentukan persamaan garis lurus yang dilalui oleh titik (2,3) dan titik (-3,5)?
Pembahasan
Diketahui : titik (2,3) dan titik (-3,5)
Ditanyakan : Persamaan Garis Lurus = ?
Jawab:
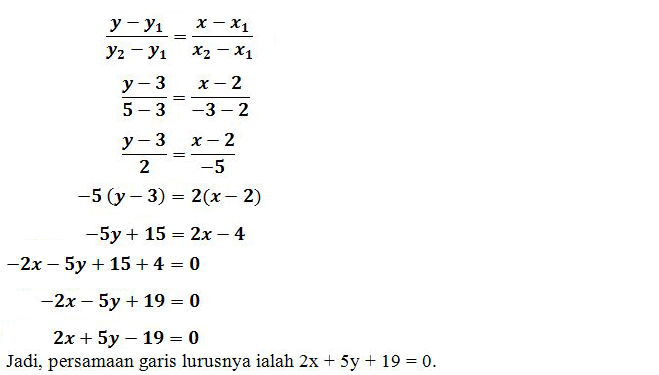
Sekian penjelasan mengenai rumus persamaan garis lurus dan contoh soal persamaan garis lurus. Dalam menentukan persamaan garus lurus, sebelumnya anda harus menghitung nilai gradiennya terlebih dahulu. Setelah itu baru menentukan persamaannya menggunakan rumus yang ada. Penggunaan rumus ini harus disesuaikan dengan garis yang melaluinya. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.


