Cara Menyelesaikan Persamaan Linear Satu Variabel dan Contoh Soal – Persamaan linear dalam Matematika tidak hanya berupa dua variabel saja, tetapi juga berbentuk satu variabel. Cara menghitung persamaan linear satu variabel hampir sama dengan dua variabel. Tetapi dalam contoh soal persamaan linear satu variabel tersebut pengerjaannya lebih mudah dan simple dibandingkan dua variabel. Persamaan Linear Satu Variabel (PLSV) ialah pernyataan simbol Matematika yang memiliki satu variabel dengan pangkat 1 dan dipisahkan oleh tanda sama dengan (=). Sistem persamaan ini menyatakan dua hal yang sifatnya sama.
Sesuai dengan namanya bahwa PLSV memiliki variabel yang jumlahnya hanya satu. Meskipun hanya satu, namun beberapa siswa masih menganggap materi yang satu ini sulit untuk dikerjakan. Sebenarnya anda tidak perlu khawatir jika dihadapkan dengan soal soal PLSV tersebut. Hal ini dikarenakan persamaan linear satu variabel memiliki rumusnya sendiri dalam pengerjaan soal soalnya. Dengan begitu pengerjaan soal PLSV akan lebih mudah untuk dilakukan.
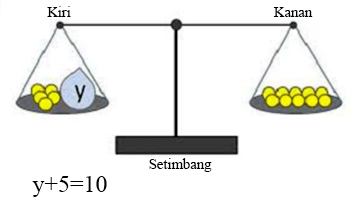 |
| Rumus menghitung persamaan linear satu variabel |
Gambar di atas merupakan ilustrasi mengenai persamaan linear satu variabel. Ketika dibangku sekolah, para siswa diajarkan mengenai persamaan linear dua variabel dan satu variabel ini beserta cara menyelesaikannya. Bahkan persamaan ini sering digunakan dalam soal soal ujian. Nah pada kesempatan kali ini saya akan menjelaskan tentang cara menyelesaikan persamaan linear satu variabel beserta contoh soal persamaan linear satu variabel. Untuk lebih jelasnya dapat anda simak di bawah ini.
Cara Menyelesaikan Persamaan Linear Satu Variabel dan Contoh Soal
Sebelum membahas tentang cara menghitung dan contoh soal persamaan linear satu variabel tersebut. Saya akan membagikan bentuk umum dari PLSV terlebih dahulu. Persamaan linear satu variabel memiliki bentuk umum yaitu:
ax + b = c atau
ax = b dimana a ≠ 0
Keterangan :
x = Variabel (lambang variabel tersebut dapat diganti dengan sembarang huruf)
a, b, dan c = Konstanta (melambangkan bilangan tertentu)
Baca juga : Metode Penyelesaian Sistem Persamaan Linear Dua Variabel (SPLDV) Lengkap
Dalam penyelesaian PLSV, anda harus mengetahui beberapa kalimat yang terkandung didalamnya. Hal ini dikarenakan kalimat tersebut berpengaruh terhadap cara menyelesaikan persamaan linear satu variabelnya. Contohnya persamaan kalimat terbuka x + 7 = 13. Jika nilai x nya diganti dengan bilangan cacah berangka 4 maka akan menjadi kalimat salah. Tetapi jika x diganti dengan angka 6 maka akan menjadi kalimat benar. Perhatikan contoh berikut ini!
x + 7 = 13 (Kalimat Terbuka)
4 + 7 = 13 (Kalimat Salah)
6 + 7 = 13 (Kalimat Benar)
Catatan :
- Persamaan linear ini mempunyai satu variabel yakni x.
- Variabel ini mempunyai pangkat 1 dan biasanya tidak ditulis. Seperti penulisan x sama dengan x¹.
- Angka yang terletak didepan variabel dinamakan Konstanta.
- Angka yang tidak disertai variabel dinamakan Konstanta. Contoh 3x + 4 = 10, maka konstantanya adalah 4 dan 10.
- Jika dalam satu persamaan terdapat dua penulisan variabel yang sama, maka akan tetap dianggap hanya mempunyai satu variavel saja. Contohnya 2x + 3 = 3x + 3.
Cara Menyelesaikan Persamaan Linear Satu Variabel
Cara menghitung persamaan linear satu variabel dapat dibagi menjadi beberapa macam yaitu substitusi, melalui persamaan ekuivalen, mengurangi atau menambah bilangan yang sama pada kedua ruas, serta membagi atau mengalikan bilangan yang sama bukan angka nol pada kedua ruasnya. Berikut penjelasan selengkapnya beserta contoh soal persamaan linear satu variabelnya:
Substitusi
Cara pertama dalam menyelesaikan persamaan linear satu variabel ialah dengan subtitusi. Cara ini harus memperhatikan beberapa hal penting seperti :
- Mengetahui teknik perkalian, pembagian, penjumlahan dan pengurangan (x, :, +, -).
- Mengetahui ketentuan ketika persamaan berpindah dari ruas kanan ke kiri dan sebaliknya. Jika sebelumnya bernilai positif (+) maka akan berubah menjadi negatif (-) apabila berpindah ruas, begitu pula sebaliknya. Kemudian jika sebelumnya merupakan perkalian maka akan berubah menjadi pembagian apabila berpindah ruas, begitu pula sebaliknya.
Baca juga : Rumus Persamaan Garis Lurus Beserta Contoh Soal
Hal hal diatas perlu anda perhatikan ketika menggunakan cara substitusi dalam PLSV. Berikut contoh soal persamaan linear satu variabelnya:
Contoh Soal
1. 2x = 12 Berapakah nilai x?
Jawab.
2x = 12
x = 12/2
x = 6
Jadi nilai x = 6.
2. 2x + 28 = 0, hitunglah nilai x?
Jawab.
2x + 28 = 0
2x = -28 (bernilai negatif karena berpindah ruas)
x = -28/2
x = -14
Jadi nilai x = -14.
Melalui Persamaan Ekuivalen
Cara menyelesaikan persamaan linear satu variabel selanjutnya ialah melalui persamaan ekuivalen. Persamaan ekuivalen ialah persamaan yang kedua nilai himpunannya sama dan sebanding. Berikut contoh soalnya:
2x = 12
2x : 2 = 12 : 2
x = 6
Mengurangi atau Menambah Kedua Ruasnya
Cara menghitung persamaan linear satu variabel selanjutnya ialah dengan mengurangi atau menambah kedua ruasnya. Kedua ruas PLSV dikurangi atau ditambah dengan angka yang sama hingga memperoleh hasil akhirnya. Berikut contoh soalnya:
2x + 6 = 4x – 10
Pembahasan.
2x + 6 = 4x – 10 (sederhanakan dengan menghilangkan angka 6 dengan -6 pada kedua ruas)
2x + 6 – 6 = 4x – 10 – 6
2x = 4x – 16 (sederhanakan dengan menghilangkan 2x dengan -2x pada kedua ruasnya)
2x – 2x = 4x – 16 – 2x
0 = 2x – 16
-2x = -16 (kedua ruasnya dibagi dengan -2)
-2x : -2 = -16 : -2
x = 8
Membagi atau Mengalikan Kedua Ruasnya
Cara menyelesaikan persamaan linear satu variabel selanjutnya ialah dengan membagi atau mengalikan kedua ruasnya. Kedua ruas PLSV dibagi atau dikali dengan angka yang sama hingga memperoleh hasil akhirnya. Berikut contoh soalnya:
Baca juga : Rumus dan Sifat Logaritma Beserta Contoh Soal Logaritma
2x = 18
Pembahasan.
2x = 18 (sederhanakan kedua ruasnya dengan membagi 2)
2x : 2 = 18 : 2
x = 9
Contoh Soal Persamaan Linear Satu Variabel
Selain contoh soal diatas, adapula contoh soal persamaan linear satu variabel lainnya. Contoh soal ini diambil dari penerapan aktivitas sehari hari. Berikut contoh dan pembahasannya:
1. Rina membeli 4 buku tulis dengan harga Rp 10.000. Berapakah harga satu buku tulisnya?
Jawab.
Buku tulis diibaratkan dengan variabel x
4x = 10.000
x = 10.000/4
x = 2.500
Jadi harga satu buku tulisnya adalah Rp 2.500.
2. Rani membeli 4 penghapus dengan uang Rp 5.000, tetapi ia masih mendapatkan kembalian Rp 1.000. Berapakah harga satu buah penghapusnya?
Jawab.
Penghapus diibaratkan dengan variabel x. Karena masih mendapatkan kembalian 1.000 rupiah maka akan menjadi persamaan seperti dibawah ini:
4x + 1.000 = 5.000
4x = 5.000 – 1.000
4x = 4.000
x = 4.000/4
x = 1.000
Jadi harga satu penghapusnya ialah Rp 1.000.
Sekian penjelasan mengenai cara menyelesaikan persamaan linear satu variabel beserta contoh soal persamaan linear satu variabel. PLSV pada dasarnya memiliki cara pengerjaan yang hampir sama dengan PLDV. Hanya saja jumlah variabel di dalamnya yang berbeda. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.