10 Jenis Pola Bilangan Matematika Beserta Rumus dan Contohnya – Dalam ilmu Matematika terdapat materi pembelajaran mengenai pola bilangan. Isi materinya pun tergolong sangat mudah untuk dipahami oleh siswa. Biasanya rumus pola dalam bilangan beserta contoh pola bilangan matematika akan diajarkan di jenjang SMP. Lebih tepatnya ketika kita menginjak kelas 8 SMP hingga kelas 9. Namun tidak jarang pula materi tersebut diberikan ulang di jenjang SMA mengingat pentingnya mempelajari bilangan.
Kita sebagai siswa pun juga sering diberi tugas makalah pola bilangan matematika oleh guru maupun dosen. Sebenarnya apa pengertian pola dalam bilangan itu? Materi pola dalam sebuah bilangan ini mencakup beberapa hal penting seperti pola bilangan bertingkat, barisan bilangan, pola pembuktian rumus pola dalam bilangan segitiga dan masih banyak lagi. Berbagai jenis pola bilangan matematika beserta contohnya telah kita pelajari sejak menginjak bangku sekolah menengah pertama kelas 8. Materi pembelajaran Matematika ini diajarkan sebelum materi barisan geometri dan barisan aritmatika.
 |
| Pola Bilangan Matematika |
Materi pola dalam bilangan Matematika ini memang harus dipahami terlebih dahulu sebelum belajar mengenai barisan Matematika. Mengapa demikian? karena sedikit banyak pola tersebut berhubungan dengan geometri maupun aritmatika. Seperti yang sudah saya katakan di atas bahwa materi ini dapat digunakan sebagai pelengkap tugas makalah pola bilangan matematika kelas 8 hingga contohnya. Nah dalam pembahasan kali ini saya akan menjelaskan tentang beberapa jenis pola bilangan Matematika beserta rumus dan contohnya. Selain itu saya juga akan menjelaskan tentang pengertian pola dalam bilangan, barisan bilangan, pola bilangan bertingkat, pembuktian rumus pola bilangan segitiga dan hal hal yang berkaitan didalamnya.
10 Jenis Pola Bilangan Matematika Beserta Rumus dan Contohnya
Dalam ilmu Matematika kita mengenal adanya sebuah bilangan. Bilangan bilangan Matematika tersebut dapat dibagi menjadi beberapa jenis. Misalnya saja bilangan genap, bilangan ganjil, bilangan prima dan masih banyak lagi. Kemudian bilangan bilangan ini juga dapat dikumpulkan menjadi satu membentuk sebuah pola tertentu. Apa yang dimaksud pola bilangan itu?
Pengertian pola bilangan ialah pola tertentu yang terbentuk dari susunan beberapa bilangan. Susunan pola dalam bilangan ini akan terbentuk dari beberapa jenis himpunan bilangan. Contohnya dalam sebuah kalender terdapat tanggal 1 – 31. Angka 1 – 31 ini merupakan himpunan asli yang disusun menjadi pola yang bermula dari angka 1 sampai 31. Dengan demikian susunan pola dalam bilangannya akan menjadi 1, 2, 3, 4, 5 (minggu pertama) dan seterusnya. Susunan minggu pertama ini merupakan bentuk bilangan asli kurang dari 6. Masih banyak lagi jenis jenis pola bilangan dalam Matematika dengan berbagai rumusnya.
Adapula yang berpendapat bahwa pengertian pola bilangan sebagai sebuah pola yang disusun dari beberapa bilangan sehingga bentuknya teratur. Selain itu adapula yang mengartikannya sebagai aturan pemberlakuan bilangan secara urut. Dibawah ini terdapat penjelasan mengenai jenis jenis pola bilangan matematika, rumus rumusnya beserta contoh dan hal hal yang terdapat didalamnya seperti pembuktikan rumus pola bilangan segitiga, barisan bilangan dan sebagainya. Berikut penjelasan selengkapnya:
Baca juga : Konversi Satuan Berat (Ons, Pon, Kg, Ton dan Kwintal)
Pola Bilangan Ganjil
 |
| Gambar Pola dalam Bilangan Ganjil |
Jenis pola bilangan Matematika yang pertama ialah pola dalam bilangan ganjil. Bilangan ini akan membentuk susunan seperti gambar diatas. Dalam konteks kehidupan nyata pola tersebut sering kali digunakan untuk menguji logika kita semua. Materi bilangan ganjil ini sering kali muncul dalam berbagai tes seperti SBMPTN hingga ujian tulis lainnya. Gambar tersebut dapat dijabarkan menjadi beberapa keterangan didalamnya seperti di bawah ini:
- Bilangan ganjil akan membentuk pola 1, 3, 5, 7, 9, 11, . . .
- Barisan bilangan ganjilnya ialah 1, 3, 5, 7, 9, 11, . . .
- Deret bilangan ganjilnya ialah 1 + 3 + 5 + 7 + 9 + 11 + . . .
- Rumus pola bilangan suku ke n ialah Un = 2n – 1.
- Rumus jumlah n pada suku pertamanya ialah Sn = n².
Contoh Soal Pola Bilangan Ganjil
Diketahui susunan pola dalam bilangan yaitu 1, 3, 5, 7, . . . . Berapakah pola bilangan ganjil ke 20 nya? Jawabannya tidak lain adalah 39. Nah silahkan perhatikan cara menghitung deret bilangan ganjil di bawah.
Un = 2n – 1
U20 = 2 (20) – 1
= 40 -1
= 39
Pola Bilangan Genap
 |
| Gambar Pola dalam Bilangan Genap |
Jenis pola bilangan Matematika selanjutnya ialah pola dalam bilangan genap. Bilangan ini akan membentuk susunan pola seperti gambar diatas. Sama halnya seperti bilangan ganjil diatas, pada bilangan genap pun juga memiliki berbagai sifat serta manfaat. Gambar tersebut dapat dijabarkan menjadi beberapa keterangan didalamnya seperti di bawah ini:
- Bilangan genap akan membentuk pola 2, 4, 6, 8, 10, 12, . . .
- Barisan bilangan genapnya ialah 2, 4, 6, 8, 10, 12, . . .
- Deret bilangan genapnya ialah 2 + 4 + 6 + 8 + 10 + 12 + . . .
- Rumus pola bilangan suku ke n ialah Un = 2n.
- Rumus jumlah n pada suku pertamanya ialah Sn = n² + n.
Contoh Soal Pola Bilangan Genap
Diketahui susunan pola dalam bilangan yaitu 2, 4, 6, 8, . . . . Berapakah pola bilangan genap ke 20 nya? mudah saja. Jawabannya adalah 40 dengan perincian hitungan sebagai berikut:
Jawab.
Un = 2n
U20 = 2 (20)
= 40
Pola Bilangan Segitiga
 |
| Gambar Pola dalam Bilangan Segitiga |
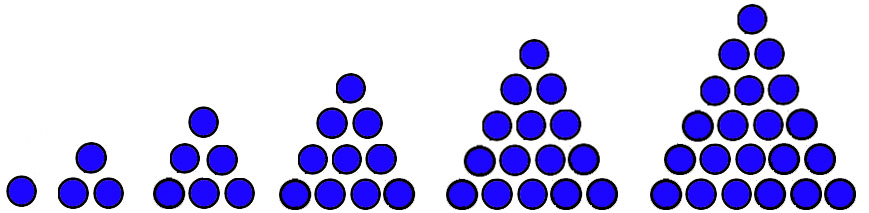
Jenis pola bilangan Matematika selanjutnya ialah pola dalam bilangan segitiga. Bilangan ini akan membentuk susunan pola seperti gambar diatas. Singkatnya bilangan akan disusun berbentuk seperti segitiga jika dilihat secara harfiah. Gambar tersebut dapat dijabarkan menjadi beberapa keterangan didalamnya seperti di bawah ini:
- Bilangan segitiga akan membentuk pola 1, 3, 6, 10, 15, 21, . . .
- Barisan bilangan segitiganya ialah 1, 3, 6, 10, 15, 21, . . .
- Deret bilangan segitiganya ialah 1 + 3 + 6 + 10 + 15 + 21 + . . .
- Rumus pola bilangan suku ke n ialah Un = ½ n (n + 1).
- Rumus jumlah n pada suku pertamanya ialah Sn = 1/6 n (n + 1)(n + 2).
Rumus pola bilangan segitiga ini dapat dibuktikan dengan beberapa susunan barisan bilangannya. Adapun pembuktian rumus pola bilangan segitiganya yaitu:
n ke 1 → 1 = ½ x 1 (1 + 1)
n ke 2 → 3 = ½ x 2 (2 + 1)
n ke 3 → 6 = ½ x 3 (3 + 1)
n ke 4 → 10 = ½ x 4 (4 + 1)
n ke 5 → 15 = ½ x 5 (5 + 1)
n ke 6 → 21 = ½ x 6 (6 + 1)
⋮
n = ½ n (n + 1)
Baca juga : Cara Menyelesaikan Persamaan Parabola Beserta Contoh Soal
Berdasarkan pembuktian rumus pola bilangan segitiga di atas, maka diperoleh rumus pola dalam bilangan segitiga yaitu:
Un = ½ n (n + 1)
Untuk pola bilangan segitiga ini hampir sama dengan pola dalam bilangan segilima dan segienam. Adapun rumus pola dalam bilangan segilima yaitu ½ n (3n + 1 ) dan rumus pola dalam bilangan segienam yaitu n (2n – 1). Jika kita buktikan dalam bentuk nilai, maka bilangan segitiga akan bernilai sama dengan nilai bilangan segilima maupun segienam. Nilai tersebut ialah 40755. 40577 terletak pada suku ke 285 bilangan segitiga, suku ke 165 bilangan segilima dan suku ke 143 bilangan segienam.
Catatan : Nilai 40755 ialah nilai pola bilangan segitiga sekaligus bilangan segilima dan bilangan segienam.
Contoh Soal Pola Bilangan Segitiga
Diketahui susunan pola dalam bilangan yaitu 1, 3, 6, 10, 15, . . . . Berapakah pola bilangan segitiga ke 20 nya? Jawabannya tidak lain adalah 190. Untuk bisa menghitungnya cukup perhatikan rumus di bawah:
Jawab.
Un = ½ n (n + 1)
U20 = ½(20) (20 + 1)
= 10 x 19
= 190
Pola Bilangan Persegi
 |
| Gambar Pola dalam Bilangan Persegi |
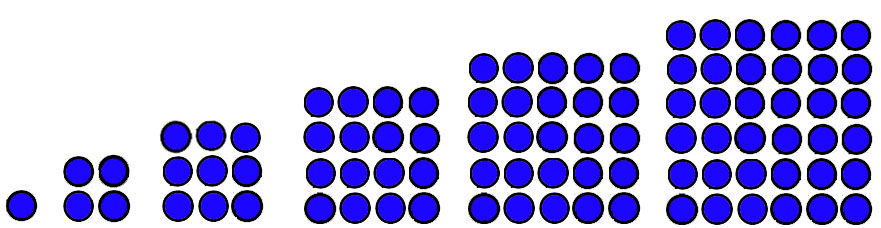
Jenis pola bilangan Matematika selanjutnya ialah pola dalam bilangan persegi. Bilangan tersebut memiliki urutan yang mudah dipahami karena bentuknya yang simpel. Gambar persegi diatas bisa kita jabarkan menjadi beberapa keterangan yang didalamnya memuat beberapa informasi, misalnya:
- Bilangan persegi akan membentuk pola 1, 4, 9, 16, 25, 36, . . .
- Barisan bilangan perseginya ialah 1, 4, 9, 16, 25, 36, . . .
- Deret bilangan perseginya ialah 1 + 4 + 9 + 16 + 25 + 36 + . . .
- Rumus pola bilangan suku ke n ialah Un = n².
- Rumus jumlah n pada suku pertamanya ialah Sn = 1/6 n (n + 1)(2n + 2).
Contoh Soal Pola Bilangan Persegi
Diketahui susunan pola dalam bilangan yaitu 1, 4, 9, 16, 25, . . . . Berapakah pola bilangan persegi ke 20 nya? Tentu saja jawabannya adalah 400. Lantas bagaimana cara menghitung bilangan tersebut? mudah saja, simaklah pembahasan di bawah.
Jawab:
Un = n²
U20 = 20²
= 400
Pola Bilangan Persegi Panjang
 |
| Gambar Pola dalam Bilangan Persegi Panjang |
Jenis pola bilangan matematika selanjutnya ialah pola dalam bilangan persegi panjang. Jenis bilangan diatas tentunya sangat mudah untuk dibaca dan dipahami mengingat bangun persegi panjang memiliki bentuk yang sederhana. Cara menghitungnya pun sama seperti cara kita menghitung pola bilangan persegi pada pembahasan sebelumnya. Kita bisa menjabarkan gambar diatas menjadi beberapa keterangan di bawah:
- Bilangan persegi panjang akan membentuk pola 2, 6, 12, 20, 30, 42, . . .
- Barisan bilangan persegi panjangnya ialah 2, 6, 12, 20, 30, 42, . . .
- Deret bilangan persegi panjangnya ialah 2 + 6 + 12 + 20 + 30 + 42 + . . .
- Rumus pola bilangan suku ke n ialah Un = n (n + 1).
- Rumus jumlah n pada suku pertamanya ialah Sn = 1/3 n (n + 1)(n + 2).
Contoh Soal Pola Bilangan Persegi Panjang
Diketahui susunan pola dalam bilangan yaitu 2, 6, 12, 20, 30, . . . . Berapakah pola bilangan persegi panjang ke 20 nya? tidak lain adalah 420. Kenapa bisa begitu? perhatikanlah rumus hitung matematika di bawah:
Jawab.
Un = n (n + 1)
U20 = 20 (20 + 1)
= 420
Pola Bilangan Segitiga Pascal
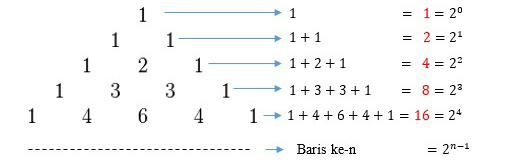
Jenis pola bilangan matematika selanjutnya ialah pola dalam bilangan segitiga pascal. Jenis pola ini memang berbeda dengan pola dalam bilangan lainnya. Hal ini dikarenakan susunan polanya berasal dari bilangan bilangan yang terdapat dalam segitiga pascal. Maka dari itu akan membentuk gambar pola seperti di bawah ini:
 |
| Gambar Pola dalam Bilangan Segitiga Pascal |
Berdasarkan gambar diatas, dapat kita peroleh rumus pola bilangan segitiga pascal yaitu Un = 2ⁿ⁻¹.
Pola Bilangan Fibonacci
 |
| Gambar Pola dalam Bilangan Fibonacci |
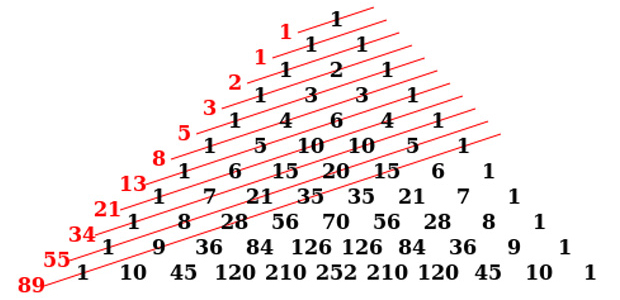
Jenis pola bilangan matematika selanjutnya ialah pola dalam bilangan fibonacci. Bilangan ini akan membentuk susunan pola seperti gambar diatas. Jika diperhatikan urutan bilangan tersebut terlihat sangat aneh karena cara menghitungnya ditarik sudutnya. Namun kita tidak perlu risau karena saya akan mengajarkan cara memahami gambar diatas. Gambar tersebut dapat dijabarkan menjadi beberapa keterangan didalamnya seperti di bawah ini:
- Bilangan fibonacci akan membentuk pola 1, 1, 2, 3, 5, 8, 13, . . .(Nilai 2 berasal dari hasil 1 + 1, nilai 3 berasal dari hasil 2 + 1, dan seterusnya).
- Rumus pola bilangan suku ke n ialah Un = Un – 1 + Un – 2.
Pola bilangan fibonacci ini merupakan bilangan yang membentuk pola yang asalnya dari jumlah bilangan setelahnya yaitu hasil dua bilangan sebelumnya yang dijumlahkan.
Pola Bilangan Pangkat Tiga
Jenis pola bilangan Matematika selanjutnya ialah pola dalam bilangan pangkat tiga. Pola ini terbentuk dari bilangan setelahnya yang merupakan hasil dari bilangan sebelumnya yang dipangkatkan tiga. Adapun contohnya yaitu:
2, 8, 512, 134.217.728, . . .
Keterangan:
Nilai 8 berasal dari 2³, 512 berasal dari 8³, 134.217.728 berasal dari 512³, dan seterusnya.
Baca juga : Merasionalkan Penyebut Pecahan Bentuk Akar Beserta Contoh
Pola Bilangan Aritmatika
 |
| Gambar Pola dalam Contoh Bilangan Aritmatika |
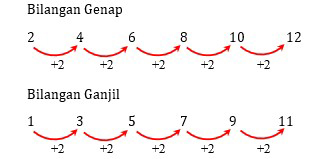
Jenis pola bilangan Matematika selanjutnya ialah pola dalam bilangan aritmatika. Pola dalam bilangan aritmatika ialah pola yang dibentuk dari bilangan sesudah dan sebelumnya dengan selisih yang sama. Bilangan ini akan membentuk susunan pola seperti gambar diatas. Gambar tersebut dapat dijabarkan menjadi beberapa keterangan didalamnya seperti di bawah ini:
- Contoh bilangan aritmatika akan membentuk pola 2, 4, 6, 8, 10, 12 (genap) atau 1, 3, 5, 7, 9, 11 (ganjil)
- Bilangan aritmatika termasuk dalam pola bilangan bertingkat.
- Bilangan aritmatika memiliki suku pertama yaitu U1 atau a, kemudian U2, U3, dan seterusnya.
- Bilangan aritmatika memiliki selisih atau beda yang dilambangkan dengan b. Maka nilai b = U2 – U1 dan seterusnya.
- Rumus pola bilangan aritmatika suku ke n ialah Un = a + (n – 1)b.
- Rumus jumlah n pada suku pertamanya ialah Sn = n/2 (a + Un) atau Sn = n/2 (2a + (n-1) b).
Pola Bilangan Geometri
 |
| Gambar Pola dalam Contoh Bilangan Geometri |
Jenis pola bilangan matematika selanjutnya terdapat pada bilangan geometri. Kita sering menemukannya dalam bentuk baris dan deret geometri. Materi tersebut bisa dibilang klasik dan sering kali kita temukan dalam berbagai jenjang pendidikan. Saya pun juga pernah membahas tentang rumus, pola, dan cara menghitung baris dan deret geometri dalam artikel sebelumnya.
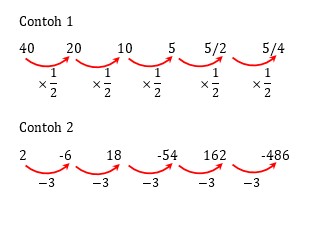
Pola dalam bilangan geometri ialah pola yang dibentuk dari perkalian bilangan sebelum dengan bilangan tertentu yang nilainya tetap. Bilangan ini akan membentuk susunan pola seperti gambar diatas. Gambar tersebut dapat dijabarkan menjadi beberapa keterangan didalamnya seperti di bawah ini:
- Contoh bilangan aritmatika akan membentuk pola 40, 20, 10, 5, 5/2, . . .
- Bilangan geometri termasuk dalam pola bilangan bertingkat.
- Bilangan geometri memiliki suku pertama yaitu U1 atau a, kemudian U2, U3, dan seterusnya.
- Bilangan geometri memiliki rasio yang dilambangkan dengan r. Maka nilai r = U2/U1 dan seterusnya.
- Rumus pola bilangan geometri suku ke n ialah
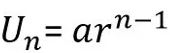
- Rumus jumlah n pada suku pertamanya ialah
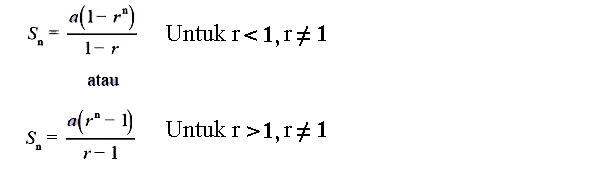
Sekian penjelasan mengenai jenis jenis pola bilangan Matematika beserta rumus dan contohnya. Materi pola dalam bilangan Matematika ini mencakup beberapa hal seperti barisan bilangan, pola dengan tipe bertingkat, pembuktian rumus pola bilangan segitiga dan sebagainya. Semoga artikel ini dapat bermanfaat untuk anda dan terimakasih sudah membaca materi pola bilangan matematika diatas.


Lumayan lah gak bisa dimengerti :v
Bagus
yang benar ditambah ato dikurang sih. masa 20+1=19
terimakasih atas infonya jangan lupa kunjungi blog saya ; posthigher.home.blog dan jangan lupa cek website kampus saya ; ppns.ac.id