Contoh Soal Pertidaksamaan Rasional atau Pecahan Lengkap – Dalam ilmu Matematika terdapat pembahasan mengenai pertidaksamaan rasional. Apa pengertian pertidaksamaan rasional itu? Apa saja jenis jenis pertidaksamaan rasional? Bagaimana cara menyelesaikan pertidaksamaan rasional? Pengertian pertidaksamaan secara umum ialah kalimat terbuka dalam Matematika yang memakai tanda kurang dari (<), lebih dari (>), kurang dari sama dengan (≤) dan lebih dari sama dengan (≥). Kemudian pertidaksamaan rasional dapat diartikan sebagai bentuk pertidaksamaan yang mengandung fungsi rasional sehingga pernyataan fungsi tersebut dapat berupa g(x) atau f(x) dengan ketentuan f(x) ≠ 0.
Sebelum mempelajari materi pertidaksamaan rasional tersebut, anda haus memahami pengertian pertidaksamaan rasional, jenis jenis pertidaksamaan rasional, dan cara mengerjakan contoh soal pertidaksamaan rasional terlebih dahulu. Pertidaksamaan memiliki konsep yang berhubungan dengan penyelesaian interval. Hal ini juga berlaku untuk pertidaksamaan rasional/pecahan maupun pertidaksamaan kuadrat. Kedua jenis pertidaksamaan tersebut memiliki persamaan dalam hal mencari hasil nilai HP (himpunan penyelesaian). Akan tetapi keduanya berbeda dalam hal ketentuan penyebut yang tidak sama dengan nol pada pertidaksamaan rasional/pecahan.
Jenis jenis pertidaksamaan rasional atau pecahan dapat diselesaikan menggunakan tanda hasil operasi pembagian atau perkalian bilangan, baik negatif maupun positif. Penentuan hasil tanda operasi pada pembagian atau perkalian bilangan sesuai dengan operasi tanda pada bilangannya. Hasilnya akan positif apabila tanda operasi pada dua bilangan bertandanya sama. Namun hasilnya akan negatif jika tandanya berbeda pada operasi dua bilangan bertanda. Pada kesempatan kali ini saya akan membagikan beberapa contoh soal pertidaksamaan rasional atau pecahan lengkap. Selain itu saya juga akan membahas pengertian pertidaksamaan rasional, cara menyelesaikan pertidaksamaan rasional dan materi pertidaksamaan rasional lainnya. Untuk lebih jelasnya dapat anda simak di bawah ini.
Contoh Soal Pertidaksamaan Rasional atau Pecahan Lengkap
Cara menyelesaikan pertidaksamaan rasional pada umumnya dapat dilakukan melalui penentuan akar (pembuat nol) disetiap faktor, penentuan interval dalam pertidaksamaan tersebut, pemfaktoran dan penentuan tanda interval melalui akar akar (pembuat nol) yang membatasinya. Materi pertidaksamaan rasional ini sering diajarkan ketika di bangku sekolah. Bahkan materi Matematika tersebut juga dijadikan sebagai bahan pembuat soal soal Ujian, baik Ujian Nasional maupun Ujian Sekolah. Apakah anda tahu apa saja sifat sifat pertidaksamaan rasional itu? Apa definisi pertidaksamaan rasional?
Baca juga : Rangkuman Soal Aplikasi Turunan Beserta Pembahasan Singkatnya
Sebelum membagikan contoh soal pertidaksamaan rasional tersebut. Saya akan menjelaskan terlebih dahulu mengenai pengertian pertidaksamaan rasional, jenis jenis pertidaksamaan rasional, sifat sifat pertidaksamaan rasional dan cara menyelesaikan pertidaksamaan rasional. Perhatikan contoh pertidaksamaan di bawah ini:
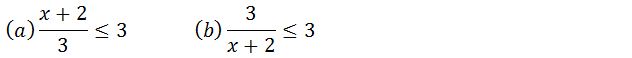
Dari pertidaksamaan di atas dapat kita lihat bahwa (a) bukan pertidaksamaan rasional dan (b) merupakan pertidaksamaan rasional/pecahan. Penyataan (a) bukan pertidaksamaan rasional karena variabel tidak termuat dalam penyebutnya. Sedangkan penyebut (b) memuat variabel sehingga termasuk dalan jenis pertidaksamaan rasional. Maka dari itulah pengertian pertidaksamaan rasional ialah jenis pertidaksamaan yang mengandung variabel pada penyebutnya dan berbentuk rasional atau pecahan.
Jenis Jenis Pertidaksamaan Rasional
Pertidaksamaan rasional secara umum dapat dibagi menjadi dua jenis yaitu pertidaksamaan rasional kuadrat dan pertidaksamaan rasional linear. Bentuk umum pertidaksamaan tersebut berbeda beda. Adapun bentuk umumnya yaitu sebagai berikut:
Pertidaksamaan Rasional Linear
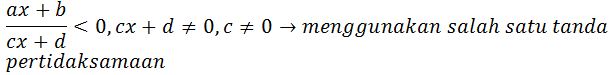
Pertidaksamaan Rasional Kuadrat
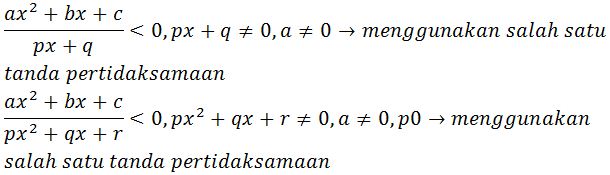
Baca juga : Cara Menghitung Besar Sudut Bangun Datar dan Contoh Soalnya
Sifat Sifat Pertidaksamaan Rasional
Setelah membahas tentang pengertian pertidaksamaan rasional dan jenis jenis pertidaksamaan rasional tersebut. Kemudian saya akan menjelaskan tentang sifat fifat pertidaksamaan rasional dalam materi pertidaksamaan rasional Matematika tersebut. Sifat sifat ini dapat anda gunakan untuk menyelesaikan contoh soal pertidaksamaan rasional yang tersedia. Adapun sifat sifat dalam pertidaksamaan rasional yaitu sebagai berikut:
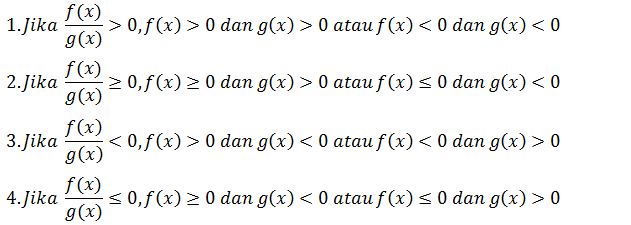
Cara Menyelesaikan Pertidaksamaan Rasional
Apakah anda tahu bagaimana cara menyelesaikan contoh soal pertidaksamaan rasional itu? Dalam materi pertidaksamaan rasional atau pecahan ini terdapat beberapa langkah yang digunakan dalam penyelesaian pertidaksamaan rasional. Pertidaksamaan pecahan dapat diselesaikan menggunakan beberapa langkah seperti di bawah ini yaitu:
- Seluruh suku dipindahkan ke dalam satu ruas yang sama, baik ruas kanan atau kiri sehingga salah satu ruasnya hanya tersisa nol. Namun antar ruasnya tidak diperbolehkan untuk mengalikan silang pembilang ataupun penyebutnya. Hal ini dikarenakan bentuk pertidaksamaan dapat berubah jika perkalian silang dilakukan.
- Melakukan operasi aljabar agar bentuknya berubah menjadi lebih sederhana. Kemudian nilai x dapat diperoleh melalui pemfaktoran yang dilakukan.
- Kemudian nilai x dapat disusun dalam garis bilangan yang tersedia. Namun setiap daerah pada pertidaksamaan pangkat besar ataupun tinggi harus ditentukan tandanya terlebih dahulu secara manual. Caranya yaitu salah satu nilai x dalam daerah tadi diambil dan setelah itu hasilnya diuji menggunakan bentuk pertidaksamaan yang tersedia.
Baca juga : Contoh Soal SPLDV Pecahan Beserta Jawabannya Lengkap
Contoh Soal Pertidaksamaan Rasional
Agar anda lebih paham mengenai pengertian pertidaksamaan rasional, jenis jenis pertidaksamaan rasional dan sifat sifat pertidaksamaan rasional di atas. Saya akan membagikan beberapa contoh soal materi pertidaksamaan rasional. Adapun contoh dan pembahasannya yaitu sebagai berikut:
1. Tentukan pertidaksamaan berikut 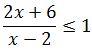 !
!
Jawab.
Pertidaksamaan rasional di atas dapat dinyatakan menggunakan bentuk umum seperti di bawah ini:

Pertidaksamaan di atas memiliki nilai sama dengan nol atau negatif sehingga berlaku persamaan seperti di bawah ini:
{x + 8 ≤ 0 dan x – 2 > 0} atau {x + 8 ≥ 0 dan x – 2 < 0}
⇔{x ≤ -8 dan x > 2} atau {x ≥ -8 dan x < 2}
Setelah daerah tersebut ditentukan irisannya, maka bentuk yang diperoleh akan menjadi seperti berikut ini:
⇔ Ø atau -8 ≤ x < 2
⇔ -8 ≤ x < 2
Jadi himpunan penyelesaian pertidaksamaan 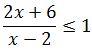 adalah -8 ≤ x < 2.
adalah -8 ≤ x < 2.
2. Tentukan pertidaksamaan berikut ![]() !
!
Jawab.
Contoh soal pertidaksamaan rasional di atas dapat dinyatakan menggunakan bentuk umum seperti di bawah ini:

Pertidaksamaan di atas memiliki hasil nilai tidak sama dengan nol atau positif sehingga berlaku persamaan seperti di bawah ini:
{-2x – 6 > 0 dan x + 4 > 0} atau {-2x – 6 < 0 dan x + 4 < 0}
⇔{-2x > 6 dan x > -4} atau {-2x < 6 dan x < -4}
⇔{x < -3 dan x > -4} atau {x > -3 dan x < -4}
⇔-4 < x < -3 atau Ø
⇔-4 < x < -3
Jadi himpunan penyelesaian pertidaksamaan ![]() ialah -4 < x < -3.
ialah -4 < x < -3.
Inilah beberapa contoh soal pertidaksamaan rasional atau pecahan lengkap. Pengertian pertidaksamaan rasional ialah bentuk pertidaksamaan yang mengandung fungsi rasional sehingga pernyataan fungsi tersebut dapat berupa g(x) atau f(x) dengan ketentuan f(x) ≠ 0. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi pertidaksamaan rasional di atas.