Menentukan Interval Fungsi Naik dan Fungsi Turun Beserta Contoh Soal – Interval dianggap salah satu materi matematika yang cukup meyulitkan. Tak sedikit siswa gagal ketika diminta mengerjakan soal karena tak mengetahui rumus interval fungsi naik dan turun. Kita tahu bahwa dalam grafik f pada titik x terdapat garis singgung yang miring karena turunan f'(x) pertama. Untuk itu garis singgung akan naik apabila f'(x) > 0. Sedangkan garis singgung akan turun apabila f'(x) < 0. Hal ini juga berhubungan dengan kenyataan bahwa m = f'(x).
Dari ketentuan tersebut muncul teori dalam ketentuan sebuah fungsi yang sedang mengalami kemonotonan seperti menentukan fungsi naik dan fungsi turun. Cara menghitung interval fungsi naik dan fungsi turun tidak boleh sembarangan karena kita harus berlandaskan syarat internal fungsi yang berlaku. Inilah alasan mengapa keduanya memiliki selisih interval yang tidak jauh berbeda meskipun dalam kategori naik maupun turun.
Ketika mempelajari ilmu matematika sendiri kita akan disuguhkan dua jenis fungsi berbeda karakteristik yakni fungsi naik dan turun. Ada kalanya sebuah fungsi interval bisa dinyatakan naik maupun sebaliknya tanpa ada ikatan waktu. Jadi sewaktu-waktu perubahan dapat terjadi dan hal inilah yang membuat siswa merasa kesulitan untuk melakukan analisa.
Menentukan Interval Fungsi Naik dan Fungsi Turun Beserta Contoh Soal
Sebelum masuk membahas lebih dalam materi interval fungsi naik dan fungsi turun. Sebaiknya anda memahami terlebih dahulu mengenai pengertian fungsi naik dan pengertian fungsi turun. Dalam selang tertentu fungsi f dapat dinyatakan naik apabila bilangan x1 dan x2 atau sembarang dua memiliki besar x1 < x2 sehingga nilai f(x1) < f(x2).
Kemudian dalam selang tertentu fungsi f dapat dinyatakan turun apabila bilangan x1 dan x2 atau sembarang dua memiliki besar x1 > x2 sehingga nilai f(x1) > f(x2). Pada kesempatan kali ini saya akan menjelaskan tentang cara menentukan interval fungsi naik dan fungsi turun beserta contoh soal interval fungsi naik dan fungsi turun.
Apabila gerakan x ke arah kanan, maka fungsi akan dinyatakan naik sehingga gerakan grafik fungsi menuju ke atas. Sedangkan gerakan grafik fungsi akan menuju ke bawah jika fungsinya turun. Misalnya saja pada selang terdapat fungsi yang naik dari samping (-∞, a), maka pada selang (a, b) akan tetap konstan dan pada selang (b, ∞) akan turun. Dalam hal ini berlaku konsep materi fungsi naik dan turun bahwa sebuah fungsi akan naik jika turunannya positif dan akan turun fungsinya jika turunannya negatif. Sedangkan dalam selang tersebut, fungsi akan konstan jika seluruh selangnya memiliki turunan nol.
Baca juga : Contoh Soal Perbandingan Trigonometri pada Segitiga Siku Siku Lengkap
Rumus Interval Fungsi Naik dan Turun
Cara menentukan interval fungsi naik dan turun dapat dilakukan dengan mudah. Cara menentukan fungsi naik pada f(x) dapat dilakukan melalui pertidaksamaan f'(x) > 0 yang diselesaikan terlebih dahulu. Hal ini juga berlaku untuk cara menentukan fungsi turun pada f(x) yang dilakukan melalui pertidaksamaan f'(x) yang diselesaikan.
Di bawah ini terdapat beberapa ketentuan cara menentukan interval fungsi naik dan fungsi turun dalam Matematika. Kita bisa menjumpainya di buku pedoman matematika tingkat SMA maupun SMK secara lengkap. Tapi untuk mempersingkat waktu saya akan menjabarkannya pada poin-poin berikut:
- Apabila f'(x) > 0 maka fungsi f(x) dinyatakan naik.
- Apabila f'(x) < 0 maka fungsi f(x) dinyatakan turun.
- Apabila f'(x) = 0 maka fungsi f(x) dinyatakan stasioner.
- Apabila f'(x) ≤ 0 maka fungsi f(x) dinyatakan tidak naik.
- Apabila f'(x) ≥ 0 maka fungsi f(x) dinyatakan tidak turun.
Agar lebih paham lagi mengenai maksud materi interval fungsi naik dan fungsi turun tersebut, maka anda dapat memperhatikan grafik di bawah ini:
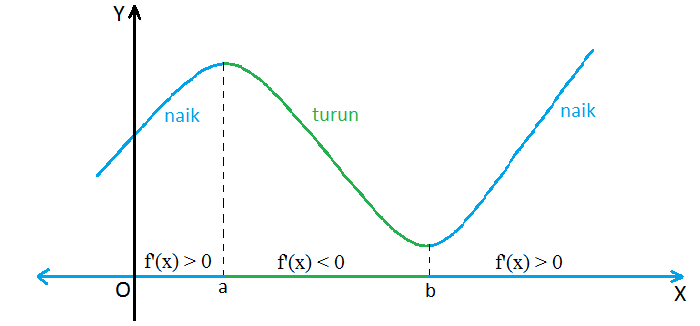
Berdasarkan grafik di atas dapat dilihat bahwa interval x < a atau x > b terdapat pada fungsi naik dan interval a > x < b terdapat pada fungsi turun. Materi fungsi naik dan turun tidak hanya dilihat melalui grafik atau visual saja. Namun dapat pula ditentukan fungsinya melalui turunan pertama dari fungsi tersebut. Untuk itu berlaku ketentuan seperti di bawah ini:
- Pada I terdapat f naik apabila di Interval I semua x nya memiliki besar f'(x) > 0.
- Pada I terdapat f turun apabila di Interval I semua x nya memiliki besar f'(x) < 0.
Baca juga : Rumus Trigonometri Kelas 10 Beserta Contoh Soal
Contoh Soal Interval Fungsi
Agar anda lebih paham mengenai cara menentukan interval fungsi naik dan fungsi turun di atas. Maka saya akan membagikan contoh soal interval fungsi naik dan fungsi turun yaitu sebagai berikut:
1. Tentukan interval f(x) naik dan turun apabila f(x) = x² – 4x + 6?
Jawab.
Langkah pertama ialah menentukan turunan pertama dari f(x) = x² – 4x + 6. Maka hasilnya menjadi:
f'(x) = 2x – 4
Kemudian menentukan fungsi naik menggunakan ketentuan diatas, sehingga:
f(x) naik → f'(x) > 0
2x – 4 > 0
2x > 4
x > 2
Setelah itu menentukan fungsi turunnya menggunakan cara di bawah ini:
f(x) turun→ f'(x) < 0
2x – 4 < 0
2x < 4
x < 2
Jadi f(x) naik dalam interval x > 2 dan turun dalam interval x < 2.
2. Tentukan interval f(x) naik apabila f(x) = 4x³ – 12x² – 36x ?
Jawab.
Cara menentukan interval fungsi naik yang pertama ialah menentukan turunan pertama dari f(x) terlebih dahulu. Maka:
f'(x) = 12x² – 24x – 36
Baca juga : Contoh Soal Pertidaksamaan Rasional atau Pecahan Lengkap
Kemudian menentukan interval fungsi naik dan fungsi turun, dimana fungsi naik berlaku f'(x) > 0 sehingga menjadi 12x² – 24x – 36 > 0. Hasil ini kemudian diubah menjadi persamaan sama dengan nol, sehingga:
12x² – 24x – 36 = 0
x² – 2x – 3 = 0
(x – 3)(x + 1) = 0
x = 3 atau x = -1

Jadi f(x) naik dalam interval x < -1 atau x > 3.
3. Diketahui f(x) = 1/3 x³ – 3x² – 7x + 8. Tentukan internal supaya kurva y = f(x) naik dan kurva y = f(x) turun?
Jawab.
Contoh soal fungsi naik dan fungsi turun di atas dapat dicari dengan cara menentukan turunan pertama f(x) terlebih dahulu. Maka hasilnya:
f'(x) = x² – 6x – 7
Fungsi naik memiliki syarat f'(x) > 0, sehingga:
f'(x) > 0
x² – 6x – 7 > 0
(x + 1)(x – 7) > 0
x + 1 = 0 atau x – 7 = 0
x = -1 atau x = 7
Interval x memiliki kurva naik apabila x < -1 atau x > 7.
Fungsi turun memiliki syarat f'(x) < 0, sehingga:
f'(x) < 0
x² – 6x – 7 < 0
(x + 1)(x – 7) < 0
x + 1 = 0 atau x – 7 = 0
x = -1 atau x = 7
Interval x memiliki kurva turun apabila -1 < x < 7.
Sekian penjelasan mengenai cara menentukan interval fungsi naik dan fungsi turun beserta contoh soal interval fungsi naik dan fungsi turun. Interval fungsi dapat dinyatakan naik apabila f'(x) > 0 dan turun apabila f'(x) < 0. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.