Cara Menentukan Gradien Garis Beserta Rumus dan Contohnya – Dalam pelajaran Matematika terdapat pembahasan mengenai materi gradien. Materi ini sering dikaitkan dengan adanya persamaan garis lurus. Rumus gradien garis pun akhirnya jadi materi wajib bagi siswa yang duduk di bangku SMP. Menariknya, ketika menginjak materi gradien maka kita akan menjumpai satu dan dua variabel.
Seperti yang telah kita ketahui bahwa persamaan garis lurus dapat dikaitkan dengan materi gradien. Bagaimana cara menentukan gradien garis itu? Seperti yang telah kita ketahui bahwa persamaan garis lurus ialah persamaan yang menjelaskan tentang persamaan dalam suatu garis lurus. Persamaan ini memiliki karakteristik berupa pangkat tertinggi yang dimiliki oleh variabelnya. Dalam satu garis lurus terdapat jumlah titik titik yang tak terhingga sampai dikumpulkan dan saling berdampingan. Hal inilah yang menyebabkan adanya gradien. Untuk itulah terbentuk rumus gradien pada persamaan garis dan contoh soal gradien.
Seperti yang telah kita ketahui bahwa sebuah garis lurus dapat dijelaskan melalui persamaan. Pernyataan satu garis lurus dapat berupa satu atau lebih persamaan. Kemudian adapula pengertian gradien yaitu nilai yang menggambarkan kemiringan pada sebuah garis. Cara mencari gradien pada persamaan garis dapat dilakukan dengan beberapa metode. Metode penyelesaiannya tersebut disesuaikan dengan informasi soal yang diketahui. Nah pada kesempatan kali ini saya akan menjelaskan tentang cara menentukan gradien garis beserta rumus gradien pada persamaan garis. Selain itu saya juga akan membagikan contoh soal gradien persamaan garisnya. Untuk lebih jelasnya dapat anda simak di bawah ini.
Cara Menentukan Gradien Garis Beserta Rumus dan Contohnya
Cara mencari gradien pada persamaan garis pada umumnya menggunakan prinsip yang sama. Sebelum menjelaskan tentang rumus gradien tersebut. Saya akan menjelaskan tentang pengertian gradien terlebih dahulu. Dalam sebuah garis terdapat pernyataan nilai gradien yang dijelaskan dalam bentuk perbandingan satuan horizontal (x) dengan satuan vertikal (y). Nilai gradien yang terdapat dalam garis lurus sama dengan 0 ketika sejajar dengan sumbu x. Sedangkan nilai gradien yang terdapat dalam garis lurus sama dengan tidak dapat ditentukan/tak hingga (∞) ketika sejajar dengan sumbu y. Perhatikan gambar di bawah ini:
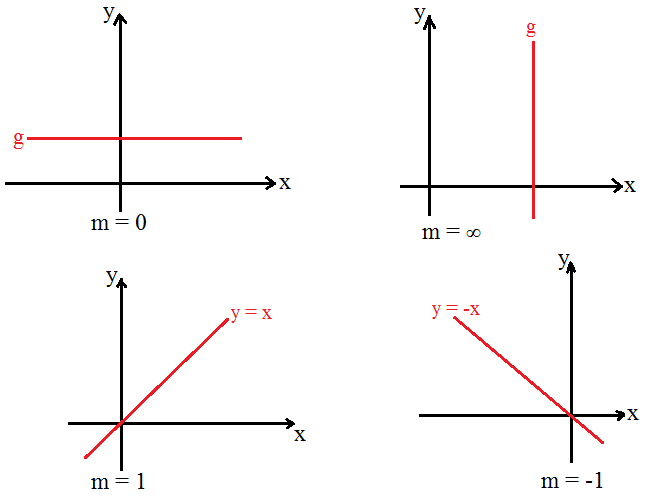
Nilai gradien akan sama dengan 1, jika persamaan garisnya y = x. Sedangkan gradien akan bernilai sama dengan -1, jika persamaan garisnya y = -x. Bagaimana cara menentukan gradien garis itu? Cara memperoleh nilai gradien dapat dilakukan dengan beberapa metode. Untuk metode pencarian ini memperhatikan perbandingan sumbu x dengan y dan letak garisnya. Di bawah ini terdapat penjelasan mengenai cara mencari gradien pada persamaan garis yaitu sebagai berikut:
Baca juga : Kumpulan Soal Integral Tentu Beserta Pembahasannya Lengkap
Menentuan Gradien dari Gambar
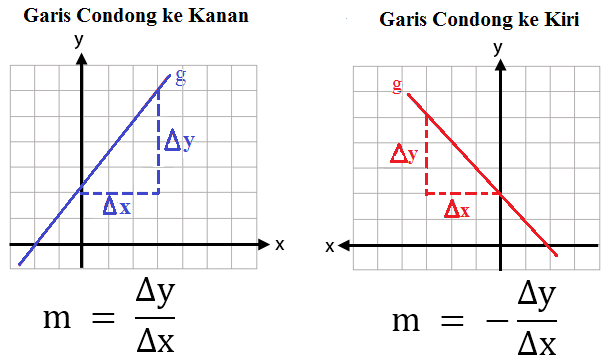
Cara menghitung gradien pada persamaan garis yang pertama dapat dilakukan melalui gambarnya. Penentuan gradien dari gambar ini dilakukan dengan memperhatikan perbandingan nilai sumbu x dengan sumbu y dan posisi garis itu sendiri. Adapun ketentuannya yaitu sebagai berikut:
- Gradien akan bernilai positif (+) apabila garisnya condong ke arah kanan.
- Gradien akan bernilai negatif apabila garisnya condong ke arah kiri.
Perhitungan besar gradien berasal dari perbandingan sumbu x dan sumbu y nya. Untuk lebih jelasnya dapat anda perhatikan gambar di bawah ini:
Menentukan Gradien dari Persamaan y = mx + c
Cara menentukan gradien garis selanjutnya dapat melalui persamaan y = mx + c. Nilai gradien yang dimiliki sama dengan m jika diketahui persamaan y = mx + c. Selain itu gradien juga memiliki besar berupa bilamgan di depan x atau koefisien x, dimana tandanya dapat berupa negatif ataupun positif. Apabila garisnya memiliki gambar yang condong ke kanan, maka gradiennya bernilai positif. Sedangkan apabila garisnya memiliki gambar yang condong ke kiri, maka gradiennya bernilai negatif.
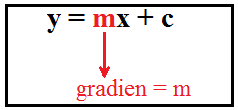
Menentukan Gradien dari Persamaan ax + by + c = 0
Cara mencari gradien dari persamaan garis selanjutnya dapat melalui persamaan ax + by + c = 0. Persamaan garis berbentuk ax + by + c = 0 dapat digunakan untuk mencari nilai gradien dengan cara membandingkan koefisien y dengan koefisien x, dimana perbandingannya memiliki tanda negatif. Kita dapat melihat kecondongan garis seperti halnya dalam persamaan y = mx + c sehingga hasil gradiennya yang dilihat. Garis akan condong ke arah kanan apabila gradiennya bernilai positif. Sedangkan garis akan condong ke arah kiri apabila gradiennya bernilai negatif. Adapun rumus gradien dalam garis yang persamaannya ax + by + c = 0 yaitu sebagai berikut:

Baca juga : Rumus Limit Tak Hingga Beserta Contoh Soal Lengkap
Menentukan Gradien Melalui Dua Titik Diketahui
Cara menentukan gradien garis selanjutnya ialah melalui dua titik yang telah diketahui. Dalam contoh soal gradien biasanya terdapat sebuah garis yang melalui dua buah titik. Dua titik ini digunakan untuk mengetahui besar gradien yang akan dicari. Contohnya sebuah garis dilalui oleh dua buah titik seperti titik A (x1, y1) dan titik B (x2, y2). Adapun rumus gradien yang dapat digunakan yaitu sebagai berikut:

Sifat Sifat Gradien pada Dua Garis
Setelah menjelaskan tentang cara mencari gradien pada persamaan garis di atas. Selanjutnya saya akan membahas tentang sifat sifat gradien pada dua buah garis. Kedudukan dua garis pada umumnya dapat dibagi menjadi dua macam yaitu dua garis saling tegak lurus dan saling sejajar. Kedua garis yang saling melakukan hubungan akan menghasilkan nilai hubungan gradien pada kedua garis itu sendiri.
Dua Garis Saling Sejajar
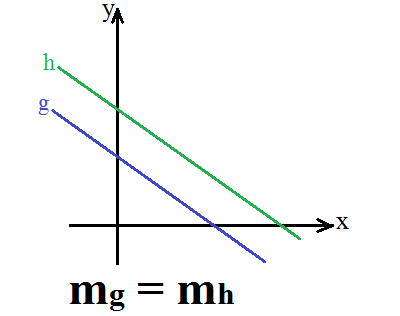
Dua garis sejajar memiliki hubungan gradien yang nilainya sama. Contoh dua garis diketahui saling sejajar seperti garis g dan garis h. Kedua garis tadi memiliki nilai gradien yang berhubungan yaitu mg = mh. Untuk lebih jelasnya perhatikan gambar di bawah ini:
Dua Garis Saling Tegak Lurus
Dua garis saling tegak lurus memiliki nilai gradien yang saling berhubungan jika berkebalikan dengan gradien pada garis lainnya, Selain itu gradiennya memiliki nilai yang dikalikan dengan -1. Contohnya dua garis saling tegak lurus yaitu garis g dan h, dimana kedua garis ini memiliki nilai gradien yang berhubungan seperti mg x mh = -1. Untuk lebih jelasnya dapat anda simak gambar di bawah ini:
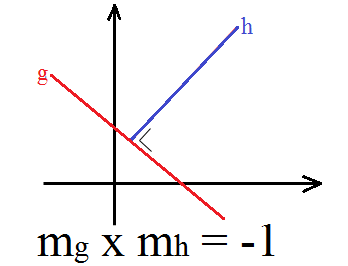
Agar anda lebih memahami mengenai cara menentukan gradien garis tersebut. Maka saya akan membagikan contoh soal gradien terkait rumus gradien pada persamaan garis di atas. Adapun contoh soal dan pembahasannya yaitu sebagai berikut:
Diketahui sebuah garis melewati titik A(2, 4) dan B(6, 8). Hitunglah gradiennya?
Jawab.
Untuk mencari gradien pada persamaan garis yang melalui titik A(2, 4) dan B(6, 8) tersebut dapat menggunakan rumus di bawah ini:

Jadi gradien garis tersebut ialah 1.
Demikianlah penjelasan mengenai cara menentukan gradien garis beserta rumus gradien pada persamaan garis. Pengertian gradien ialah nilai yang menggambarkan kemiringan pada sebuah garis. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.


