Materi Hiperbola Matematika Beserta Rumus dan Contoh Soal – Dalam pelajaran Matematika tentunya terdapat materi pembelajaran tentang irisan kerucut. Materi Matematika ini dapat dibagi menjadi beberapa pembelajaran lainnya seperti Hiperbola, Elips, Parabola dan Lingkaran. Setiap materi irisan kerucut memiliki pembahasan yang berbeda beda, baik rumus yang digunakan ataupun cara menyelesaikan contoh soalnya.
Salah satu materi ini yang sering dianggap sulit untuk beberapa orang ialah materi tentang hiperbola. Apakah anda tahu bagaimana persamaan hiperbola itu? Bagaimana rumus hiperbola itu? Bagaimana cara menyelesaikan contoh soal hiperbola? Sebelum memahami lebih lanjut mengenai materi tersebut, anda harus mengetahui terlebih dahulu tentang pengertian hiperbola itu.
Materi hiperbola Matematika merupakan salah satu materi irisan kerucut yang tidak kalah penting untuk dipelajari. Setiap siswa kesulitan untuk menyelesaikan soal soal irisan kerucut karena sulit untuk membedakan tentang hiperbola, parabola, elips, dan lingkaran.
Meski dianggap sulit, namun sebenarnya kita dapat menggunakan rumus yang tersedia untuk menyelesaikan soal soal terkait. Seperti halnya rumus hiperbola dan persamaan hiperbola yang digunakan untuk menyelesaikan contoh soal hiperbola yang tersedia. Dengan memahami rumus tersebut, anda dapat menyelesaikan soal soal tersebut. Apakah anda tahu apa pengertian hiperbola Matematika itu?
Materi Hiperbola Matematika Beserta Rumus dan Contoh Soal
Seperti yang telah saya jelaskan di atas bahwa pengertian hiperbola ialah kedudukan titik titik yang jaraknya selisih selalu tetap antara dua titik tertentu. Kedua titik ini bernama titik fokus. Hiperbola Matematika pada umumnya dapat dibagi menjadi dua jenis yaitu hiperbola vertikal dan hiperbola horizontal. Kedua macam hiperbola ini memiliki persamaan, rumus dan cara menyelesaikan contoh soal yang berbeda beda.
Baca juga : Rumus Modus Data Tunggal dan Kelompok Beserta Contoh Soal
Persamaan hiperbola jenis vertikal dan horizontal pada umumnya berbeda. Untuk itu rumus hiperbola yang digunakan untuk menyelesaikan contoh soal hiperbola nya juga berbeda. Hiperbola memang dapat dibagi menjadi dua jenis yaitu hiperbola vertikal dan hiperbola horizontal. Selain itu kedua hiperbola ini masih dapat dibagi lagi menjadi beberapa macam berdasarkan pusat O(0,0) dan pusat M(p,q).
Pada kesempatan kali ini saya akan menjelaskan tentang materi hiperbola Matematika beserta rumus hiperbola dan contoh soal hiperbola. Untuk lebih jelasnya dapat anda simak di bawah ini.
Hiperbola Horizontal Pusat O(0,0)
Pengertian hiperbola ialah himpunan pada seluruh titik yang jaraknya sama dengan selisih dua titik tertentu. Kedua titik tertentu ini dinamakan dengan titik api atau titik fokus hiperbola. Jarak yang selisihnya sama ialah 2a, dimana a > 0. Sedangkan jarak antara dua fokusnya dapat berupa 2c, dimana 2c > 2a.
Dalam sebuah persamaan hiperbola terdapat beberapa unsur tertentu seperti titik fokus, sumbu simetri, sumbu imajiner, eksentrisitas, titik pusat, panjang latus rectum, titik puncak, sumbu nyata dan persamaan direktris. Kita akan coba membahasnya satu persatu dimulai dari jenis hiperbola pertama yakni hiperbola horizontal dengan pusat O(0,0). Hiperbola ini memiliki bentuk umum seperti di bawah ini:
Rumus hiperbola horizontal pusat O(0,0) di atas termasuk dalam bentuk umum di dalamnya. Agar anda lebih paham mengenai materi ini, maka perhatikan grafik hiperbola horizontal pusat O(0,0) di bawah ini:
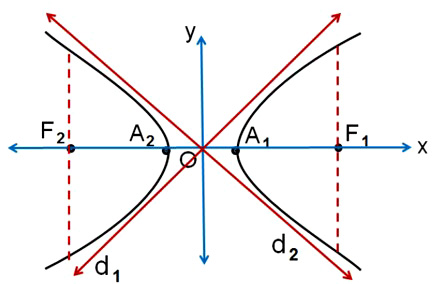
Grafik hiperbola horizontal pusat O(0,0) di atas memiliki beberapa unsur di dalamnya. Unsur tersebutlah yang berperan penting dalam persamaan hiperbola horizontal pusat O(0,0). Berikut unsur unsur materi hiperbola horizontal pusat O(0,0) yaitu:
- Memiliki titik puncak yang koordinatnya di A1(a,0) dan A2(-a,0).
- Memiliki sumbu sekawan di sumbu Y dan sumbu utama di sumbu X.
- Memiliki titik fokus berupa F1(c,0) dan F2(-c,0), dimana c² = a² + b².
- Memiliki nilai eksentrisitas berupa e = c/a.
- Memiliki rumus persamaan garis asimtot berupa
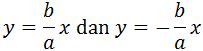 .
. - Memiliki panjang latus rectum yang rumusnya
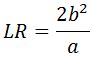 .
.
Hiperbola Vertikal Pusat O(0,0)
Jenis hiperbola selanjutnya ialah hiperbola vertikal dengan pusat O(0,0). Dari namanya saja kita sudah pasti bisa menebak bahwa jenis hiperbola satu ini memiliki sifat yang berkebalikan dari sebelumnya. Hiperbola vertikal memiliki bentuk umum seperti di bawah ini:
Baca juga : Materi Geometri Bidang Datar Kelas 12 SMA Lengkap
Rumus hiperbola vertikal pusat O(0,0) di atas termasuk dalam bentuk umum di dalamnya. Agar anda lebih paham mengenai materi ini, maka perhatikan grafik hiperbola vertikal pusat O(0,0) di bawah ini:
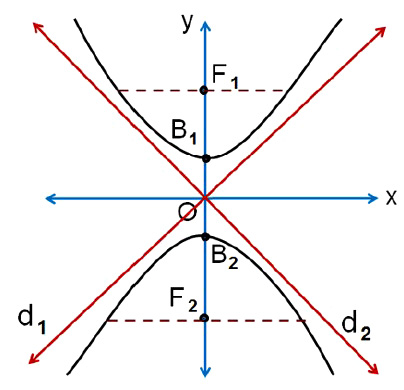
Grafik hiperbola vertikal pusat O(0,0) di atas memiliki beberapa unsur di dalamnya. Unsur tersebutlah yang berperan penting dalam persamaan hiperbola vertikal pusat O(0,0). Berikut unsur unsur materi hiperbola vertikal pusat O(0,0) yaitu:
- Memiliki titik puncak yang koordinatnya di B1(0,b) dan B2(0,-b).
- Memiliki sumbu sekawan di sumbu X dan sumbu utama di sumbu Y.
- Memiliki titik fokus berupa F1(0,c) dan F2(0,-c), dimana c² = a² + b².
- Memiliki nilai eksentrisitas berupa e = c/b.
- Memiliki rumus persamaan garis asimtot berupa
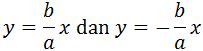 .
. - Memiliki panjang latus rectum yang rumusnya
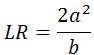 .
.
Hiperbola Horizontal Pusat M(p,q)
Selain mengandalkan kordinat kartesius ternyata kita juga bisa membuat hiperbola horizontal dengan titik pusat M. Pusat M mengacu pada titik di mana kedua cabang hiperbola memotong satu sama lain. Jika sumbu-x adalah garis tengah hiperbola, maka koordinat titik M adalah (p,q), yang merupakan titik tengah dari persamaan hiperbola.
Jenis hiperbola selanjutnya ialah hiperbola horizontal dengan pusat M(p,q). Hiperbola ini memiliki bentuk umum seperti di bawah ini:
Rumus hiperbola horizontal pusat M(p,q) di atas termasuk dalam bentuk umum di dalamnya. Agar anda lebih paham mengenai materi ini, maka perhatikan grafik hiperbola horizontal pusat M(p,q) di bawah ini:
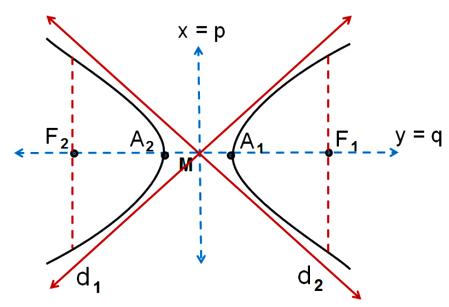
Grafik hiperbola horizontal pusat M(p,q) di atas memiliki beberapa unsur di dalamnya. Unsur tersebutlah yang berperan penting dalam persamaan hiperbola horizontal pusat M(p,q). Berikut unsur unsur materi hiperbola horizontal pusat M(p,q) yaitu:
- Memiliki titik puncak yang koordinatnya di A1(a + p,q) dan A2(-a + p,q).
- Memiliki sumbu sekawan di sumbu x = q dan sumbu utama di sumbu y = p.
- Memiliki titik fokus berupa F1(c + p, q) dan F2(–c + p, q), dimana c² = a² + b².
- Memiliki nilai eksentrisitas berupa e = c/a.
- Memiliki rumus persamaan garis asimtot berupa
 .
. - Memiliki panjang latus rectum yang rumusnya
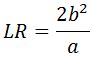 .
.
Baca juga : Contoh Soal Bangun Datar Gabungan Beserta Pembahasannya
Hiperbola Vertikal Pusat M(p,q)
Jenis hiperbola selanjutnya ialah hiperbola vertikal dengan pusat M(p,q). Hiperbola ini memiliki bentuk umum seperti di bawah ini:
Rumus hiperbola vertikal pusat M(p,q) di atas termasuk dalam bentuk umum di dalamnya. Agar anda lebih paham mengenai materi ini, maka perhatikan grafik hiperbola vertikal pusat M(p,q) di bawah ini:
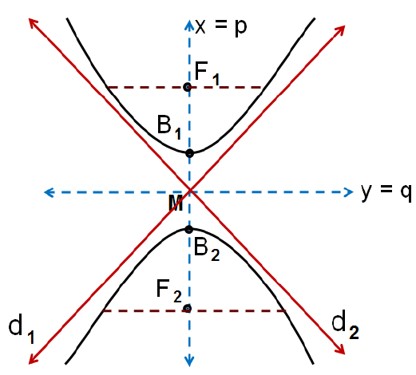
Grafik hiperbola vertikal pusat M(p,q) di atas memiliki beberapa unsur di dalamnya. Unsur tersebutlah yang berperan penting dalam persamaan hiperbola vertikal pusat M(p,q). Berikut unsur unsur materi hiperbola vertikal pusat M(p,q) yaitu:
- Memiliki titik puncak yang koordinatnya di B1(p,b + q), dan B2(p,–b + q).
- Memiliki sumbu sekawan di sumbu y = q dan sumbu utama di sumbu x = p.
- Memiliki titik fokus berupa F1(p,c + q) dan F2(p,–c + q), dimana c² = b² + a².
- Memiliki nilai eksentrisitas berupa e = c/b.
- Memiliki rumus persamaan garis asimtot berupa
 .
. - Memiliki panjang latus rectum yang rumusnya
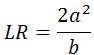 .
.
Contoh Soal Hiperbola
Setelah menjelaskan tentang rumus hiperbola, persamaan hiperbola dan pengertian hiperbola di atas. Selanjutnya saya akan membagikan contoh soal materi hiperbola Matematika tersebut. Berikut contoh soal dan pembahasannya:
Diketahui sebuah persamaan elips 36x² – 64y² = 144. Hitunglah titik fokus, eksentrisitas, titik puncak dan persamaan garis asimtot hiperbolanya?
Pembahasan.
Contoh soal hiperbola tersebut dapat diselesaikan dengan mudah menggunakan langkah langkah di bawah ini:
36x² – 64y² = 144
x²/64 – y²/36 = 1
a = 8 dan b = 6
Bentuk hiperbola maka akan jadi horizontal dan memiliki pusat O(0,0). Kemudian mencari nilai c menggunakan langkah di bawah ini:
c² = a² + b²
= 8² + 6²
= 64 + 36
= 100
c = √100
= 10
Materi hiperbola Matematika ini dapat dicari unsur unsurnya seperti di bawah ini:
- Titik puncaknya memiliki koordinat di A1(8,0) dan A2(-8,0).
- Titik fokusnya terdapat pada F1(10,0) dan F2(-10,0).
- Rumus persamaan garis asimtotnya dapat berupa y = 6/8 x dan y = -6/8 x.
- Nilai eksentrisitas hiperbolanya dapat berupa e = 10/8.
- Panjang latus Rectumnya ialah LR = 2.6²/8 = 72/8 = 9.
Demikianlah penjelasan mengenai materi hiperbola Matematika beserta rumus hiperbola dan contoh soal hiperbola. Pengertian hiperbola ialah kedudukan titik titik yang jaraknya selisih selalu tetap antara dua titik tertentu. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi tentang hiperbola di atas.