Contoh Soal Persamaan Kubik Beserta Cara Menyelesaikannya – Persamaan kubik ditemukan pertama kali saat dengan bentuk ax³ + bx² + cx + d = 0. Beberapa orang menganggap bahwa cara menyelesaikan persamaan kubik dapat dilakukan dengan metode yang rumit dan sulit. Namun sebenarnya cara menghitung persamaan kubik ini dapat dilakukan dengan mudah menggunakan karena telah ada sejak berabad abad lamanya.
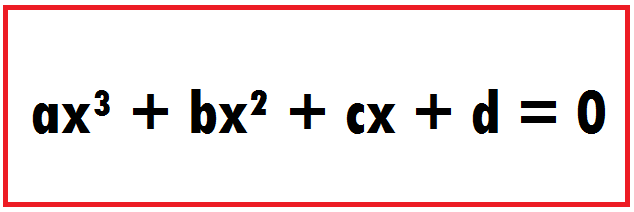
Bentuk persamaan kubik dinyatakan dalam ax³ + bx² + cx + d = 0. Apakah anda tahu bagaimana bentuk contoh soal persamaan kubik? Bagaimana cara menyelesaikan persamaan kubik? Persamaan kubik dalam aljabar mengandung satu variabel saja hingga memiliki bentuk umum seperti di atas.
Secara garis besar persamaan kubik bisa kita kerjakan menggunakan akar fungsi. Apabila persamaan kubik memiliki koefisien a, b, c, dan d, maka termasuk dalam bilangan riil karena akar yang ada di dalamnya merupakan nyata. Hal ini berlaku untuk semua jenis fungsi polinomial yang memiliki derajat ganjil. Dalam persamaan kubik ini terdapat beberapa cara yang digunakan untuk menentukan semua akarnya.
Contoh Soal Persamaan Kubik Beserta Cara Menyelesaikannya
Materi persamaan kubik dapat disebut dengan fungsi kubik atau fungsi pangkat tiga. Pengertian fungsi kubik ialah fungsi yang mempunyai persamaan yang bentuknya ax³ + bx² + cx + d = 0, dimana a ≠ 0. Persamaan kubik juga dapat diartikan sebagai sebuah polinomial yang memiliki orde tiga. Pada contoh soal persamaan kubik kalian akan menjumpai fungsi turunan yang berupa kuadrat. Kemudian fungsi kubik juga memiliki integral yang berbentuk fungsi kuartik (pangkat empat). Pada dasarnya koefisien a, b, c, dan d pada persamaan ini termasuk dalam bilangan riil.
Baca juga : Contoh Soal Domain Fungsi dan Cara Menentukan Lengkap
Seperti yang telah saya jelaskan di atas bahwa cara menyelesaikan persamaan kubik dapat dilakukan dengan beberapa metode. Setiap metode penyelesaian persamaan kubik memiliki kriteria pengerjaan yang berbeda beda. Sebelum membagikan tentang contoh soal persamaan kubik tersebut, saya akan membahas beberapa cara menghitung persamaan kubik seperti di bawah ini:
- Pemfaktoran
- Penyederhanaan Menjadi Persamaan Berbentuk Kuadrat
- Rumus Kubik
Pada kesempatan kali saya akan membagikan contoh soal persamaan kubik beserta cara menyelesaikan persamaan kubik. Untuk lebih jelasnya dapat anda simak di bawah ini.
Contoh Soal Persamaan Kubik
Rumus persamaan kubik dipakai untuk menyelesaikan contoh soal yang sulit. Dalam rumus tersebut terkandung metode aljabar yang berhubungan dengan akar n (radikal), empat koefisien dan empat operasi dasar dalam Aritmatika. Persamaan kubik dapat diselesaikan dengan menggunakan prinsip koefisien yang tidak harus sama dengan bidang yang dimilikinya.
Misalnya koefisien rasional yang terdapat dalam contoh soal persamaan kubik. Maka akar yang dimiliki bahkan tidak nyata atau termasuk dalam bilangan irasional yang kompleks. Agar anda lebih paham mengenai cara di atas, maka perhatikan contoh soal persamaan kubik di bawah ini:
1. Hitunglah himpunan penyelesaian dari persamaan x³ – x² – 4x = 0?
Jawab.
Untuk menyelesaikan persamaan kubik tersebut dapat diselesaikan dengan metode pemfaktoran seperti di bawah ini:
x³ – x² – 12x = 0
x(x² – x – 12) = 0
x(x- 4)(x + 3) = 0
x = 0 atau x = 4 atau x = -3
Jadi himpunan penyelesaian dari persamaan tersebut ialah {-3, 0, 4}.
2. Hitunglah himpunan penyelesaian dari persamaan x³ – 3x² – 4x + 12 = 0?
Jawab.
Contoh soal persamaan kubik tersebut dapat diselesaikan menggunakan metode pemfaktoran. Adapun cara menyelesaikan persamaan kubik menggunakan metode pemfaktoran yaitu:
x³ – 3x² – 4x + 12 = 0
x²(x – 3) – 4(x – 3) = 0
(x² – 4)(x – 3) = 0
(x + 2)(x – 2)(x – 3) = 0
x = -2 atau x = 2 atau x = 3
Jadi himpunan penyelesaian dari persamaan tersebut ialah {-2, 2, 3}.
3. Hitunglah himpunan penyelesaian dari persamaan x³ – 3x² – 5x + 15 = 0?
Jawab.
x³ – 3x² – 5x + 15 = 0
x²(x – 3) – 5(x – 3) = 0
(x² – 5)(x – 3) = 0
Jadi himpunan penyelesaian dari persamaan berikut ialah {√5, -√5, 3}.
Baca juga : Contoh Soal Persamaan Irasional Beserta Pembahasannya
Contoh soal persamaan kubik di atas dapat diselesaikan dengan metode pemfaktoran karena bentuk persamaannya cukup sederhana.
Cara Menyelesaikan Persamaan Kubik
Penyelesaian materi persamaan kubik ini pertama kali ditemukan pada tahun 1500an oleh Gerolamo Cardano dan Niccolo Tartaglia selaku ahli Matematikawan dari Italia. Rumus persamaan kubik terkenal sudah ada bahkan sejak jaman romawi dan yunani kuno.
Hingga kini, latihan soal persamaan kubik memang lebih sulit untuk diselesaikan oleh siswa. Tapi dengan pengetahuan, strategi, dan metode yang tepat kita bisa mengerjakan contoh soal persamaan kubik dengan mudahnya.
Jika persamaan kubiknya berbentuk sederhana maka dapat diselesaikan dengan cara di atas. Namun tidak hanya pemfaktoran saja, tetapi adapula cara menyelesaikan persamaan kubik yang berupa metode horner apabila bentuk persamaannya sulit untuk difaktorkan. Semua akarnya masih termasuk bilangan rasional.
Adapula cara menghitung persamaan kubik dengan cara mengubahnya menjadi persamaan kuadrat terlebih dahulu apabila semua akarnya termasuk bilangan irasional.
Penyederhanaan masing masing persamaan kubik yang bentuknya ax³ + bx² + cx + d = 0 dapat berubah menjadi y³ + py + q = 0. Setelah bentuk sederhana ini diperoleh, kemudian nilai y disubstitusikan menggunakan
. Nilai yang disubstitusikan ini dapat digunakan untuk menyederhakan pesamaan kubik menjadi persamaan kuadrat. Adapun langkah langkahnya penyederhanaannya yaitu: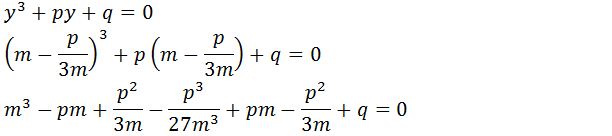
Cara menyelesaikan persamaan kubik selanjutnya yaitu dengan mengalikan m³ dengan kedua ruasnya. Setelah itu akan diperoleh hasil rumus untuk menyelesaikan contoh soal persamaan kubik yang tersedia. Adapun bentuknya yaitu:
Persaaan kuadrat yang dijelaskan dalam m³ memiliki bentuk paling akhir seperti di atas. Persamaan tersebut kemudian dimasukkan dalam rumus ABC sehingga bentuknya dapat menjadi seperti berikut:
Dalam persamaan ini terdapat Diskriminan yang dinyatakan dalam hasil di bawah akar di atas. Adapun rumus diskriminan tersebut yaitu:
Dalam cara menyelesaikan persamaan kubik di atas terdapat peran diskriminan di dalamnya. Untuk itu sebelum membagikan contoh soal persamaan kubik tersebut, anda harus memahami beberapa sifat sifat diskriminan yang dimiliki. Diskriminan ini memiliki beberapa sifat di dalamnya seperti:
- Persamaan kubik mempunyai 2 akar tidak real dan 1 akar real apabila D > 0.
- Persamaan kubik mempunyai akar kembar (baik 3 akar kembar atau 2 akar kembar) apabila D = 0.
- Persamaan kubik mempunyai 3 akar real apabila D < 0.
Demikianlah contoh soal persamaan kubik beserta cara menyelesaikan persamaan kubik yang dapat saya bagikan. Persamaan kubik ialah sebuah persamaan yang mempunyai bentuk umum berupa ax³ + bx² + cx + d = 0, dimana a ≠ 0. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi persamaan kubik di atas.
