Konvers, Invers dan Kontraposisi Dalam Logika Matematika – Dalam pelajaran Matematika terdapat pembelajaran mengenai logika. Materi logika Matematika tersebut memuat beberapa pembahasan di dalamnya seperti konvers invers dan kontraposisi. Materi konvers logika Matematka ini tentunya memiliki rumus yang berbeda dengan materi invers dan materi kontraposisi. Logika tersebut pada dasarnya digunakan ketika manusia sedang berfikir untuk menyelesaikan sebuah masalah tertentu. Namun apakah anda tahu bahwa bekerjanya logika tersebut berlangsung secara matematis? Dalam Matematika tersebut terdapat materi logika yang memuat beberapa rumus di dalamnya.
Dalam materi konvers, invers dan kontraposisi Matematika tersebut memiliki hubungan dengan pernyataan implikasi yang diubah. Implikasi ialah pernyataan majemuk yaang menggunakan kata hubung berupa “jika . . ., maka . . .”. Untuk itu kata hubung jika . . . maka. . . dalam pernyataan majemuk tersebut merupakan ciri khas dari implikasi dalam logika Matematika. Implikasi dalam logika Matematika ini terdapat dalam bentuk anak panah berujung ke kanan berwujud garis lurus. Implikasi tersebut pada dasarnya memiliki simbol berupa “→”. Implikasi juga dapat diartikan sebagai proposisi yang memiliki syarat berupa jika . . . maka . . ..
Nilai kebenaran dalam implikasi dengan suatu pernyataan majemuk dapat berupa Salah/False (S) di sebuah kondisi. Keadaan ini maksudnya yaitu nilai konsekuen salah apabila nilai pernyataan antesedennya benar. Kemudian adapula keadaan lainnya dimana implikasi tersebut memiliki nilai kebenaran berupa Benar/True (B). Nah pada kesempatan kali ini saya akan menjelaskan tentang konvers, invers dan kontraposisi dalam logika Matematika. Untuk lebih jelasnya dapat anda simak di bawah ini.
Konvers, Invers dan Kontraposisi Dalam Logika Matematika
Apabila dalam proposisi tunggal terdapat p dan q. Maka dua proporsi ini memiliki bentuk implikasi jika p maka q. Pada dasarnya syarat perlu dan syarat cukup memang ditercantum dalam suatu implikasi. Apabila dalam implikasi terdapat pernyataan jika p maka q, syarat cukup bagi q ialah p dan syarat perlu bagi p ialah q.
Misalnya jika Ahmad kepanasan maka tubuh Ahmad menjadi berkeringat. Untuk itu tubuh Ahmad menjadi berkeringat disebabkan oleh sakit atau kepanasan karena sinar matahari, api unggun dan sebagainya. Sedangkan syarat perlu bagi Ahmad kepanasan ialah tubuh Ahmad menjadi berkeringat. Inilah salah satu bentuk konsep konvers invers dan kontraposisi.
Baca juga : Perkalian Skalar Dua Vektor Beserta Contoh Soal
Jika p maka q dalam sebuah implikasi tidak ekuivalen atau tidak setara dengan kebalikan jika q maka p dalam implikasi tersebut. Misalnya jika Ahmad kepanasan maka tubuh Ahmad menjadi berkeringat. Berkebalikan dengan jika tubuh Ahmad menjadi berkeringat maka Ahmad kepanasan dalam contoh implikasi tersebut.
Dua pernyataan di atas memiliki keadaan yang berbeda, karena bisa saja tubuh Ahmad menjadi berkeringat disebabkan oleh hal lainnya. Untuk itu dalam sebuah implikasi terdapat kondisi yang berbeda antara konvers invers dan kontraposisi tersebut. Di bawah ini terdapat penjelasan mengenai materi logika Matematika tentang konvers, invers dan kontraposisi. Berikut penjelasan selengkapnya:
Konvers (q → p)
Sebuah implikasi memiliki konvers yang dapat diartikan sebagai sistem yang berubah menjadi sistem lainnya. Konvers dari implikasi ini terdapat dalam pembahasan logika Matematika, dimana keadaannya konsekuen dan anteseden bertukar tempat atau posisi.
Contoh konvers terlihat pada implikasi yang diberikan p → q (jika p maka q). Implikasi tersebut memiliki konvers yang berbentuk q → p (jika q maka p). Kedua implikasi tersebut tidak saling ekuivalen atau berbeda. Di bawah ini terdapat tabel kebenaran konvers dari implikasi yaitu sebagai berikut:
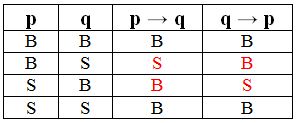
Menurut tabel kebenaran tersebut dapat kita lihat bahwa konvers dan implikasi tersebut memiliki nilai kebenaran yang berbeda. Inilah yang menjadi salah satu hal penting dalam materi konvers, invers dan kontraposisi.
Berdasarkan tabel kebenaran di atas pula dapat kita simpulkan bahwa konvers tidak ekuivalen dengan implikasi. Agar anda lebih paham tentang bentuk konvers dan implikasi tersebut maka saya akan membagikan contoh konvers tersebut. Berikut contoh materi konvers ini yaitu meliputi:
- Implikasi : Jika Ibu memberi uang saku yang banyak maka anak anak menjadi senang.
- Konvers : Jika anak anak menjadi senang maka ibu memberi uang saku yang banyak.
Invers (~p → ~q)
Materi konvers invers dan kontraposisi selanjutnya ialah materi invers dalam logika Matematika. Secara umum invers dapat diartikan sebagai kebalikan aksi dari sebuah fungsi. Invers dari implikasi dalam logika Matematika sama dengan ingkaran konsekuen dan ingkaran anteseden dari bentuk implikasi tersebut.
Jika p maka q (p → q) dalam suatu implikasi maka inversnya dapat berbentuk jika bukan p maka bukan q (~p → ~q). Bentuk dari kedua implikasi tersebut tidak saling ekuivalen atau nilai yang dimiliki berbeda.
Singkatnya, invers melibatkan kondisi dan kesimpulan yang terbalik dari suatu pernyataan. Contoh invers adalah pernyataan awal “Jika hujan, maka atap rumah akan basah”. inversnya adalah “Jika tidak hujan, maka atap rumah pun tidak akan basah”. Pemahaman konsep invers membantu siswa melihat implikasi logis dari suatu pernyataan.
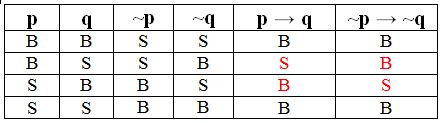
Di bawah ini terdapat tabel kebenaran invers dari implikasi yaitu sebagai berikut:
Baca juga : Contoh Soal Sistem Persamaan Linear 4 Variabel Beserta Cara Menghitung
Menurut tabel kebenaran di atas, nilai kebenaran invers dan implikasi tersebut berbeda. Inilah yang menjadi salah satu hal penting dalam materi konvers, invers dan kontraposisi. Berdasarkan tabel kebenaran tersebut dapat kita simpulkan bahwa invers tidak ekuivalen dengan implikasi. Agar anda lebih paham tentang bentuk invers dan implikasi tersebut, maka saya akan membagikan contoh invers tersebut. Berikut contoh invers ini yaitu meliputi:
- Implikasi : Jika Ibu memberi uang saku yang banyak maka anak anak menjadi senang.
- Invers : Jika Ibu tidak memberi uang saku yang banyak maka anak anak tidak menjadi senang.
Kontraposisi (~q → ~p)
Materi konvers invers dan kontraposisi selanjutnya ialah materi kontraposisi dalam logika Matematika. Pengertian kontraposisi ialah kebalikan dari invers. Kontraposisi memiliki bentuk yang sama dengan ingkaran anteseden dan ingkaran konsekuen dari implikasi.
Sebuah implikasi memiliki bentuk p → q (jika p maka q). Untuk itu implikasi ini memiliki bentuk kontraposisi yang berupa ~q → ~p (jika bukan q maka bukan p). Bentuk kedua implikasi ini ekuivalen. Di bawah ini terdapat tabel kebenaran kontraposisi dari implikasi yaitu sebagai berikut:
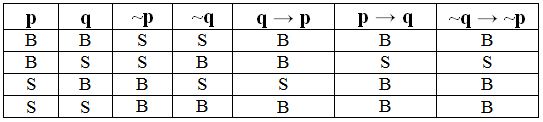
Menurut tabel kebenaran di atas, nilai kebenaran kontraposisi dan implikasi tersebut sama. Inilah yang menjadi salah satu hal penting dalam materi konvers, invers dan kontraposisi. Berdasarkan tabel kebenaran tersebut dapat kita simpulkan bahwa kontraposisi ekuivalen dengan implikasi.
Hubungan Konvers, Invers, Implikasi dan Kontraposisi
Materi konvers invers dan kontraposisi selanjutnya yaitu hubungan antara ketiga materi logika Matematika tersebut. Sebuah implikasi memiliki nilai kebenaran yang ekuivalen dengan kontraposisi. Namun bentuk implikasi ini tidak ekuivalen dengan invers dan konvers. Kemudian dalam implikasi terdapat invers yang nilai kebenarannya ekuivalen dengan konversnya.
Di bawah ini terdapat hubungan antara konvers, invers, implikasi dan kontraposisi yaitu sebagai berikut:
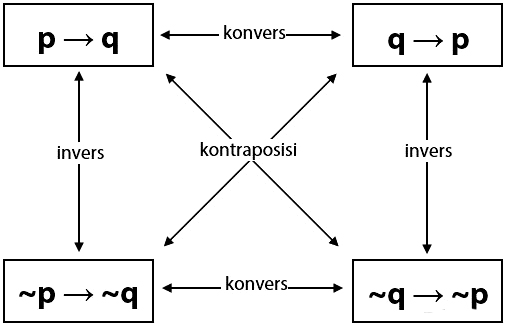
Secara garis besar hubungan konvers, invers, dan kontraposisi memberi dampak besar terhadap pemahaman logika matematika. Sebagai contoh, siswa dapat menggunakan konsep ini untuk membuktikan dari pernyataan dalam matematika terapan.
Demikianlah penjelasan mengenai konvers, invers dan kontraposisi dalam logika Matematika. Dalam materi logika Matematika ini tidak dapat dilepaskan dari adanya bentuk implikasi di dalamnya. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.