Sistem Pertidaksamaan Linear Dua Variabel Beserta Contoh Soal – Dalam pelajaran Matematika terdapat pembahasan mengenai materi pertidaksamaan linear dua variabel. Apakah anda tahu bagaimana cara menyelesaikan contoh soal pertidaksamaan linear dua variabel itu? Dalam sistem pertidaksamaan linear tersebut terdapat dua variabel yang termuat dalam kalimat terbuka Matematika.
Setiap variabel saling terhubung satu sama lain dengan tanda ketidaksamaan dan memiliki derajat satu. Tanda ketidaksamaan yang digunakan dalam sistem pertidaksamaan tersebut dapat berupa <, >, ≤, atau ≥. Tanda tanda inilah yang menjadi simbol pertidaksamaan linear tersebut.

Sistem pertidaksamaan linear dua variabel dapat ditulis dalam bentuk ax + by > c, ax + by < c, ax + by ≥ c, maupun ax + by ≤ c. Berdasarkan bentuk materi pertidaksamaan linear dua variabel tersebut, kita dapat membuat contoh pertidaksamaannya menjadi 3x + 4y > 7, 5x – y < 10 dan sebagainya. Tanda hubung yang digunakan oleh beberapa kalimat terbuka ini dapat berbentuk <, >, ≤, ataupun ≥.
Kalimat terbuka tersebut dapat dinamakan dengan pertidaksamaan karena memiliki tanda tersebut. Cara menyelesaikan contoh soal pertidaksamaan linear dua variabel tentunya berbeda dengan saudaranya (SPLDV) yang berbentuk himpunan pasangan beberapa titik atau bentuknya berupa grafik lurus jika digambarkan.
Sistem Pertidaksamaan Linear Dua Variabel Beserta Contoh Soal
Hampir semua siswa akan kehilangan senyumnya apabila mengerjakan contoh soal sistem pertidaksamaan linear dua variabel. Pendapat itu diperkuat dengan banyak keluhan pada saat guru mulai masuk ke materi. Menghafal rumus hitung, mampu mengerjakan soal dengan benar, dan mampu menyebutkan sifatnya jadi parameter keberhasilan yang harus dicapai.
Saking sulitnya, akhirnya siswa pun mempertanyakan rumus sistem pertidaksamaan linear dua variabel. Karena soal yang berkenaan dengan materi tersebut sangat menguras waktu saat ujian. Banyak dari mereka akhirnya lebih memilih bertanya di internet daripada menghitung sendiri meski tau jawabannya belum tentu benar.
Materi pertidaksamaan linear dua variabel dapat diselesaikan menggunakan daerah penyelesaian yang berbentuk daerah bersih. Lalu bagaimana cara menentukan daerah bersih pada penyelesaian sistem pertidaksamaan linear tersebut?
Pertidaksamaan linear dua variabel merupakan sistem pertidaksamaan yang memiliki dua variabel dan menggunakan tanda ketidaksamaan di dalamnya seperti <, >, ≤, ataupun ≥. Pada kesempatan kali ini saya akan menjelaskan tentang sistem pertidaksamaan linear dua variabel beserta contoh soal pertidaksamaan linear dua variabel. Untuk lebih jelasnya dapat anda simak di bawah ini.
Cara Menyelesaikan Sistem Pertidaksamaan Linear Dua Variabel
Materi pertidaksamaan linear dua variabel dapat diselesaikan menggunakan cara tertentu. Cara menyelesaikan pertidaksamaan linear tersebut tentunya dilakukan dengan beberapa langkah di dalamnya. Adapun langkah langkah penyelesaian pertidaksamaan linear dua variabel yaitu sebagai berikut:
- Langkah pertama yaitu tanda ketidaksamaannya diubah menjadi tanda sama dengan (=) agar persamaan linear dua variabelnya dapat diperoleh.
- Setelah itu gunakan persamaan tersebut untuk menggambar garis atau grafiknya. Cara menggambarnya mudah yaitu dengan menentukan titik potong sumbu x dan y nya dalam persamaan tersebut.
- Kita juga menggunakan titik sembarang yang melalui garisnya sehingga terbentuk dua buah bidang kartesius di dalamnya.
- Setelah itu titik yang tidak dilalui garis tersebut diuji dengan cara mensubstitusikan nilai titik x dan y nya menuju sistem pertidaksamaannya. Jika pernyataan yang dihasilkan benar, maka penyelesaiannya berbentuk daerah tersebut. Namun apabila pernyataan yang dihasilkan salah, maka penyelesaiannya berbentuk bagian lainnya.
Dalam sistem pertidaksamaan linear dua variabel pada dasarnya memiliki bentuk peubah bebasnya yang berupa pangkat satu (linear). Sebelum mempelajari lebih lanjut mengenai materi sistem pertidaksamaan linear ini. Saya akan membagikan beberapa jenis kalimat Matematika seperti berikut:
- Pertidaksamaan linear dengan satu peubah seperti 3x ≥ 6.
- Pertidaksamaan linear dengan dua peubah seperti 2x +y < 0.
- Pertidaksamaan linear dengan dua peubah seperti x – 3y ≤ 4.
- Pertidaksamaan linear dengan tiga peubah seperti x + y – 3z < 0.
Pertidaksamaan linear dua peubah yang satu dengan lainnya dapat digabungkan menjadi suatu sistem pertidaksamaan linear dua peubah. Di bawah ini terdapat contoh sistem pertidaksamaan linear yang memiliki dua peubah diantaranya:
2x + 6y ≤ 24
x + y ≤ 6
x ≥ 0
y ≥ 0
Daerah Himpunan Penyelesaian Pertidaksamaan Linear Dua Variabel
Sistem pertidaksamaan linear dua variabel pada dasarnya dapat diselesaikan menggunakan konsep pasangan berurutan (x, y), dimana pertidaksamaan linear itu dapat dipenuhi nilainya. Untuk menyatakan himpunan penyelesaian pertidaksamaan linear dua peubah dapat dilakukan dalam bentuk daerah yang diarsir pada bidang kartesius.
Baca juga : Contoh Soal Sistem Persamaan Linear 4 Variabel Beserta Cara Menghitung
Agar anda lebih paham mengenai materi tersebut, maka perhatikan contoh soal pertidaksamaan linear dua variabel seperti di bawah ini:
Contoh Soal
Hitunglah himpunan penyelesaian pertidaksamaan linear berikut ini:
a. 6x + 8y ≥ 24
b. 3x – 6y > 18
Jawab.
a. Untuk menyelesaikan sistem pertidaksamaan linear tersebut dapat dilakukan dengan cara mencari titik potong garis pada sumbu Y dan sumbu X terlebih dahulu. Hal ini dilakukan agar garis 6x + 8y ≥ 24 dapat dilukis.
Baca juga : Contoh Soal Bilangan Berpangkat Negatif Beserta Pengertian
Pada sumbu X terdapat titik potong garis dengan y = 0 sehingga diperoleh nilai x = 4, dimana titik potongnya (4,0).
Pada sumbu Y terdapat titik potong garis dengan x = 0 sehingga diperoleh nilai y = 3, dimana titik potongnya (0,3).
Cara menyelesaikan contoh soal sistem pertidaksamaan linear dua variabel selanjutnya yaitu membagi bidang kartesius menjadi dua bagian sesuai dengan garis 6x + 8y = 24 tersebut. Untuk itu salah satu titik uji diambil dari satu sisi daerahnya untuk menentukan daerah himpunan penyelesaiannya. Contohnya saja titik (0, 0) yang diambil. Langkah berikutnya yaitu mensubstitusikan titik tadi pada pertidaksamaan tersebut, maka hasilnya akan menjadi:
6x + 8y ≥ 24
6(0) + 8(0) ≥ 24
0 ≥ 24
Berdasarkan perhitungan di atas ditemukan nilai 0 ≥ 24, dimana pernyataan ini salah sehingga tidak memenuhi ketentuan untuk membuat daerah penyelesaian. Maka dari itu titik (0, 0) tidak termasuk dalam daerah penyelesaian. Adapun gambar daerah yang diarsir dalam pertidaksamaan tersebut yaitu:
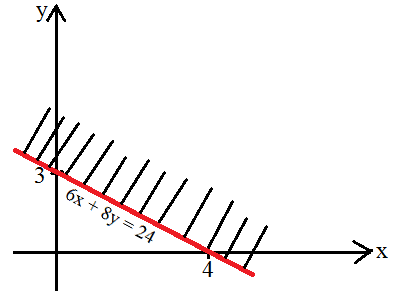
Jawaban dan Pembahasan
b. Untuk menyelesaikan sistem pertidaksamaan linear dua variabel tersebut dapat dilakukan dengan cara mencari titik potong garis pada sumbu Y dan sumbu X terlebih dahulu. Hal ini dilakukan agar garis 3x – 6y > 18 dapat dilukis.
Pada sumbu X terdapat titik potong garis dengan y = 0 sehingga diperoleh nilai x = 6, dimana titik potongnya (6, 0).
Pada sumbu Y terdapat titik potong garis dengan x = 0 sehingga diperoleh nilai y = -3, dimana titik potongnya (0, -3).
Cara menyelesaikan contoh soal pertidaksamaan linear dua variabel selanjutnya yaitu membagi bidang kartesius menjadi dua bagian sesuai dengan garis 3x – 6y = 18 tersebut. Untuk itu salah satu titik uji diambil dari satu sisi daerahnya untuk menentukan daerah himpunan penyelesaiannya. Contohnya saja titik (0, 0) yang diambil. Langkah berikutnya yaitu mensubstitusikan titik tadi pada pertidaksamaan tersebut, maka hasilnya akan menjadi:
3x – 6y > 18
3(0) – 6(0) > 18
0 > 18
Berdasarkan perhitungan di atas ditemukan nilai 0 > 18, dimana pernyataan ini salah sehingga tidak memenuhi ketentuan untuk membuat daerah penyelesaian sistem pertidaksamaan linear dua variabel. Maka dari itu titik (0, 0) tidak termasuk dalam daerah penyelesaian. Adapun gambar daerah yang diarsir dalam pertidaksamaan tersebut yaitu:
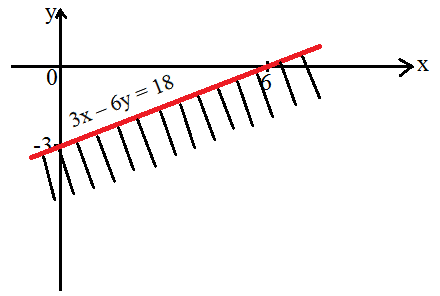
Demikianlah penjelasan mengenai sistem pertidaksamaan linear dua variabel beserta contoh soal pertidaksamaan linear dua variabel. Pertidaksamaan linear dua variabel ialah sistem pertidaksamaan yang memiliki dua variabel dan menggunakan tanda ketidaksamaan di dalamnya seperti <, >, ≤, ataupun ≥. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.


