Materi Irisan Dua Lingkaran Beserta Contoh Soal Lengkap – Ketika di bangku sekolah kelas 11 tentunya para siswa telah diajarkan mengenai irisan dua lingkaran. Apa pengertian irisan dua lingkaran itu? Apa saja jenis jenis irisan dua lingkaran? Bagaimana cara menyelesaikan contoh soal irisan dua lingkaran? Irisan dua lingkaran dapat dinamakan dengan irisan dua bundar. Bentuknya yang bundar ini membuat maknanya disamakan dengan lingkaran. Maka dari itulah irisan tersebut juga disebut juga dengan irisan bundar. Materi Matematika ini memiliki beberapa pembahasan lain di dalamnya. Pembahasan pembahasan tersebut tentunya berkaitan dengan hal hal yang bernuansa lingkaran, sesuai dengan namanya yaitu irisan dua lingkaran.
Sebelum mempelajari tentang materi irisan dua lingkaran dan contoh soal irisan dua lingkaran, anda harus memahami terlebih dahulu mengenai lingkaran. Pengertian lingkaran ialah himpunan beberapa titik dengan titik tertentu, dimana jarak yang dimiliki sama. Titik tertentu ini disebut juga dengan pusat lingkaran. Titik titik inilah nantinya yang akan berkaitan dengan dua buah lingkaran saling beririsan. Kita dapat mengamati dua buah lingkaran yang saling beririsan dalam penjelasan yang akan saya berikan. Misalnya terdapat lingkaran yang memiliki pusatnya masing masing di A dan B. Dimana setiap lingkaran memiliki jari jari r2 dan r1. Maka akan terjadi irisan dua lingkaran jika AB < r1 + r2.
Dalam materi irisan lingkaran pada dasarnya terdapat beberapa materi lainnya yang akan di bahas seperti kedudukan dua lingkaran, luas dan keliling irisan dua lingkaran, berkas lingkaran, garis singgung persekutuan lingkaran serta kuasa pada lingkaran. Materi materi lingkaran ini memiliki penjelasan yang berbeda beda, karena rumus yang digunakannyapun juga tidak sama. Nah pada kesempatan kali ini saya akan menjelaskan tentang materi irisan dua lingkaran beserta contoh soal irisan dua lingkaran lengkap. Untuk lebih jelasnya dapat anda simak di bawah ini.
Materi Irisan Dua Lingkaran Beserta Contoh Soal Lengkap
Materi irisan lingkaran tentunya berbeda dengan materi irisan kerucut. Hal ini dikarenakan irisan kerucut sendiri dapat dibagi menjadi beberapa jenis yaitu berbentuk lingkaran, parabola, elips dan hiperbola. Sedangkan dalam irisan dua lingkaran hanya terdapat berbagai hal yang berhubungan dengan lingkaran saja. Seperti yang telah kita ketahui bahwa lingkaran merupakan beberapa titik yang terhimpun dengan titik tertentu, dimana jarak yang dimiliki panjangnya sama.
Baca juga : Contoh Soal Peluang Beserta Pembahasan Terlengkap
Dalam materi irisan lingkaran terdapat beberapa hal yang dibahas seperti kedudukan dua lingkaran, luas dan keliling irisan dua lingkaran, berkas lingkaran, garis singgung persekutuan lingkaran serta kuasa pada lingkaran. Jika dua sentra bundar memiliki jarak berupa M1M3 serta jari jari kedua lingkaran berupa r1 dan r2, maka irisan dua lingkarannya akan seperti di bawah ini:
Berpotongan
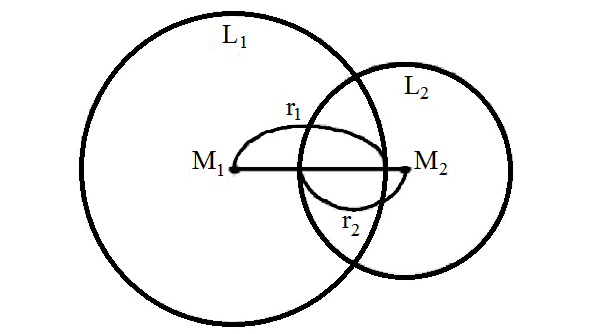
Jenis irisan dua lingkaran yang pertama dapat saling berptongaan. Dua lingkaran dapat dikatakan saling berpotongan apabila kedua titik sentra lingkaran memiliki jarak berupa M1M2 < r1 + r2. Berikut gambar dua lingkaran saling berpotongan yaitu:
Bersinggungan
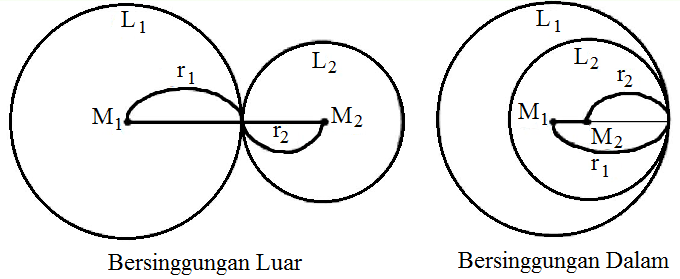
Materi irisan dua lingkaran selanjutnya ialah materi lingkaran bersinggungan. Dua lingkaran dapat dikatakan saling bersinggungan luar apabila kedua titik sentra bundar memiliki jarak yang berupa M1M2 = r1 + r2. Sedangkan dua lingkaran dapat dikatakan saling bersinggungan dalam apabila kedua titik sentra lingkaran memiliki jarak yang berupa M1M2 = |r1 – r1|. Adapun gambar dua lingkaran saling bersinggungan yaitu sebagai berikut:
Tidak Bersinggungan
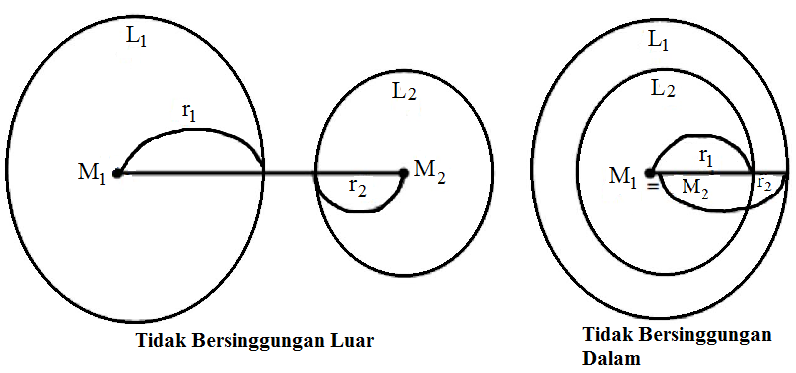
Materi irisan lingkaran selanjutnya membahas tentang dua lingkaran tidak bersinggungan. Dua lingkaran dikatakan saling tidak bersinggungan luar apabila kedua titik sentra lingkarannya memiliki jarak berupa M1M2 > r1 + r2. Sedangkan dua lingkaran dikatakan saling tidak bersinggungan dalam apabila kedua titik sentra lingkarannya memiliki jarak r2 > r1 dan berjumlah nol, karena M1 = M2 sehingga M1M2 = 0. Kemudian dua lingkaran yang dinyatakan tidak bersinggungan dalam jika letak salah satu lingkarannya berada di dalam lingkaran lainnya sehingga r2 > r1 dan M1 ≠ M2.
Baca juga : Cara Menghitung Luas Bangun Datar Segi Banyak Beserta Contoh Soal
Dalam materi irisan lingkaran ini juga terdapat pembahasan mengenai garis singgung komplotan dalam dan luar. Panjang garis singgung komplotan dalam ialah terbentuknya panjang ruas garis yang berasal dari garis singgung komplotan dalam dengan titik titik singgung lingkarannya. Maka dari itu bentuk gambarnya akan menjadi seperti di bawah ini:
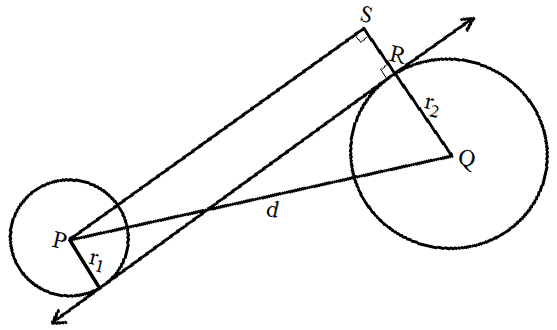
Dalam materi irisan dua lingkaran ini kita tahu bahwa jari jari yang dimiliki oleh panjang garis singgung komplotan luar dapat berupa r1 dan r2, dimana r1 > r2. Untuk itu kedua sentra lingkaran d memiliki jarak seperti persamaan berikut:![]()
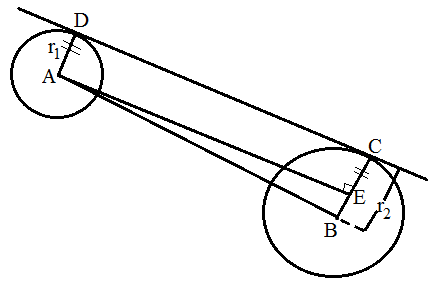
Dalam materi irisan lingkaran ini kita tahu bahwa jari jari yang dimiliki oleh panjang garis singgung komplotan dalam dapat berupa r1 dan r2. Untuk itu kedua sentra lingkaran d memiliki jarak seperti persamaan berikut:![]()
Contoh Soal Irisan Dua Lingkaran
Setelah memahas tentang materi irisan dua lingkaran di atas. Selanjutnya saya akan membagikan contoh soal irisan lingkaran terkait materi di atas. Adapun contoh soal dan pembahasannya yaitu sebagai berikut:
Baca juga : Materi Bilangan Bulat (Pengertian, Operasi Hitung dan Contoh)
Diketahui persamaan lingkaran L1 : x² + y² + 6x + 4y – 51 = 0 dan L2 : x² + y² – 6x – 4y – 23 = 0. Tunjukkan apabila kedua lingkaran ini saling berpotongan?
Pembahasan.
Contoh soal irisan dua lingkaran ini dapat diselesaikan dengan langkah langkah berikut:
Dua lingkaran dikatakan saling berpotongan apabila memenuhi syarat berupa kedua titik pusat lingkaran memiliki jarak yang lebih kecil dibandingkan jumlah jari jari kedua lingkarannya. Untuk itu M1M2 < r1 + r2, dimana M1M2 = jarak dua pusat lingkaran dan r1, r2 = jari jari pada kedua lingkaran. Dalam materi irisan dua lingkaran tersebut, kita harus menentukan nilai M1, M2, r1 dan r2 terlebih dahulu. Maka:
L1 : x² + y² + 6x + 4y – 51 = 0
Pusat M1 (-1/2 A , -1/2 B) = (-1/2 (6) , -1/2 (4)) = (-3, -2)![]()
L2 : x² + y² – 6x – 4y – 23 = 0
Pusat M2 (-1/2 A , -1/2 B) = (-1/2 (-6) , -1/2 (-4)) = (3, 2)![]()
Apabila jarak (-3, -2) menuju (3, 2) ialah M1M2. Maka:
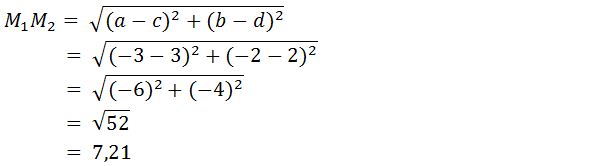
Nilai M1M2 = 7,21 dan r1 + r2 = 8 + 6 = 14, sehingga nilai M1M2 < r1 + r2
Jadi terbukti bahwa kedua lingkaran saling berpotongan.
Demikianlan penjelasan mengenai materi irisan dua lingkaran beserta contoh soal irisan dua lingkaran lengkap. Lingkaran merupakan himpunan beberapa titik dengan titik tertentu dengan jarak yang sama. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.


