Pengertian Bilangan Imajiner Beserta Contohnya – Apakah anda tahu definisi bilangan imajiner itu? Bagaimana contoh bilangan imajiner? Sebenarnya bilangan imajiner ini diberikan nama yang merupakan bilangan dalam imajinasi dan tidak nyata dalam pemecahan masalah di Matematika. Untuk itulah penamaan ini masih menjadi kontroversi. Bahkan penamaan bilangan imajiner ini memperoleh penolakan dari Gauss. Namun bilangan imajiner ini lebih suka disebut oleh Gauss sebagai bilangan lateral. Arti bilangan lateral ialah letak biangan yang tegak lurus ada di dimensi lain dengan bilangan natural.
Penyebutan bilangan imajiner dan riil telah disepakati oleh para Matematikawan sehingga tidak disebut sebagai bilangan lateral dan natural. Apa pengertian bilangan imajiner itu? Apa saja contoh bilangan imajiner? Sekarang ini kita dapat mengetahui bilagan dua dimensi (imajiner dan riil) sebagai bilagan kompleks sehingga tidak hanya satu dimensi saja (bilangan riil). Luasnya perspektif yang dimiliki tersebut dapat menyebabkan penyelesaian masalah menjadi lebih mudah, baik dalam Fisika, Teknik maupun Matematika.
Pengertian Bilangan Imajiner Beserta Contohnya
Tidak semua orang mampu menjabarkan definisi bilangan imajiner dengan baik dann benar. Dalam ilmu matematika banyak yang mengaitkannya dengan bilangan riil. Maka dari itu, sebelum mengerjakan soal kita wajib mengetahui terlebih dulu apa itu bilangan riil. Pada kesempatan kali ini saya akan menjelaskan tentang pengertian bilangan imajiner beserta contoh bilangan imajiner. Untuk lebih jelasnya dapat anda simak di bawah ini.
Bilangan imajiner dapat dinamakan dengan bilangan khayal karena sifat yang dimiliki oleh bilangan ini yaitu i² = -1. Bilangan imajiner pada umumnya termasuk dalam bilangan kompleks, tetapi bilangan imajiner juga termasuk dalam bilangan riil. Bilangan imajiner berdasarkan definisinya dapat digunakan untuk menyelesaikan persamaan kuadratik x² + 1 = 0 yang ekuivalen sehingga dapat menjadi x = √-1 atau x² = -1. Maka dari itu bilangan imajiner memuat hal hal dalam Matematika yang berbentuk akar negatif.
Baca juga : Rumus Penjumlahan Bilangan Berpangkat Beserta Contoh Soal
Pengertian bilangan imajiner dalam bidang Matematika aljabar ialah bilangan yang maknanya sama dengan i² = -1, dimana angka imajiner ini dilambangkan dengan huruf i. Dalam bahasa Inggris, bilangan i dapat dinamakan dengan imaginary number. Penggunaan nilai imajiner ini biasanya dalam ilmu Fisika dan teknik elektro.
Persamaan Kuadratik Bilangan Imajiner
Setelah menjelaskan tentang definisi bilangan imajiner, selanjutnya saya akan membahas tentang persamaan kuadratik bilangan imajiner. Persamaan kuadratik yang diperoleh dari nilai bilangan imajiner dapat berbentuk seperti di bawah ini:
- x² + 1 = 0
- x² = -1
- x = √-1
Nilai x tersebut tidak dimiliki secara numerik, hal ini dikarenakan hanya nilai √-1 yang memenuhinya. Untuk itu simbol i berguna untuk menjelaskan nilai tersebut. Dari sini kita dapat memperoleh x = √-1 = i, maka:
i² = i × i
= √-1 × √-1
= -1
Jadi diperoleh nilai imajiner dalam bentuk i² = -1.
Baca juga : Materi Irisan Dua Lingkaran Beserta Contoh Soal Lengkap
Berdasarkan pengertian bilangan imajiner di atas, kita dapat menghasilkan pola teratur dalam perpangkatan angka imajiner dan bilangan bulat dalam bentuk di bawah ini: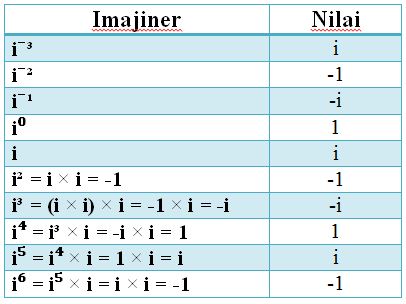
Contoh Bilangan Imajiner
Selain definisi bilangan imajiner di atas, adapula contoh bilangan imajiner. Bilangan imajiner memang termasuk dalam kategori bilangan kompleks. Bilangan kompleks sendiri dapat diartikan sebagai sistem bilangan berbentuk a + bi dalam ilmu Matematika, dimana i ialah angka imajiner dan a,b ialah bilangan real. Adapun beberapa contoh pada bilangan imajiner yaitu meliputi:
- i
- -i
- 6i
- -4i
- 3i
- 3 + 2i
- 7 – 6i
- 5 + 6i
- -7 + 6i
- i³
Demikianlah penjelasan mengenai pengertian bilangan imajiner beserta contoh bilangan imajiner. Bilangan imajiner merupakan bilangan yang maknanya sama dengan i² = -1, dimana angka imajiner ini dilambangkan dengan huruf i. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.