Rumus Turunan Fungsi Logaritma Beserta Contoh Soal – Hampir semua siswa sekolah menengah familiar ketika ditanya apa itu log x. Logx sendiri mengacu pada rumus logaritma yang notabenya dianggap sulit. Di lain sisi kita pun tak bisa menampik fakta bahwa materi log memang menyulitkan karena cara menghitungnya cukup kompleks. Padahal materi satu ini sudah pasti muncul sebagai butir soal ketika ujian baik itu PAT, PAS, maupun sekedar ulangan harian.
Apakah anda tahu bagaimana cara menyelesaikan contoh soal turunan fungsi logaritma matematika? Turunan dapat diartikan sebagai suatu perhitungan nilai fungsi yang mengalami perubahan akibat nilai input yang juga berubah (variabel). Turunan tersebut dapat dinamakan dengan diferensial. Sedangkan penentuan turunan sebuah fungsi dapat dinamakan dengan diferensiasi. Turunan tersebut dapat diterapkan dalam beberapa hal seperti untuk menghitung gradien pada garis singgung kurva, mencari interval pada fungsi turun atau naik dan sebagainya.
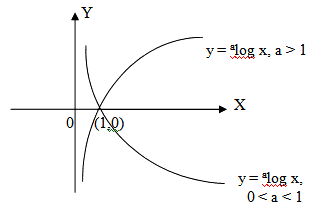
Penerapan turunan pada umumnya juga ditemukan dalam nilai stasioner sebuah fungsi, permasalahan yang berhubungan dengan persamaan gerak, maupun permasalahan yang berhubungan dengan maksimum minimum. Kemudian adapula definisi logaritma yang merupakan sebuah kebalikan atau operasi invers dari perpangkatan. Logaritma dapat ditulis dalam bentuk ᵃlog b = c, dimana a = basis logaritma, b = numerus (bilangan yang akan ditentukan nilai logaritma) dan c = nilai atau besar pangkat logaritma. Apakah anda tahu bagaimana rumus turunan fungsi logaritma? Bagaimana contoh soal turunan fungsi logaritma?
Rumus Turunan Fungsi Logaritma Beserta Contoh Soal
Materi yang sedikit banyak membahas logaritma sebenarnya sudah mulai diberikan pada siswa ketika duduk di bangku sekolah menengah. Meski tak memiliki cakupan luas tapi rumus hitung yang kompleks membuat banyak orang kewalahan menyelesaikan soalnya. Hal ini pun dibuktikan dengan banyaknya frekuensi pertanyaan bagaimana cara menghitung log x, turunan fungsi in, dan lain sebagainya. Padahal guru pasti sudah memberikan pembekalan serta pendalaman materi. Di lain sisi, latihan soal turunan fungsi logaritma juga dapat kita jumpai di buku LKS.
Materi turunan fungsi pada logaritma sebenarnya telah dipelajari ketika dibangku sekolah. Materi ini merupakan salah satu pembahasan turunan fungsi selain aljabar maupun trigonometri. Untuk itu sebelum mempelajari lebih lanjut mengenai turunan fungsi pada logaritma, alangkah lebih baik jika anda memahami konsep logaritma terlebih dahulu. Pada kesempatan kali ini saya akan menjelaskan tentang rumus turunan fungsi logaritma beserta contoh soal turunan fungsi logaritma. Untuk lebih jelasnya dapat anda simak di bawah ini.
Bentuk Turunan Fungsi Logaritma
Dalam materi turunan fungsi sebuah logaritma pada dasarnya menggunakan konsep logaritma secara umum. Bentuk sederhana fungsi logaritma tersebut dapat berupa y = ᵃlog x, dimana a = basis dan x = numerusnya. Di bawah ini terdapat bentuk turunan fungsi logaritma yang paling sederhana yaitu sebagai berikut:
y = ᵃlog x → y’ = 1/x . ᵃlog e
y = ᵃlog g(x) → y’ = g'(x)/g(x) . ᵃlog e
Keterangan:
e =Bilangan euler yang nilainya 2,7182818…
Agar anda lebih paham mengenai rumus turunan fungsi logaritma yang sederhana di atas. Maka saya akan membagikan contoh soal terkait rumus tersebut. Adapun contoh soal dan pembahasannya yaitu:
Baca juga : Contoh Soal Persamaan Garis Singgung Dengan Turunan Lengkap
Tentukan nilai turunan fungsi logaritma seperti di bawah ini:
1. y = ²log x
2. y = ²log(3x³ – x² + x – 8)
Pembahasan.
Contoh soal turunan fungsi logaritma tersebut dapat diselesaikan dengan langkah langkah seperti berikut:
1. y = ²log x → y’ = 1/x . ²log e
2. Untuk contoh ini kita buat permisalan g(x) = 3x³ – x² + x – 8 sehingga g'(x) = 9x² – 2x + 1. Maka hasilnya akan menjadi seperti di bawah ini:
y = ²log x (3x³ – x² + x – 8)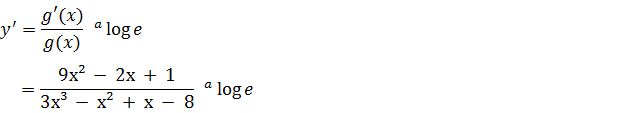
Jadi nilai turunan pertamanya ialah
.
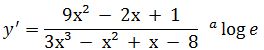Turunan Fungsi ln
Rumus turunan fungsi logaritma di atas tidak hanya menggunakan konsep dasar saja. Namun turunan ini juga menggunakan konsep turunan fungsi ln yang dibaca len. Sebenarnya bentuk ln ini serupa dengan logaritma (log), tetapi di dalamnya terdapat e yang menjadi basisnya. Sifat sifat ln ini juga hampir sama dengan sifat pada logaritma, sehingga bentuknya dapat menjadi seperti berikut:
ᵉlog x = ᵉln x = ln x
ᵉlog g(x) = ᵉln g(x) = ln g(x)
Dari penjelasan di atas dapat ditemukan rumus turunan fungsi ln seperti berikut:
y = ln x → y’ = 1/x
y = ln g(x) → y’ = g'(x)/g(x)
Rumus di atas memang secara konsep hampir sama dengan rumus turunan fungsi logaritma secara sederhana. Di bawah ini terdapat pembuktian turunan ln dengan sifat logaritma ᵃlog a = 1 dan dengan turunan logaritma yaitu sebagai berikut:
Baca juga : Rumus Perkalian Bilangan Berpangkat Pecahan Beserta Contoh Soal
Rumus y = ln x → y’ = 1/x
y = ᵃlog x → y’ = 1/x . ᵃlog e
y = ln x = ᵉlog x → y’ = 1/x . ᵉlog e = 1/x . 1 = 1/x
Sehingga dapat diperoleh y = ln x → y’ = 1/x
Rumus y = ln g(x) → y’ = g'(x)/g(x)
y = ᵃlog g(x) → y’ = g'(x)/g(x) . ᵃlog e
y = ln g(x) = ᵉlog g(x) → y’ = g'(x)/g(x) . ᵉlog e = g'(x)/g(x) . 1 = g'(x)/g(x)
Sehingga dapat diperoleh y = ln g(x) → y’ = g'(x)/g(x)
Dari penjelasan di atas kita tahu bahwa rumus turunan fungsi logaritma sederhana tersebut dapat digunakan untuk membuktikan rumus dari turunan fungsi ln. Agar anda lebih paham mengenai rumus turunan fungsi ln di atas. Maka saya akan membagikan contoh soal turunan fungsi ln seperti pada contoh soal turunan fungsi logaritma sebelumnya. Berikut contoh soal dan pembahasannya:
Tentukan nilai turunan fungsi ln seperti di bawah ini:
1. y = ln x
2. y = ln (x² – 4x + 2)
Pembahasan.
1. y = ln x → y’ = 1/x
2. Kita buat permisalan g(x) = x² – 4x + 2 sehingga g'(x) = 2x – 4. Maka:
y = ln (x² – 4x + 2)
y’ = g'(x)/g(x) = (2x – 4) / (x² – 4x + 2)
Sekian penjelasan mengenai rumus turunan fungsi logaritma beserta contoh soal turunan fungsi logaritma . Turunan fungsi pada logaritma menggunakan konsep turunan pada umumnya yang berbentuk ᵃlog b = c. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.
