Cara Menyusun Persamaan Kuadrat Cepat dan Contoh Soal – Persamaan kuadrat secara umum dapat dinyatakan dalam bentuk ax² + bx + c = 0. Dalam materi persamaan kuadrat baru ini sering muncul pertanyaan bagaimana cara menentukan persamaan kuadrat apabila nilai koefisien a, b atau c telah diketahui. Apakah anda tahu bagaimana cara penyusunan persamaan kuadrat baru itu? Bagaimana cara menyelesaikan contoh soal menyusun persamaan kuadrat baru itu?
Akar akar persamaan kuadrat baru sendiri dapat ditentukan dengan memanfaatkan koefisien a, b, dan c yang telah diketahui tadi, begitupula sebaliknya. Kita dapat menggunakan persamaan kuadrat apabila belum mengetahui nilai koefisien a, b ataupun c nya. Selain itu persamaan kuadrat baru tersebut dapat disusun menggunakan akar akar kuadrat yang telah diketahui.
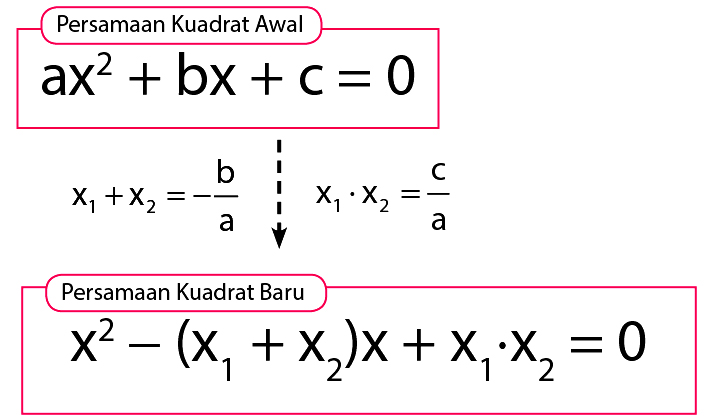
Bagaimana cara menyusun persamaan kuadrat baru itu? Bagaimana cara menyelesaikan contoh soal menyusun persamaan kuadrat baru itu? Persamaan kuadrat baru dapat ditentukan dengan mudah menggunakan akar akar persamaan baru yang dikaitkan dengan akar akar persamaan kuadrat yang telah diketahui. Penyusunan persamaan kuadrat yang baru dapat dilakukan menggunakan beberapa metode. Metode metode tersebut memiliki cara pengerjaan yang berbeda beda. Namun sebelum itu anda harus mengetahui terlebih dahulu mengenai pengertian persamaan kuadrat.
Cara Menyusun Persamaan Kuadrat Cepat dan Contoh Soal
Dalam penyusunan persamaan kuadrat baru sebenarnya memiliki hubungan antara persamaan yang lama dengan persamaan baru. Dalam persamaan baru biasanya memiliki bentuk ax² + bx + c dengan akar akar yang berupa x₁ dan x₂. Sedangkan persamaan kuadrat baru memiliki bentuk px² + bx + c dengan akar akar yang berupa y₁ dan y₂. Persamaan kuadrat baru ini dibentuk dari persamaan kuadrat lama yang dapat dinyatakan dalam bentuk ax² + bx + c tadi. Lalu bagaimana cara menyusun persamaan kuadrat baru itu? Pada kesempatan kali ini saya akan menjelaskan tentang tentang persamaan kuadrat baru dan contoh soal menyusun persamaan kuadrat baru.
Seperti yang telah kita ketahui bahwa akar akar persamaan kuadrat lama dengan akar akar persamaan kuadrat baru masih memiliki hubungan. Persamaan kuadrat baru dapat disusun menggunakan prinsip dasar yang berupa rumus jumlah dan hasil kali. Kedua rumus ini dapat digunakan untuk menyusun persamaan kuadrat baru yang berhubungan dengan akar akar terkait.
Baca juga : Latihan Soal Matriks SMA Ujian dan Ulangan Harian Beserta Pembahasannya
Cara menyusun persamaan kuadrat baru yang mengandung akar akar x₁ dan x₂ tersebut dapat dilakukan dengan dua cara. Cara yang pertama yaitu menggunakan faktor. Sedangkan cara kedua menggunakan rumus jumlah dan hasil kali akar. Berikut penjelasan mengenai cara menyusun dan contoh soal menyusun persamaan kuadrat baru yaitu diantaranya:
Menggunakan Faktor
Cara penyusunan persamaan kuadrat baru yang pertama yaitu menggunakan faktor. Dalam faktor tersebut biasanya menggunakan bentuk seperti di bawah ini:
(x – x₁)(x – x₂) = 0
Agar anda lebih paham mengenai cara ini, maka saya akan membagikan contoh soal terkait cara tersebut. Berikut contoh soal dan pembahasannya:
1. Hitunglah persamaan kuadrat yang memiliki akar akar berupa 2 dan 4?
Pembahasan.
Contoh soal menyusun persamaan kuadrat baru ini dapat diselesaikan dengan cara berikut:
x1 = 2
x2 = 4
Maka,
(x – x1)(x – x2) = 0
(x – 2)(x – 4) = 0
x² – 6x + 8 = 0
Jadi persamaan kuadratnya ialah x² – 6x + 8 = 0.
2. Hitunglah persamaan kuadrat yang memiliki akar akar berupa 6 dan -3?
Pembahasan.
Cara menyusun persamaan kuadrat baru ini dapat diselesaikan dengan cara berikut:
x1 = 6
x2 = -3
Maka,
(x – x1)(x – x2) = 0
(x – 6)(x + 3) = 0
x² – 3x – 18 = 0
Jadi persamaan kuadratnya ialah x² – 3x – 18 = 0.
Baca juga : Rumus Pemuaian Zat Gas Beserta Contoh Soalnya
Menggunakan Rumus Jumlah dan Hasil Kali Akar
Cara penyusunan persamaan kuadrat baru selanjutnya yaitu menggunakan rumus jumlah dan hasil kali akar. Dalam rumus tersebut biasanya menggunakan bentuk seperti di bawah ini:
x² – (x₁ + x₂)x +x₁ .x₂
Agar anda lebih paham mengenai cara ini, maka saya akan membagikan contoh soal menyusun persamaan kuadrat baru tersebut. Berikut contoh soal dan pembahasannya:
1. Diketahui persamaan kuadrat x² + 6x + 5 = 0 memiliki akar akar x1 dan x2. Hitunglah persamaan kuadrat baru yang akar akarnya berupa 3×1 dan 3×2?
Pembahasan.
Cara menyusun persamaan kuadrat baru tersebut dapat diselesaikan dengan metode berikut:
x² + 6x + 5 = 0, dimana a = 1, b = 6 dan c = 5
x1 + x2 = -b/a = -6
x1.x2 = c/a = 5
Sehingga,
Persamaan kuadrat barunya yaitu:
x² – (3×1 + 3×2)x + (3×1.3×2) = 0
x² – 3(x1 + x2)x + 9(x1.x2) = 0
x² – 3(-6)x + 9(5) = 0
x² + 18x + 45 = 0
Jadi persamaan kuadrat barunya ialah x² + 18x + 45 = 0.
2. Hitunglah persamaan kuadrat baru dari x² + 6x – 4 = 0 dengan akar akar yang berkebalikan?
Pembahasan.
Contoh soal menyusun persamaan kuadrat baru ini dapat diselesaikan dengan cara berikut:
x² + 6x – 4 = 0, dimana a = 1, b = 6 dan c = -4
x1 + x2= -b/a = -6
x1.x2 = c/a = -4
Cara menyusun persamaan kuadrat baru tersebut memiliki akar akar berupa:
α = 1/x1
β = 1/x2
Sehingga,
x² – (1/x1 + 1/x2)x + 1/x1x2 = 0
x² – ((x1 + x2)/x1x2) + 1/x1x2 = 0
x² – ((-6)/(-4))x + 1/(-4) = 0
x² – (3/2)x – 1/4 = 0
4x² – 6x – 1 = 0
Jadi persamaan kuadrat barunya ialah 4x² – 6x – 1 = 0.
Sekian penjelasan mengenai cara menyusun persamaan kuadrat baru dan contoh soal menyusun persamaan kuadrat baru. Penyusunan persamaan kuadrat baru tersebut dapat diselesaikan dengan menggunakan faktor maupun menggunakan rumus jumlah dan hasil kali akar. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.