Apa Itu Relasi dan Fungsi Dalam Matematika Terlengkap – Apa pengertian relasi itu? Apa pengertian fungsi? Materi relasi dan fungsi pada dasarnya juga dipelajari dalam ilmu Matematika. Dalam relasi Matematika tersebut tentunya memuat himpunan. Relasi merupakan sebuah aturan yang digunakan pada anggota himpunan untuk dihubungkan ke anggota himpunan lainnya. Misalnya himpunan A yang dihubungkan dengan himpunan B sehingga anggota anggota di dalamnya dapat saling terkait. Relasi dan fungsi tentunya adalah dua hal yang saling berbeda. Namun keduanya juga memiliki persamaan tertentu.
Apa itu relasi? Apa itu fungsi? Pengertian relasi secara sederhana ialah sebuah hubungan. Hubungan yang dimaksud ialah hubungan antara domain (daerah asal) dengan kodomain (daerah kawan). Kemudian adapula fungsi yang merupakan relasi setiap anggota himpunan daerah asal yang dipasangkan dengan himpunan daerah kawan secara tepat satu per satu. Apakah anda tahu perbedaan relasi dan fungsi itu? Relasi dan fungsi memiliki perbedaan yang letaknya ada dicara memasangkan anggota pada himpunan kawan menuju daerah asalnya.
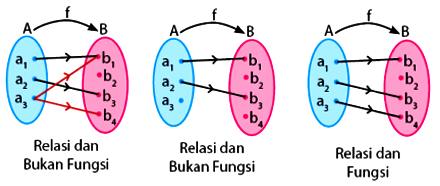
Pada umumnya setiap anggota himpunan daerah asal dapat dipasangkan dengan anggota himpunan daerah kawan tanpa membutuhkan aturan khusus. Keterikatan aturan tersebut hanya terdapat dalam pernyataan relasi itu sendiri. Masing masing anggota pada himpunan daerah asal diperbolehkan untuk tidak mempunyai pasangan atau memiliki pasangan berjumlah satu maupun lebih. Lantas apa pengertian relasi dalam Matematika itu? Apa pengertian fungsi dalam Matematika? Pada kesempatan kali ini saya akan menjelaskan tentang apa itu relasi dalam matematika dan apa itu fungsi dalam matematika terlengkap. Untuk lebih jelasnya dapat anda simak di bawah ini.
Apa Itu Relasi dan Fungsi Dalam Matematika Terlengkap
Relasi dan fungsi matematika adalah dua konsep yang berbeda meskipun saling memiliki keterikatan serta hubungan antara dua atau lebih nilai objek. Banyak yang mempertanyakan perbedaan tersebut dari segi rumus dan cara mengerjakan.
Relasi sama sekali tidak terikat oleh aturan spesifik sehingga siswa lebih mudah mengerjakan soal relasi. Lain halnya dengan fungsi yang notabenya memiliki aturan khusus untuk memasng setiap anggota himpunan daerah asal. Dengan aturan khusus ini diharapkan setiap anggota himpunan daerah asal dalam fungsi dapat dipasangkan dengan daerah kawannya secara tepat hanya satu anggota.
Baca juga : 1 Ton Berapa Kg? Konversi dan Contoh Soal
Dari penjelasan ini dapat kita simpulkan bahwa masing masing relasi tidak dapat dikategorikan sebagai fungsi. Tetapi masing masing fungsi tentunya adalah relasi. Apa itu relasi? Apa itu fungsi? Di bawah ini terdapat penjelasan mengenai pengertian relasi dalam Matematika dan pengertian fungsi dalam Matematika. Berikut penjelasan selengkapnya:
Daerah Asal, Daerah Kawan dan Hasil
Dalam sebuah himpunan tentunya terdapat jenis jenis daerah yang terdapat dalam pembahasan materi relasi dan fungsi. Macam macam daerah yang dimaksud ialah domain (daerah asal), kodomain (daerah kawan) dan range (daerah hasil). Himpunan ketiga daerah tersebut secara umum dapat dinyatakan dalam bentuk seperti berikut ini:
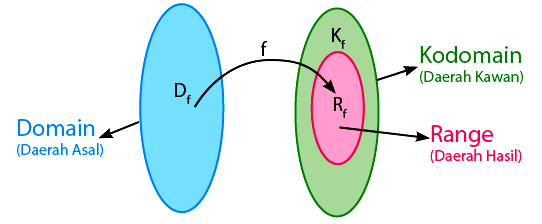
Sebelum membahas tentang apa itu relasi Matematika dan apa itu fungsi dalam Matematika. Maka alangkah lebih baik jika anda memahami pengertian domain, pengertian kodomain dan pengertian range terlebih dahulu. Berikut penjelasannya yaitu:
- Daerah asal (domain) ialah himpunan tidak kosong sehingga memiliki anggota yang didefinisikan sebagai suatu relasi.
- Daerah kawan (kodomain) ialah himpunan tidak kosong yang memiliki anggota domain yang didefinisikan sebagai sebuah pasangan sesuai dengan relasinya.
- Daerah hasil (range) ialah seluruh anggota daerah kawan yang mempunyai pasangan dalam anggota daerah asal.
Relasi
Pengertian relasi secara sederhana memang merupakan suatu hubungan. Contohnya hubungan perkalian yang dinyatakan dalam bentuk relasi. Relasi ini memiliki hasil yang ditunjukkan dalam bentuk himpunan pasangan x dan y secara berurutan dalam bidang kartesius.
Himpunan A yang dikalikan dengan himpunan B akan menghasilkan relasi tertentu. Untuk lebih jelasnya dapat anda perhatikan contoh di berikut ini:
A = {1, 3, 4}
B = {3, 4}
A x B = {3, 9, 12, 4, 12, 16}
Baca juga : 1 Kg Berapa Liter? Beserta Konversi dan Contoh Soalnya
Memahami apa itu relasi dan apa itu fungsi memang sangat penting untuk mengetahui maksud dari contoh relasi yang akan saya bagikan ini. Jika sebuah fungsi f(x) sudah dimetakan dalam suatu relasi, dimana A dikalikan dengan B. Maka himpunan x akan memiliki anggota yang berupa semua anggota A. Sedangkan himpunan y atau f(x) memiliki anggota yang berupa hasil perkalian antara anggota A dengan B. Untuk itu hasil relasinya akan seperti di bawah ini:
x = {1, 3, 4}
y = {3, 9, 12, 4, 12, 16}
Hasil contoh relasi ini dapat dinyatakan dalam bidang kartesius seperti di bawah ini:

Fungsi (Pemetaan)
Setelah menjelaskan pengertian relasi, selanjutnya saya akan membahas tentang pengertian fungsi atau pemetaan. Fungsi atau pemetaan pada umumnya tergolong dalam kategori relasi. Sebuah fungsi dapat dinamakan fungsi apabila himpunan daerah asalnya memiliki semua anggota yang dipasangkan dengan daerah kawan tepat satu per satu. Himpunan A ke B yang dimetakan oleh sebuah fungsi dapat disimbolkan dalam bentuk f : A → B.
Agar anda lebih paham mengenai apa itu relasi dan apa itu fungsi tersebut. Maka perhatikan contoh fungsi dalam masalah himpunan A dan B seperti berikut ini:
A = {1, 2, 3, 4, 5}
B = {1, 2, 3, 4, …, 10}
Jika fungsi f : A → B dimana f(x) = x + 4. Maka tentukan hasil pemetaan x ∈ A pada fungsi f, Df, Kf dan Rf?
Pembahasan.
Fungsi f pada peta x ∈ A dapat berupa y = f(x) = x + 4. Maka,
f(1) = 1 + 4 = 5
f(2) = 2 + 4 = 6
f(3) = 3 + 4 = 7
f(4) = 4 + 4 = 8
f(5) = 5 + 4 = 9
Daerah hasil (range) pada pengerjaan di atas dapat dilihat pada perhitungan f(x) nya. Kemudian untuk domain (daerah asal) dapat berupa seluruh anggota pada himpunan A. Sedangkan kodomain (daerah kawan) dapat berupa seluruh anggota pada himpunan B. Untuk itu hasilnya akan menjadi seperti berikut ini:
- Domain (daerah asal) : Df = A = {1, 2, 3, 4, 5}
- Kodomain (daerah kawan) : Kf = B = {1, 2, 3, 4, …, 10}
- Range (daerah hasil) : Rf = {5, 6, 7, 8, 9}
Sifat Sifat Fungsi
Setelah menjelaskan apa itu relasi, pengertian relasi, apa itu fungsi dan pengertian fungsi tersebut. Selanjutnya saya akan membahas tentang sifat sifat pada fungsi Matematika. Fungsi berdasarkan sifatnya dapat dikategorikan menjadi beberapa jenis seperti fungsi surjektif, fungsi bijektif dan fungsi injektif. Adapun penjelasannya yaitu sebagai berikut:
Fungsi Injektif / Fungsi Into / Fungsi Satu Satu
Fungsi injektif dapat menyatakan fungsi f : A → B jika dan hanya jika kodomainnya memiliki anggota yang dipasangkan dengan anggota domain sebanyak satu kali saja. Anggota himpunan kodomain pada fungsi injektif diperbolehkan untuk tidak mempunyai pasangan. Akan tetapi kodomainnya memiliki semua anggota yang terpasang sebanyak satu kali saja sehingga anggotanya tidak lebih dari satu. Untuk lebih jelasnya perhatikan contoh fungsi injektif seperti berikut ini:
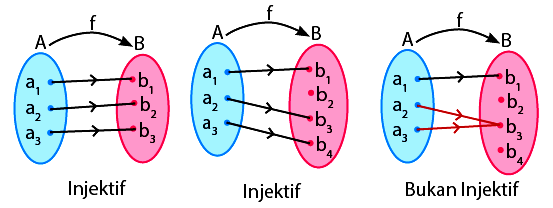
Fungsi Surjektif (Fungsi Onto)
Selain penjelasan mengenai apa itu relasi dan apa itu fungsi. Adapula pembahasan mengenai sifat fungsi surjektif. Ciri ciri fungsi surjektif atau fungsi onto ialah kodomainnya memiliki anggota yang pasangannya dapat lebih dari satu. Akan tetapi anggota kodomainnya tidak diperbolehkan untuk tidak memiliki pasangan. Biasanya fungsi surjektif dipenuhi jika kodomainnya memiliki jumlah anggota yang lebih sedikit atau sama dengan anggota domainnya. Untuk lebih jelasnya perhatikan contoh fungsi surjektif seperti di bawah ini:
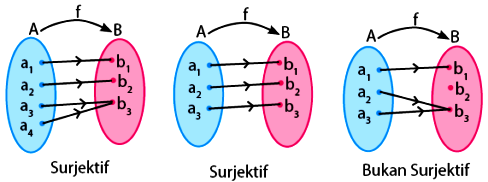
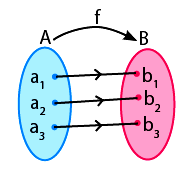
Fungsi Bijektif (Korespondensi Satu Satu)
Pengertian fungsi bijektif ialah fungsi injektif yang digabungkan dengan fungsi surjektif. Semua anggota domain pada fungsi bijekfif terpasangkan tepat satu dengan anggota kodomainnya. Fungsi injektif dan fungsi surjektif memiliki kebalikan yang berupa belum pasti pemetaan/fungsinya. Sedangkan fungsi bijektif memiliki kebalikan yang berupa pemetaan/fungsi itu sendiri. Untuk lebih jelasnya perhatikan contoh fungsi bijektif seperti di bawah ini:
Demikianlah penjelasan mengenai apa itu relasi dalam matematika dan apa itu fungsi dalam matematika terlengkap. Materi relasi dan fungsi dalam Matematika pada dasarnya memiliki persamaan dan perbedaannya sendiri. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.


