Pengertian Turunan, Rumus, Jenis Jenis dan Contoh Soal Terlengkap – Apa itu turunan? Bagaimana rumus turunan itu? Apa saja jenis jenis turunan? Bagaimana cara menyelesaikan contoh soal turunan? Kita tahu bahwa materi turunan ini termasuk dalam pembelajaran Matematika. Ilmu Matematika sendiri sering dianggap beberapa orang sebagai ilmu yang menyenangkan karena cakupannya cukup luas. Untuk itu apabila di rincikan lebih detail lagi, maka hasil pengukuran dan pembahasan Matematika ini sangat luas. Akan tetapi tidak jarang pula orang menganggap ilmu Matematika sebagai ilmu yang sulit untuk dipahami karena menggunakan berbagai rumus di dalamnya.
Dalam ilmu Matematika memang diajarkan mengenai materi turunan. Dalam materi tersebut terdapat pembahasan mengenai pengertian turunan, rumus turunan, jenis jenis turunan, penerapan turunan dan contoh soal turunan. Turunan merupakan pengukuran perubahan fungsi disebabkan oleh nilai input yang berubah. Turunan tersebut digunakan untuk menjelaskan sebuah perubahan besaran karena besaran lainnya berubah. Penemuan turunan tersebut dilakukan dengan menggunakan proses bernama diferensiasi.
Materi turunan memang harus dipahami dan dipelajari. Untuk mempelajari materi tersebut biasanya menggunakan konsep limit. Dengan begitu pemahaman dan pembelajaran materi turunan Matematika dapat dilakukan dengan mudah. Turunan memang merupakan materi lanjutan dari pembelajaran limit fungsi. Pada kesempatan kali ini saya akan menjelaskan tentang pengertian turunan, rumus turunan, jenis jenis turunan, penerapan turunan dan contoh soal turunan. Untuk lebih jelasnya dapat anda simak di bawah ini.
Pengertian Turunan, Rumus, Jenis Jenis dan Contoh Soal Terlengkap
Turunan dapat diartikan sebagai sebuah perhitungan pada nilai fungsi yang berubah karena variabel (nilai input) mengalami perubahan. Turunan secara umum dapat dinamakan dengan diferensial. Sedangkan turunan fungsi tersebut dapat ditentukan dengan proses bernama diferensiasi. Turunan berdasarkan konsep limit tersebut dapat dinyatakan dalam persamaan di bawah ini:
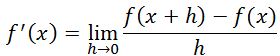
Baca juga : Konversi Satuan Volume Dalam Kubik dan Liter
Pengertian turunan memang merupakan sebuah limit karena rata ratanya berubah dari nilai fungsi bervariabel x. Sebelum menjelaskan tentang rumus turunan, jenis jenis turunan dan contoh soal turunan. Maka saya akan membagikan beberapa penerapan turunan terlebih dahulu yaitu diantaranya:
- Turunan diterapkan pada perhitungan gradien garis singgung sebuah kurva.
- Turunan diterapkan pada penentuan interval sebuah fungsi, baik fungsi turun atau fungsi naik.
- Turunan diterapkan pada penentuan nilai stasioner sebuah fungsi.
- Turunan diterapkan pada penyelesaian masalah yang berhubungan dengan persamaan gerak.
- Turunan berguna untuk menyelesaikan masalah minimum maksimum.
Rumus Turunan
Menghafal rumus hitung adalah kunci utama apabila kita ingin mengerjakan contoh soal turunan matematika dengan benar. Selain itu, siswa juga dituntut harus teliti pada saat menghitung. Karena banyak yang gagal lantaran salah pada saat memasukan bilangan ke dalam rumus.
Rumus turunan matematika sendiri dapat kita jumpai pada buku pedoman pembelajaran. Selain dari buku, guru biasanya juga akan mengajarkan cara mengerjakan soal turunan secara intensif. Tujuannya tak lain sebagai pembelakan terhadap siswa agar mereka mampu mengerjakan ujian di kemudian hari.
Turunan memiliki rumus dasar yang dapat dinyatakan dalam bentuk persamaan seperti di bawah ini:
- f(x) = c dengan turunan f'(x) = 0, dimana c = Konstanta.
- f(x) = x dengan turunan f'(x) = 1.
- f(x) = axⁿ dengan turunan f'(x) = anxⁿ‾¹.
- Penjumlahan fungsi yang berbentuk h(x) = f(x) + g(x) dengan turunan h'(x) = f'(x) + g'(x).
- Pengurangan fungsi berbentuk h(x) = f(x) – g(x) dengan turunan h'(x) = f'(x) – g'(x).
- Perkalian konstanta fungsi berbentuk (kf)(x) dengan turunan k. f'(x)
Jenis Jenis Turunan Matematika
Ada banyak sekali jenis turunan matematika yang harus di hafalkan oleh siswa. Masing-masing memiliki peranan serta manfaat yang berbeda. Dengan kata lain rumus turunan itu sendiri pun juga akan memiliki perbedaan yang signifikan.
Setelah menjelaskan tentang pengertian turunan dan fungsi turunan di atas. Selanjutnya saya akan membahas tentang macam macam fungsi. Fungsi secara umum dapat dibagi menjadi beberapa jenis yaitu diantaranya:
Turunan Fungsi
Sebuah fungsi dimisalkan memiliki bentuk f(x) = axⁿ. Maka fungsi tersebut memiliki turunan berupa f'(x) = anxⁿ‾¹. Untuk lebih jelasnya dapat anda perhatikan contoh soal turunan fungsi di bawah ini:
Tentukan turunan dari:
1. f(x) = 4x³
2. g(x) = -6y‾³
Pembahasan.
1. f'(x) = 4(3)x³‾¹ = 12x²
2. g'(x) = -6(-3)x‾³‾¹ = 18x‾⁴
Baca juga : Rumus Konversi Satuan Panjang dan Cara Menghitungnya
Turunan Fungsi Aljabar
Selain pengertian turunan di atas, adapula jenis jenis turunan yang berupa turunan fungsi aljabar. Dalam materi turunan tersebut berisi penjelasan mengenai bentuk perkalian turunan yang terdapat di pembagian fungsi aljabar. Bentuk perkalian turunan fungsi aljabar ini dapat dimisalkan dalam bentuk seperti berikut:
h(x) = u(x) . v(x)
Dengan turunan fungsi h'(x) = u'(x) . v(x) + u(x) . v'(x)
Keterangan:
h(x) = Fungsi berbentuk perkalian
h'(x) = Turunan fungsi berbentuk perkalian
u(x), v(x) = Fungsi bervariabel x
u'(x), v'(x) = Turunan fungsi bervariabel x
Selain rumus turunan fungsi aljabar berbentuk perkalian di atas. Adapula rumus pembagian turunan fungsi aljabar yang dimisalkan dalam bentuk seperti di bawah ini:
h(x) = u(x)/v(x)
Dengan Turunan fungsi h'(x) = (u'(x) . v(x) – u(x) . v'(x))/v²(x)
Keterangan:
h(x) = Fungsi berbentuk pembagian
h'(x) = Turunan fungsi berbentuk pembagian
u(x), v(x) = Fungsi bervariabel x
u'(x), v'(x) = Turunan fungsi bervariabel x
Turunan Akar
Selain pengertian turunan di atas, adapula jenis jenis turunan yang berupa turunan akar. Fungsi akar ini dapat dimisalkan dalam bentuk seperti berikut:
![]()
Turunan fungsi tersebut dapat ditentukan dengan cara diubah menjadi bentuk fungsi perpangkatan terlebih dahulu. Fungsi perpangkatan tersebut memiliki bentuk berupa![]() . Fungsi ini memiliki turunan yang bentuknya
. Fungsi ini memiliki turunan yang bentuknya![]() .
.
Pada dasarnya rumus turunan akar ini tidak hanya itu saja. Hal ini dikarenanan fungsi akar sendiri dapat berbentuk seperti berikut:
![]()
Turunan fungsi di atas dapat ditentukan menggunakan cara yang hampir sama seperti di atas yaitu mengubahnya menjadi bentuk perpangkatan terlebih dahulu. Untuk itu bentuknya akan menjadi seperti![]() dengan turunan
dengan turunan![]() .
.
Turunan Parsial
Jenis jenis turunan selanjutnya ialah turunan parsial. Pengertian turunan parsial ialah sebuah turunan yang memiliki banyak fungsi peubah tertentu dan mempertahankan peubah lainnya. Kita dapat membuat permisalan sebuah fungsi yang berbentuk f(x, y) = 3xy. Fungsi parsial ini memiliki turunan dengan variabel x yang bentuknya fₓ'(x, y) = 3y.
Kita juga dapat memahami materi ini pada contoh soal turunan lainnya yang berbentuk g(x, y) = -4xy². Fungsi parsial ini memiliki turunan dengan variabel y yang bentuknya fy(x, y) = -8xy.
Baca juga : 1 Ton Berapa Kg? Konversi dan Contoh Soal
Turunan Implisit
Macam macam turunan selanjutnya ialah turunan implisit. Berdasarkan variabel dalam fungsinya terdapat rumus turunan implisit seperti di bawah ini:
- Sebuah fungsi yang variabelnya x, maka turunannya berbentuk x d/dx.
- Sebuah fungsi yang variabelnya y, maka turunannya berbentuk y d/dy. dy/dx.
- Sebuah fungsi yang variabelnya x maupun y, maka turunannya berbentuk xy d/dx + xy d/dy . dy/dx.
Contoh Soal Turunan
Kita bisa menjumpai contoh soal turunan dengan mudah pada buku latihan siswa. Hadirnya internet pun seolah juga memudahkan siswa mencari berbagai variasi latihan soal turunan dengan tingkat kesulitan berbeda. Di lain sisi, melatih diri adalah langkah yang tepat setelah kita mempelajari setiap aspek di atas.
Setelah menjelaskan tentang pengertian turunan, rumus turunan, jenis jenis turunan dan penerapan turunan di atas. Selanjutnya saya akan membagikan contoh soal materi turunan terkait rumus tersebut. Berikut contoh soal dan pembahasannya yaitu:
Tentukan turunan fungsi di bawah ini:
1. f(x) = 9
2. g(x) = 4x + 6
3. h(x) = 7x³
4. k(x) = (4x² + 5)⁴
Pembahasan.
1. f'(x) = 0
2. g'(x) = 4
3. h'(x) = 7(3)x³‾¹ = 21x²
4. k'(x)= 4(4x² + 5)⁴‾¹ . 8x = 32x . (4x² + 5)³
Demikianlah penjelasan mengenai pengertian turunan, rumus turunan, jenis jenis turunan, penerapan turunan dan contoh soal turunan. Turunan merupakan sebuah perhitungan pada nilai fungsi yang berubah karena variabel (nilai input) mengalami perubahan. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi turunan di atas.