Rumus Luas Permukaan Irisan Tabung Beserta Contoh Soal – Tabung adalah bangun ruang tiga dimensi yang dapat kita jumpai hampir setiap harinya. Misalnya pada toren air, botol air mineral, gelas minuman, dan lain sebagainya yang mengambil bentuk dasar lingkaran. Sebagai bangun ruang tentunya kita bisa menghitung volume serta luas permukaan tabung menggunakan rumus hitung tertentu.
Dalam dunia pendidikan kita pasti sudah sangat familiar ketika diminta kedua rumus di atas. Tapi bagaimana jika kalian menjumpai contoh soal irisan tabung? tak semua siswa hafal materi tersebut. Mayoritas justru salah saat menyebutkan rumus irisan tabung dengan benar. Hal ini disebabkan karena siswa tak tau seperti apa bentuk irisan tabung.
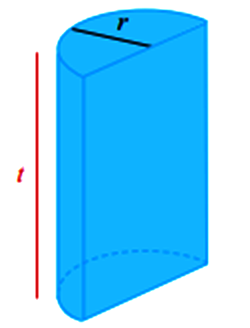
Lantas bagaimana cara menghitung luas permukaan irisan tabung? Bagaimana contoh soal luas permukaan irisan tabung? Pada umumnya rumus luas irisan tabung berasal dari rumus luas permukaan tabung yang dibagi dua. Hal ini dikarenakan irisan tabung tersebut asalnya dari pembagian bangun tabung yang diubah menjadi dua bagian dengan pembatas berupa bangun persegi panjang. Maka dari itu dalam rumus ini nantinya akan ada peran rumus persegi panjang di dalamnya.
Rumus Luas Permukaan Irisan Tabung Beserta Contoh Soal
Menghitung soal irisan tabung bukanlah pekerjaan yang mudah. Hal ini dibuktikan dengan banyaknya siswa yang gagal menjawab pertanyaan ketika ujian maupun ulangan harian. Meski guru sudah menjelaskan materi secara detail tapi faktanya masih ada siswa yang merasa kesulitan menghafal rumus irisan tabung.
Ketika di bangku sekolah tentunya kita pernah diajarkan mengenai materi irisan tabung. Dalam materi ini terdapat pembahasan mengenai rumus luas permukaan irisan tabung dan contoh soal luas permukaan irisan tabung. Tabung sendiri secara umum terdiri dari dua bangun lingkaran yang dikelilingi oleh selimut tabung berbentuk persegi panjang. Untuk itu apabila bangun ini diperinci menjadi jaring jaring tabung, maka akan terlihat dua buah lingkaran dan satu persegi panjang yang menyusunnya.
Apakah anda tahu bagaimana rumus luas permukaan tabung secara umum? Rumus ini berperan penting untuk memperoleh rumus luas irisan tabung tersebut. Dengan begitu soal soal yang tersedia dapat diselesaikan dengan mudah menggunakan rumus irisan tabung ini. Pada kesempatan kali ini saya akan menjelaskan tentang rumus luas permukaan irisan tabung dan contoh soal luas permukaan irisan tabung.
Rumus Luas Permukaan Irisan Tabung
Ingin menyelesaikan contoh soal luas permukaan irisan tabung? Langkah pertama yang harus kalian lakukan adalah mencari luas kedua lingkaran serta selimutnya terlebih dahulu. Jika dibelah maka bangun ruang satu ini akan menyerupai bentuk bangun datar yakni persegi panjang. kalian bisa melakukan praktek dengan memotong karton persegi panjang lalu menggulungnya hingga mendapat bentuk tabung.
Dimana panjang (p) persegi panjang dapat dinyatakan dalam bentuk keliling lingkaran (2πr). Sedangkan lebar (l) persegi panjang dapat dinyatakan dalam bentuk tinggi tabung (t). Dengan demikian, rumus luas selimut tabung dapat dijabarkan dalam bentuk persamaan seperti di bawah ini:
Luas Selimut = p . l
Luas Selimut = 2πr . t
Luas Selimut = 2πrtBaca juga : Contoh Soal Sistem Persamaan Kuadrat Kuadrat (SPKK) dan Jawaban
Luas permukaan tabung berasal dari penjumlahan luas selimut tabung, luas tutup dan luas alasnya. Luas inilah yang digunakan untuk memperoleh rumus luas permukaan irisan tabung. Lalu bagaimana bentuk luas permukaan tabung secara umum? Tabung memiliki rumus luas permukaan yang bentuknya:
Luas Tabung = Luas Alas + Luas Tutup + Luas Selimut
Luas Tabung = 2(Luas Alas) + Luas Selimut
Luas Tabung = 2πr2 + 2πrt
Luas Tabung = 2πr(r + t)
Seperti yang telah kita ketahui bahwa rumus luas permukaan tabung dapat dinyatakan dalam bentuk 2πr(r + t). Kemudian kita juga dapat menentukan rumus luas irisan tabung berdasarkan rumus luas tadi. Dalam rumus irisan tabung ini terdapat pembagian luas tabung yang ditambah dengan luas persegi panjang. Jika dinyatakan dalam bentuk persamaan, maka hasilnya akan seperti di bawah ini:
Luas permukaan irisan = [(2 . π . r² + 2 . π . r . t)/2] + 2r . t
Luas permukaan irisan = π . r² + π . r . t + 2r . t
Luas permukaan irisan = r . (π.r + π.t + 2t)
Baca juga : Rumus Kesebangunan Segitiga Beserta Contoh Soal
Dari persamaan di atas dapat kita temukan rumus luas permukaan irisan tabung yaitu:
Luas permukaan irisan = r . (π.r + π.t + 2t)
Contoh Soal Irisan Tabung
Secara garis besar latihan soal luas permukaan irisan tabung bisa kita temukan di buku LKS. Internet pun juga menjadi sumber tak terbatas untuk menambah referensi ataupun sekedar mengasah pengetahuan. Kalian bisa mencari berbagai model soal irisan tabung sesuai tingkatan mulai yang mudah sampai kompleks.
Saya akan asumsikan kalian sudah memahami rumus luas irisan tabung di atas. Selanjutnya kita akan masuk ke sesi mengerjakan latihan soal irisan tabung terkait rumus tersebut. Berikut contoh soal dan pembahasannya yaitu:
Diketahui jari jari irisan tabung 10 cm dengan tinggi 8 cm. Tentukan luas permukaannya?
Pembahasan.
r = 10 cm
t = 8 cm
Luas permukaan irisan = r . (π.r + π.t + 2t)
= 10 . (3,14 . 10 + 3,14 . 8 + 2 . 8)
= 10 . (31,4 + 25,12 + 16)
= 10 . 72,52
= 725,2 cm²
Jadi luas permukaan irisan tabung tersebut ialah 725,2 cm².
Demikianlah penjelasan mengenai rumus luas permukaan irisan tabung dan contoh soal luas permukaan irisan tabung. Rumus luas irisan tabung pada umumnya berasal dari luas tabung yang dibagi dua dan ditambah dengan luas persegi panjang. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi luas irisan tabung di atas.


