Sifat Sifat Persamaan Eksponen dan Pertidaksamaan Eksponen – Matematika menjadi salah satu pelajaran yang cukup ditakuti siswa. Cakupan materi begitu luas serta rumus hitung yang kompleks menjadi alasan utamana. Dari sekian banyaknya materi kalian akan menjumpai pembahasan eksponen ketika berada di bangku sekolah menengah.
Bagaimana cara menyelesaikan persamaan eksponen? Apa saja sifat fungsi persamaan eksponen? Apa saja sifat sifat pertidaksamaan eksponen? Bagaimana cara menyelesaikan pertidaksamaan eksponen? Pada umumnya contoh soal persamaan eksponen dan contoh soal pertidaksamaan eksponen dapat diselesaikan dengan cara yang berbeda. Apa yang dimaksud eksponen? Pengertian eksponen ialah operasi hitung Matematika yang berhubungan dengan bilangan berpangkat.
Bilangan berpangkat tersebut dapat dihitung dengan cara bilangan sejenis dikalikan sejumlah bilangan pangkat di dalamnya. Contohnya 3² = 3 x 3 = 9. Persamaan eksponen dan pertidaksamaan eksponen menjelaskan tentang operasi hitung yang berkaitan dengan bentuk pangkat. Dalam pembahasan tersebut, ada beberapa hal yang perlu di pahami yaitu sifat sifat persamaan eksponen, sifat sifat pertidaksamaan eksponen, cara menyelesaikan persamaan eksponen, cara menyelesaikan pertidaksamaan eksponen, contoh soal persamaan eksponen dan contoh soal pertidaksamaan eksponen.
Sifat Sifat Persamaan Eksponen dan Pertidaksamaan Eksponen
Persamaan eksponen dan pertidaksamaan eksponen memiliki perbedaan yaitu memiliki tanda hubung yang mengaitkan ruas ruasnya. Kita dapat menghubungkan persamaan eksponen menggunakan tanda sama dengan (=). Kemudian kita dapat menghubungkan pertidaksamaan eksponen dengan tanda pertidaksamaan seperti >, <, ≥ dan ≤. Bagaimana cara menyelesaikan persamaan eksponen? Apa rumus pertidaksamaan eksponen?
Persamaan dan pertidaksamaan eksponen secara umum memiliki bentuk soal yang berupa bilangan berpangkat dengan variabel di dalamnya. Biasanya para siswa diharuskan untuk mencari nilai variabel yang memenuhi persamaan atau pertidaksamaan tersebut. Maka dari itu penting sekali memahami cara menyelesaikan persamaan eksponen dan cara menyelesaikan pertidaksamaan eksponen.
Baca juga : Rumus Pertidaksamaan Logaritma dan Contoh Soalnya
Materi persamaan dan pertidaksamaan eksponen ini sering kali ditemukan dalam soal soal ujian Matematika, baik ujian sekolah maupun ujian Nasional. Di bawah ini terdapat penjelasan mengenai apa saja sifat persamaan eksponen, sifat sifat pertidaksamaan eksponen, contoh soal persamaan eksponen dan contoh soal pertidaksamaan eksponen yaitu sebagai berikut
Persamaan Eksponen
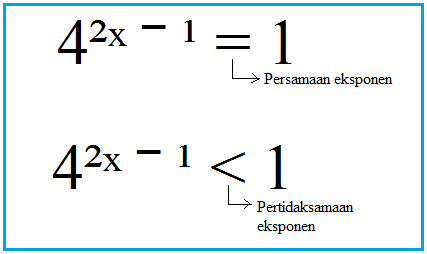
Dua buah fungsi pada bilangan berpangkat yang memiliki tanda sama dengan sebagai penghubungnya dapat dikatakan sebagai persamaan eksponen. Contoh yaitu suatu bilangan berpangkat fungsi linier yakni 4²ˣ ‾ ¹ = 1. Nilai x yang memenuhi persamaan tersebut ialah x = ½ sehingga menghasilkn persamaan 4⁰ = 1.
Bagaimana cara menyelesaikan persamaan eksponen ini. Di bawah ini terdapat pembahasan mengenai sifat sifat persamaan eksponen yaitu meliputi:
- a⁰= 1
- a‾¹ = 1/a
- aᵐ × aⁿ = aᵐ ⁺ ⁿ
- aᵐ : aⁿ = aᵐ ‾ ⁿ
- (aᵐ)ⁿ = aᵐ ˣ ⁿ
- (aᵐ × aⁿ)ᵖ = aᵖᵐ ⁺ᵖⁿ
Kemudian persamaan eksponen juga memilki beberapa sifat fungsi yang ada didalamnya. Berikut sifat sifat fungsi eksponen yaitu diantaranya:
- Apabila aᶠ⁽ˣ⁾ = aᴾ, maka f(x) = P
- Apabila aᶠ⁽ˣ⁾ = aᶢ⁽ˣ⁾, maka f(x) = g(x)
Sifat sifat fungsi eksponen dan sifat sifat persamaan eksponen di atas dapat anda gunakan untuk menyelesaikan contoh soal persamaan eksponen yang ada. Perhatikan contoh persamaan eksponen sebelumnya yaitu 4²ˣ ‾ ¹ = 1. Berikut penjabaran cara menyelesaikan persamaan eksponen untuk memperoleh nilai x = ½ yaitu:
4²ˣ ‾ ¹ = 1
4²ˣ ‾ ¹ = 3⁰
2x – 1 = 0
2x = 1
x = ½
Baca juga : Materi Pengukuran Waktu (Alat Ukur dan Contoh Soalnya)
Pertidaksamaan Eksponen
Selanjutnya saya akan menjelaskan tentang sifat sifat pertidaksamaan eksponen. Pada dasarnya cara menyelesaikan pertidaksamaan eksponen tidak jauh berbeda dengan persamaan eksponen. Pertidaksamaan eksponen memiliki karakteristik yaitu menggunakan tanda pertidaksamaan untuk menghubugkan dua fungsi bilangan berpangkat. Tanda pertidaksamaan yang dimaksud dapat berbentuk < (kurang dari), > (lebih dari), ≤ (kurang dari/sama dengan) dan ≥ (lebih dari/sama dengan).
Pertidaksamaan eksponen ini memiliki beberapa sifat yang digunakan untuk menyelesaikan soal soal yang ada. Adapun beberapa sifat tersebut yaitu:
Untuk a ≥ 1 yaitu:
- aᶠ⁽ˣ⁾ < aᶢ⁽ˣ⁾ → f(x) < g(x)
- aᶠ⁽ˣ⁾ > aᶢ⁽ˣ⁾ → f(x) > g(x)
- aᶠ⁽ˣ⁾ ≤ aᶢ⁽ˣ⁾ → f(x) ≤ g(x)
- aᶠ⁽ˣ⁾ ≥ aᶢ⁽ˣ⁾ → f(x) ≥ g(x)
Untuk a < a < 1 yaitu:
- aᶠ⁽ˣ⁾ < aᶢ⁽ˣ⁾ → f(x) > g(x)
- aᶠ⁽ˣ⁾ > aᶢ⁽ˣ⁾ → f(x) < g(x)
- aᶠ⁽ˣ⁾ ≤ aᶢ⁽ˣ⁾ → f(x) ≥ g(x)
- aᶠ⁽ˣ⁾ ≥ aᶢ⁽ˣ⁾ → f(x) ≤ g(x)
Agar anda lebih paham mengenai sifat sifat pertidaksamaan eksponen tersebut. Berikut contoh soal pertidaksamaan eksponen beserta pembahasannya yaitu:
Tentukan nilai x yang memenuhi pertidaksamaan 4²ˣ ‾ ¹ < 1?
Pembahasan.
4²ˣ ‾ ¹ < 1
4²ˣ ‾ ¹ < 4⁰
2x – 1 < 0
2x < 1
x < ½
Jadi pertidaksamaan 4²ˣ ‾ ¹ < 1 memiliki nilai x yang memenuhinya yaitu x < ½.
Persamaan eksponen dan pertidaksamaan eksponen memiliki perbedaan yang terletak pada hasil akhirnya. Hasil akhir penyelesaian persamaan eksponen dapat berbentuk sebuah bilangan. Sedangkan pertidaksamaan eksponen memiliki hasil akhir penyelesaian berbentuk daerah yang memenuhi pertidaksamaan tersebut. Sekian penjelasan mengenai sifat sifat persamaan eksponen dan sifat sifat pertidaksamaan eksponen. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.