Rumus Perkalian Pangkat dan Contoh Soalnya – Istilah pangkat tentunya sudah tidak asing lagi untuk kita. Perpangkatan tersebut merupakan satu dari sekian materi Matematika yang masuk dalam kisi kisi ujian, baik ujian sekolah ataupun ujian nasional. Bilangan pangkat secara umum memiliki operasi hitungnya sendiri yaitu perkalian, pembagian, dan sebagainya. Materi perpangkatan ini lebih sering membahas tentang operasi perkalian maupun pembagian. Bagaimana rumus perkalian perpangkatan itu? Bagaimana cara menyelesaikan contoh soal perkalian pangkat itu?
Sebelum mempelajari lebih lanjut mengenai rumus perkalian pangkat dan contoh soal perkalian pangkat ini, alangkah lebih baik jika anda memahami terlebih dahulu tentang pengertian perpangkatan. Perpangkatan secara umum dapat diartikan sebagai operasi Matematika yang berisi perkalian bilangan secara berulang sebanyak jumlah pangkatnya. Karena perkalian bilangan tersebut dilakukan secara berulang, maka rumus perkalian bilangan pangkat ini dapat dibuat lebih sederhana sehingga pengerjaannya tidak membutuhkan waktu lama.
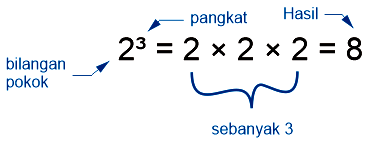
Secara umum pangkat sebuah bilangan dapat diartikan sebagai angka yang penulisannya sedikit ke atas dan ukurannya lebih kecil dibandingkan bilangan pokok itu sendiri. Penulisan huruf berdasarkan semantik ini dapat dinamakan dengan superscript. Misalnya 5⁶, 3⁴, 2⁷ dan sebagainya. Materi perpangkatan tersebut tidak hanya membahas tentang operasi perkalian saja, namun adapula operasi pembagian, pangkat nol, dan pangkat negatif. Bagaimana rumus perkalian bilangan berpangkat itu? Pada kesempatan kali ini saya akan menjelaskan tentang rumus perkalian pangkat dan contoh soal perkalian pangkat. Untuk lebih jelasnya dapat anda simak di bawah ini.
Rumus Perkalian Pangkat dan Contoh Soalnya
Seperti yang telah kita ketahui bahwa bilangan berpangkat adalah sebuah bilangan yang digunakan untuk membuat penulisan menjadi lebih sederhana atau suatu bilangan yang memiliki faktor perkalian sama untuk dapat disebutkan menjadi lebih sederhana. Misalnya 2 x 2 x 2 = …, 4 x 4 x 4 x 4 x 4 = … dan sebagainya. Perkalian bilangan yang memiliki faktor sama ini dapat dinamakan dengan perkalian berulang. Bagaimana jika angka pengalinya banyak? Jika hal ini terjadi maka penulisan angkanya akan lebih sulit. Untuk itulah materi pangkat ini digunakan.
Baca juga : Cara Menghitung Modus, Median, dan Mean Dari Data Tunggal
Bilangan berpangkat memiliki notasi angka yang digunakan untuk menulis setiap perkalian berulang secara ringkas. Misalnya 2 x 2 x 2 menjadi 2³ (dibaca dua pangkat tiga), 4 x 4 x 4 x 4 x 4 menjadi 4⁵ (dibaca empat pangkat 5) dan sebagainya. Sebelum membahas tentang rumus perkalian pangkat dan contoh soal perkalian pangkat tersebut. Saya akan membahas sedikit mengenai bentuk umum perpangkatan terlebih dahulu. Perpangkatan bilangan secara umum dapat ditulis dalam bentuk seperti di bawah ini:
aⁿ = a × a × a × … × a sebanyak n kali
Keterangan:
a = Bilangan pokok (bilangan yang dipangkatkan)
n = eksponen (pangkat), dimana n merupakan bilangan bulat positif
Sifat Sifat Bilangan Berpangkat
Bilangan berpangkat memiliki beberapa sifat di dalamnya. Adapun sifat sifat perpangkatan tersebut yaitu meliputi:
Pangkat Bulat Positif
Sebelum menjelaskan tentang rumus perkalian pangkat dan contoh soal perkalian pangkat tersebut. Saya akan akan membahas terlebih dahulu mengenai sifat bilangan pangkat berupa pangkat bulat positif. Dalam perpangkatan ini terdapat bentuk umum seperti di bawah ini:
aⁿ = a × a × a × … × a
Keterangan:
a = Bilangan pokok (bilangan yang dipangkatkan)
n = eksponen (pangkat)
Baca juga : Cara Menghitung Akar Pangkat 3 Dengan Cepat dan Benar
Dari hasil di atas dapat kita ketahui bahwa n merupakan bilangan bulat positif dan a merupakan bilangan real. Notasi aⁿ ini menjelaskan bahwa bilangan a memiliki hasil sebanyak n faktor.
Catatan:
1. Kita hanya cukup menulis a¹ menjadi a saja.
2. a⁰ tidak semuanya dapat menyatakan 1 untuk kategori bilangan real. Ketika n = 0 dan a = 0, maka hasilnya akan tidak tentu dengan aⁿ = 0⁰.
3. Kita harus memperhatikan semesta variabel jika n adalah sebuah variabel eksponen dari a.
Pangkat bulat negatif ini dapat kita contohkan dalam bentuk seperti 2³ = 2 x 2 x 2 = 8, 3² = 3 x 3 = 9 dan sebagainya.
Pangkat Bulat Negatif
Sebelum menjelaskan tentang rumus perkalian pangkat dan contoh soal perkalian pangkat tersebut. Saya akan akan membahas terlebih dahulu mengenai sifat bilangan pangkat berupa pangkat bulat negatif.
Dalam perpangkatan ini terdapat bentuk umum seperti di bawah ini:
a‾ᵐ = (1/a)ᵐ
Keterangan:
a = Bilangan real, dimana a ≠ 0
m = Bilangan bulat positif
Rumus Perkalian Bilangan Berpangkat
Perkalian perpangkatan dapat dilakukan dengan cara menjumlahkan pangkatnya saja jika bilangan pokoknya sama, baik jumlah bilangannya dua atau lebih. Oleh karena itu rumus perkalian pangkat dapat dinyatakan dalam bentuk seperti berikut:
aᵐ × aⁿ = aᵐ⁺ ⁿ
Agar anda lebih paham mengenai rumus perkalian perpangkatan di atas, maka saya akan membagikan contoh soal perkalian pangkat terkait rumus tersebut. Berikut contoh soal dan jawabannya:
Contoh Soal
Tentukan hasil perpangkatan di bawah ini:
a. 6² x 6⁵
b. (-3)³ x (-3)²
c. (-4)⁵ x (-4)⁴
d. 2² x 3³
e. 2x² x 3x³
Jawaban.
Contoh soal perkalian pangkat ini dapat diselesaikan dengan rumus perkalian pangkat seperti di atas. Untuk itu hasilnya akan seperti di bawah ini:
a. 6² x 6⁵ = 6²⁺⁵ = 6⁷ = 279.936
b. (-3)³ x (-3)² = (-3)³⁺² = (-3)⁵ = -243
c. (-4)⁵ x (-4)⁴ = (-4)⁵⁺⁴ = (-4)⁹ = -262.144
d. 2² x 3³ = tidak dapat disederhanakan karena bilangan pokoknya berbeda yaitu 2 dan 3 sehingga perhitungannya menggunakan cara manual, 2² x 3³ = 4 x 27 = 108.
e. 2y² x 3y³ = (2 x 3)(y)²⁺³ = 6y⁵
Dari hasil pengerjaan di atas dapat kita simpulkan bahwa:
- Bilangan negatif yang berpangkat genap akan menghasilkan bilangan positif.
- Bilangan negatif yang berpangkat ganjil akan menghasilkan bilangan negatif.
Sekian penjelasan mengenai rumus perkalian pangkat dan contoh soal perkalian pangkat. Rumus perkalian bilangan berpangkat di atas dapat berlaku jika bilangan pokoknya sama atau bilangan yang dipangkatkan sama. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.


