6 Macam Pola Bilangan Matematika Beserta Rumusnya – Bilangan ialah sesuatu yang digunakan sebagai sebutan dalam menyatakan jumlah pengukuran atau pecahan. Bilangan tersebut disimbolkan dengan lambang bilangan ataupun angka. Bilangan dalam Matematika memiliki beberapa pola khusus agar dapat dibedakan dengan bilangan lainnya. Pola bilangan Matematika tersebut dapat dibagi menjadi beberapa macam. Bahkan setiap jenis pola bilangan Matematika memiliki rumus pola bilangannya masing masing.
Pola bilangan merupakan bab materi Matematika yang harus dipelajari sebelum materi barisan aritmatika maupun barisan geometri. Hal ini dikarenakan pola bilangan merupakan faktor pendukung siswa agar lebih mudah untuk memahami barisan aritmatika dan geometri. Lalu apa itu pola bilangan? Bagaimana rumus bola bilangan itu? Apa saja macam macam pola bilangan?
Seperti yang telah saya katakan sebelumnya bahwa pola bilangan merupakan dasar dari pembelajaan deret dan barisan aritmatika maupun geometri. Maka dari itu para siswa harus benar benar mengetahui dan memahami apa yang dimaksud pola bilangan tersebut.
6 Macam Pola Bilangan Matematika Beserta Rumusnya
Apa yang dimaksud dengan pola? Apa itu bilangan? Pola ialah model atau bentuk yang mempunyai keteraturan, baik dalam gagasan ataupun desain abstrak. Kemudian bilangan sendiri dapat diartikan sebagai angka angka yang dikumpulkan menjadi satu dengan urutan tempat dari sebelah kanan bernilai satuan, puluhan, ratusan, ribuan dan sebagainya.
Apa yang dimaksud pola bilangan? Pola bilangan ialah susunan dari beberapa bilangan yang membentuk sebuah pola yang teratur. Pola bilangan Matematika ini secara umum dapat dibagi menjadi beberapa macam.
Macam macam pola bilangan tersebut biasanya mengandung rumus tertentu. Adapun jenis jenis pola bilangan Matematika beserta rumus pola bilangannya yaitu:
Baca juga : Rumus Luas Permukaan dan Volume Prisma (Rumus Mudah)
Pola Bilangan Ganjil
Pola bilangan ganjil ialah pola yang dibentuk dari beberapa bilangan ganjil. Bilangan ganjil tersebut memiliki arti yaitu bilangan asli yang tidak dapat dibagi habis oleh bilangan dua ataupun kelipatannya. Adapun bentuk pola bilangan ganjil yaitu:
1, 3, 5, 7, 9, 11, . . .
|
|
| Gambar Pola Bilangan Ganjil |
Rumus Pola Bilangan Ganjil
Untuk menghitung angka pada barisan n pola ganjil dapat menggunakan rumus khusus agar lebih mudah. Berikut rumus pada pola bilangan ganjil suku ke n:
Un = 2n – 1
Contoh Soal
Hitunglah pola bilangan ganjil ke 11 dari barisan bilangan berikut: 1, 3, 5, 7, … , n!
Jawab.
Un = 2n – 1
U11 = 2 (11) – 1
= 22 – 1
= 21
Jadi pola bilangan ganjil ke 11 ialah 21.
Pola Bilangan Genap
Macam pola bilangan Matematika selanjutnya ialah pola bilangan genap. Pola bilangan genap ialah pola yang dibentuk dari beberapa bilangan genap. Bilangan genap tersebut memiliki arti yaitu bilangan asli yang dapat dibagi habis oleh bilangan dua ataupun kelipatannya. Adapun bentuk pola bilangan genapnya :
2, 4, 6, 8, 10, . . .
 |
| Gambar Pola Bilangan Genap |
Rumus Pola Bilangan Genap
Untuk menghitung angka pada barisan n pola genap dapat menggunakan rumus khusus agar lebih mudah. Berikut rumus pada pola bilangan genap suku ke n yaitu:
Un = 2n
Contoh Soal
Hitunglah pola bilangan genap ke 11 dari barisan bilangan berikut: 2, 4, 6, 8, 10, … , n!
Jawab.
Un = 2n
U11 = 2 (11)
= 22
Jadi pola bilangan genap ke 11 ialah 22.
Baca juga : Kumpulan Rumus Matematika SMP Kelas 9 Beserta Penjelasan Lengkap
Pola Bilangan Persegi
Macam pola bilangan Matematika selanjutnya ialah pola bilangan persegi. Pola bilangan persegi ialah pola yang diberasal dari beberapa bilangan hingga membentuk bangun persegi. Berikut bentuk pola bilangan perseginya :
1, 4, 9, 16, 25, 36, . . .
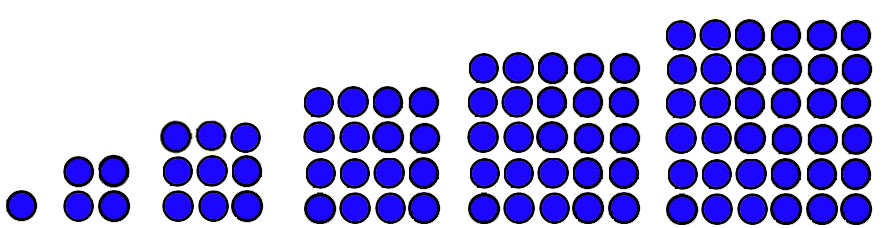 |
| Gambar Pola Bilangan Persegi |
Rumus Pola Bilangan Persegi
Untuk menghitung angka pada barisan n pola persegi dapat menggunakan rumus khusus agar lebih mudah. Berikut rumus pada pola bilangan persegi suku ke n:
Un = n²
Contoh Soal
Hitunglah pola bilangan persegi ke 11 dari barisan bilangan berikut: 1, 4, 9, 16, 25, 36, … , n!
Jawab.
Un = n²
U11 = 11²
= 121
Jadi pola bilangan persegi ke 11 ialah 121.
Pola Bilangan Persegi Panjang
Macam pola bilangan Matematika selanjutnya ialah pola bilangan persegi panjang. Pola bilangan persegi panjang ialah pola yang diberasal dari beberapa bilangan hingga membentuk bangun persegi panjang. Berikut bentuk pola bilangan persegi panjangnya :
2, 6, 12, 20, 30, 42, . . .
 |
| Gambar Pola Bilangan Persegi Panjang |
Rumus Pola Bilangan Persegi Panjang
Untuk menghitung angka pada barisan n pola persegi panjang dapat menggunakan rumus khusus agar lebih mudah. Berikut rumus pola bilangan persegi panjang suku ke n:
Un = n x (n + 1)
Contoh Soal
Hitunglah pola bilangan persegi panjang ke 11 dari barisan bilangan berikut: 2, 6, 12, 20, 30, 42, … , n!
Jawab.
Un = n x (n + 1)
U11 = 11 x (11 + 1)
= 11 x 12
= 132
Jadi pola bilangan persegi panjang ke 11 ialah 132.
Pola Bilangan Segitiga
Macam pola bilangan Matematika selanjutnya ialah pola bilangan segitiga. Pola bilangan segitiga ialah pola yang diberasal dari beberapa bilangan hingga membentuk bangun segitiga. Berikut bentuk pola bilangan segitiganya :
1, 3, 6, 10, 15, 21, . . .
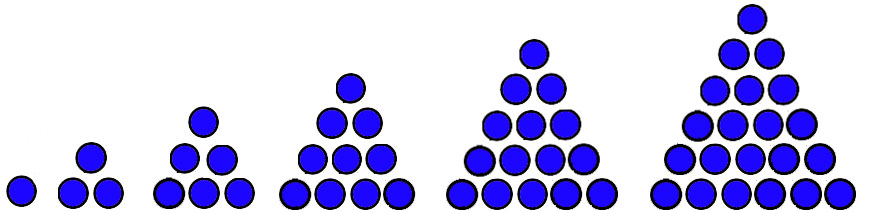 |
| Gambar Pola Bilangan Segitiga |
Baca juga : Rumus Rumus Pangkat (Perkalian, Pembagian, Pangkat Nol dan Negatif)
Rumus Pola Bilangan Segitiga
Untuk menghitung angka pada barisan n pola segitiga dapat menggunakan rumus khusus agar lebih mudah. Berikut rumus pada pola bilangan segitiga suku ke n:
Un = 1/2 n (n + 1)
Contoh Soal
Hitunglah pola bilangan persegi panjang ke 11 dari pola bilangan berikut: 1, 3, 6, 10, 15, 21, … , n!
Jawab.
Un = 1/2 n (n + 1)
U11 = 1/2 x 11 (11 + 1)
= 1/2 x 132
= 66
Jadi pola bilangan segitiga ke 11 ialah 66.
Pola Bilangan Fibonacci
Macam pola bilangan Matematika yang terakhir ialah pola bilangan Fibonacci. Pola bilangan Fibonacci ialah pola yang diperoleh dari jumlah dua suku sebelumnya atau didepannya. Berikut bentuk pola bilangan Fibonacci :
1, 1, 2, 3, 5, 8, 13, 21, 34, 56, . . .
2, 2, 4, 6, 10, 16, 26, 42, 68, 110, . . .
Rumus Pola Bilangan Fibonacci
Untuk menghitung angka pada barisan n pola Fibonacci dapat menggunakan rumus khusus agar lebih mudah. Berikut rumus pola bilangan Fibonacci suku ke n:
Fn = Fn – 1 + Fn – 2, dimana n ≥ 3
F0 = 0 dan F1 = 1
Demikianlah penjelasan mengenai macam macam pola bilangan Matematika beserta rumus pola bilangannya. Pada dasarnya pola bilangan terbentuk dari beberapa barisan bilangan. Hal ini dikarenakan barisan bilangan hampir menyerupai pola bilangan. Namun pola bilangan dimanfaatkan untuk menyelesaikan soal barisan aritmatika maupun barisan geometri. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.



