Cara Menyelesaikan Persamaan Logaritma Beserta Contoh Soal – Logaritma merupakan salah satu materi yang sering menyulitkan siswa. Rumus hitung yang rumit menjadi alasan utama mengapa banyak yang salah ketika menjawab soal. Meski seluruh rumus tertera di buku LKS tapi faktanya kita justru sulit mengaplikasikannya.
Bagaimana cara menyelesaikan contoh soal persamaan logaritma itu? Materi persamaan logartima pada umumnya memang dapat dibagi menjadi beberapa bentuk. Jenis jenis persamaan logaritma tersebut memiliki cara pengerjaan yang berbeda beda. Seperti yang telah kita ketahui bahwa operasi Matematika banyak yang mempunyai pasangan berdasarkan sifat kebalikannya. Contohnya pengurangan dengan penjumlahan, serta pembagian dan perkalian.
Cara Menyelesaikan Persamaan Logaritma Beserta Contoh Soal
Logaritma memiliki kebalikan yang berupa perpangkatan atau eksponen. Meski sering dibahas oleh guru tapi ternyata masih ada beberapa siswa yang belum tau pengertian logaritma. Sehingga saat guru meminta menerapkan cara menyelesaikan persamaan logaritma pun akhirnya mereka kewalahan.
Logaritma secara umum dapat diartikan sebagai operasi Matematika yang berkebalikan dari pemangkatan atau eksponen. Bentuknya pun juga terbilang fleksibel karena bisa berupa bentuk persamaan ataupun pertidaksamaan. Rumus persamaan logaritma sendiri menurut saya sangat efektif untuk mengerjakan beberapa tipe soal.
Apa saja jenis jenis persamaan logaritma itu? Persamaan logaritma memiliki variasi bentuk soal yang berbeda dengan pertidaksamaannya. Untuk itulah cara menyelesaikan pertidaksamaan logaritma berbeda dengan persamaan. Pada kesempatan kali ini saya akan menjelaskan tentang cara menyelesaikan persamaan logaritma beserta contoh soal persamaan logaritma.
Sifat Sifat Persamaan Logaritma
Cara mengerjakan persamaan logaritma sebenarnya sangat mudah apabula kita mengetahui sifatnya. Sehingga, secara tak langsung sifat itu berperan layaknya rumus yang menjadi panutan untuk para siswa. Sifat sifat perasmaan logaritma dipakai untuk menjelaskan hubungan tersebut dalam persamaan dengan nilai yang sama.
Di bawah ini terdapat sifat sifat persamaan logaritma yaitu sebagai berikut:
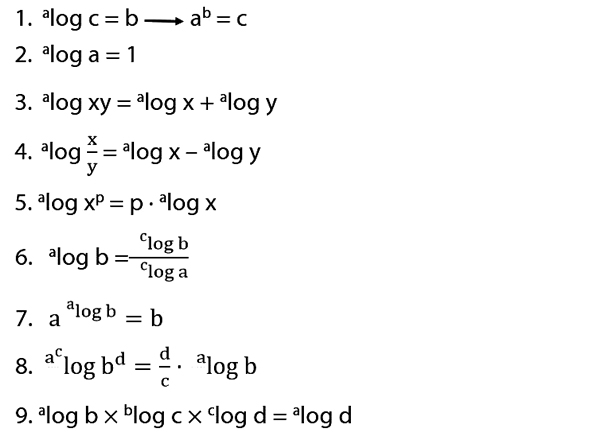
Sifat sifat logaritma di atas dapat digunakan untuk menyelesaikan contoh soal persamaan logaritma yang tersedia. Selain sifat sifat di atas, adapula penjelasan mengenai cara menyelesaikan persamaan logaritma beserta contoh soalnya yaitu:
Baca juga : Contoh Soal Fungsi Komposisi dan Fungsi Invers Beserta Jawaban
Persamaan Logaritma
Seperti yang telah kita ketahui bahwa persamaan logaritma memiliki bentuk dasarnya sendiri. Bentuk dasar persamaan logaritma tersebut dapat berupa:
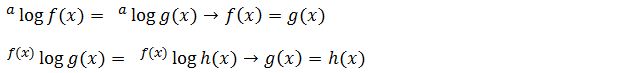
Persamaan logaritma di atas memiliki syarat yaitu h(x) > 0, f(x) > 0 dan g(x) > 0. Dalam materi persamaan logaritma tersebut pada dasarnya terdapat beberapa jenis bentuk persamaan di dalamnya. Berikut jenis jenis persamaan logaritmanya yaitu:
Bentuk Persamaan Logaritma I
Cara menyelesaikan persamaan logaritma yang pertama memiliki bentuk umum seperti berikut ini:
ᵃlog f(x) = ᵃlog b → f(x) = b, dimana f(x) > 0
Agar anda lebih paham mengenai bentuk persamaan logaritma yang pertama ini, maka saya akan membagikan contoh soal terkait bentuk tersebut. Berikut contoh soal persamaan logaritma bentuk I yaitu:
Tentukan penyelesaian dari ³log 4x² – x = 1?
Pembahasan.
³log 4x² – x = 1
³log 4x² – x = ³log 3
4x² – x = 3
4x² – x – 3 = 0
(-4x – 3)(-x + 1) = 0
-4x – 3 = 0 atau -x + 1 = 0
x = -¾ atau x = 1
Bentuk Persamaan Logaritma II
Cara menyelesaikan persamaan logaritma selanjutnya memiliki bentuk umum seperti berikut ini:
ᵃlog f(x) = ᵇlog f(x) → f(x) = 1, dimana a ≠ b
Agar anda lebih paham mengenai bentuk persamaan logaritma yang kedua ini, maka saya akan membagikan contoh soal terkait bentuk tersebut. Berikut contoh soal persamaan logaritma bentuk II yaitu:
Baca juga : Contoh Soal Luas dan Keliling Lingkaran Beserta Pembahasannya
Tentukan nilai x yang memenuhi persamaan logaritma di bawah ini!
²log (3x² – 6x – 8) = ³log (3x² – 6x – 8)
Pembahasan.
²log (3x² – 6x – 8) = ³log (3x² – 6x – 8)
3x² – 6x – 8 = 1
3x² – 6x – 9 = 0
(3x – 9)(x + 1) = 0
3x – 9 = 0 atau x + 1 = 0
3x = 9 x = -1
x = 3
Bentuk Persamaan Logaritma III
Cara menyelesaikan persamaan logaritma selanjutnya memiliki bentuk umum seperti berikut ini:
ᵃlog f(x) = ᵃlog g(x) → f(x) = g(x), dimana f(x) > 0 dan g(x) > 0
Agar anda lebih paham mengenai bentuk persamaan logaritma yang ketiga ini, maka saya akan membagikan contoh soal terkait bentuk tersebut. Berikut contoh soal persamaan logaritma bentuk III yaitu:
Tentukan nilai x yang memenuhi persamaan logaritma di bawah ini!
⁵log (3x² + 6x – 11) = ⁵log (x² – 5x + 19)
Pembahasan.
⁵log (3x² + 6x – 11) = ⁵log (x² – 5x + 19)
3x² + 6x – 11 = x² – 5x + 19
3x² + 6x – 11 – x² + 5x – 19 = 0
2x² + 11x – 30 = 0
(2x + 15)(x – 2) = 0
2x + 15 = 0 atau x – 2 = 0
2x = -15 x = 2
x = -15/2
Bentuk Persamaan Logaritma IV
Cara menyelesaikan persamaan logaritma selanjutnya memiliki bentuk umum seperti berikut ini:
![]()
Keterangan:
f(x) > 1, g(x) > 0 dan h(x) > 0
Agar anda lebih paham mengenai bentuk persamaan logaritma yang ke empat ini, maka saya akan membagikan contoh soal terkait bentuk tersebut. Berikut contoh soal persamaan logaritma bentuk IV yaitu:
Tentukan nilai x yang memenuhi persamaan logaritma di bawah ini!![]()
Pembahasan.![]()
Maka.
3x² – 4x + 21 = x² + 7x + 6
3x² – 4x + 21 – x² – 7x – 6 = 0
2x² – 11x + 15 = 0
(2x – 5)(x – 3) = 0
2x – 5 = 0 atau x – 3 = 0
x = 5/2 x = 3
Demikianlah penjelasan mengenai cara menyelesaikan persamaan logaritma beserta contoh soal persamaan logaritma. Persamaan logaritma pada umumnya dapat dibagi menjadi beberapa jenis seperti di atas, dimana memiliki bentuk dasar yang berbeda beda. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi persamaan logaritma di atas.


