Materi Diagram Venn (Pengertian, Bentuk dan Contoh Soal) – Buatlah diagram venn antara pasar tradisional dan pasar modern! tak semua siswa mampu menjawabnya. Faktanya, masih banyak yang tak mengetahui apa pengertian serta contoh diagram venn itu bagiamana bentuknya. Hal inilah yang terkadang menjadi kendala siswa pada saat mengerjakan soal ujain.
Nama diagram ini diperoleh dari nama belakang penemunya yaitu Jhon Venn. Diagram venn adalah jenis diagram yang menggambarkan adanya beberapa himpunan yang tergabung dalam himpunan semesta. Dari pengertian ini dapat kita lihat bahwa diagram venn tersebut berhubungan dengan adanya himpunan tertentu yang dikumpulkan menjadi satu semesta tertentu.
Beberapa ahli juga mendefinisikan diagram venn sebagai media untuk menjelaskan hubungan persamaan himpunan yang dikelompokan menjadi objek tertentu. Secara garis besar fungsinya adalah untuk menjelaskan drbush himpunan saling lepas, berpotonga, dan lain-lain. Kita bisa menjumpai berbagai contoh soal diagram venn dengan mudah di buku pedoman matematika. Secara intensif, guru pun pasti akan menjelaskan contoh diagram venn sebagai bentuk pendalaman materi.
Materi Diagram Venn (Pengertian, Bentuk dan Contoh Soal)
Seperti yang telah saya katakan bahwa diagram venn berhubungan dengan himpunan. Apa pengertian himpunan itu? Himpunan ialah objek yang dikumpulkan menjadi satu untuk dinyatakan secara jelas. Misalnya sekarang ini anda menggunakan pakaian, maka termasuk dalam himpunan yang terdiri dari baju, celana, jaket, topi dan lain lain.Himpunan tersebut penulisannya berada di dalam tanda kurung. Contohnya {baju, celana, jaket, topi, . . .}.
Contoh diagram venn biasanya berisi beberapa himpunan yang terkumpul menjadi satu. Materi tersebut mulai diperkenalkan saat siswa berada di bangku kelas 7 SMP. Dalam penjelasan tersebut terdapat pembahasan mengenai diagram venn gabungan, diagram venn komplemen, pengertian diagram venn dan contohnya serta masih banyak lagi. Diagram venn dapat didefinisikan sebagai gambar yang berguna dalam menjelaskan hubungan sekelompok objek dalam himpunan dengan persamaan jumlah dan nilai.
Baca juga : Materi Limit Fungsi Aljabar Beserta Rumus dan Contoh Soalnya
Selain itu diagram venn berguna untuk menyatakan adanya fraksi, persimpangan dan lain lain. Diagram tersebut digunakan dalam aplikasi komputer, Matematika dan statistik dalam bentuk sajian teknik serta data ilmiah. Cara membuat diagram venn tersebut dapat dilakukan dengan cara memahami jumlah himpunannya terlebih dahulu. Selain itu anda juga harus memahami juga tentang pengertian diagram venn, bentuk bentuk diagram venn dan cara menyelesaikan diagram venn tersebut.
Contoh Diagram Venn
Perhatikan gambar di bawah ini untuk memahami cara menggambar diagram venn yang baik dan benar yaitu sebagai berikut:
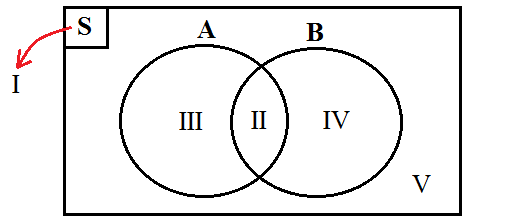
Dalam gambar diatas terdapat beberapa komponen didalamnya seperti himpunan semesta (dilambangkan dengan angka I atau huruf S), anggota irisan himpunan A dan B (angka II), anggota himpunan A saja (angka III), anggota himpunan B saja (angka IV), dan anggota diluar himpunan A dan B (angka V). Di bawah ini terdapat beberapa cara membuat diagram venn yaitu sebagai berikut:
- Dalam diagram venn terdapat himpunan semesta digambarkan dalam bentuk persegi panjang.
- Penyampaian masing masing himpunan akan dijelaskan dalam bentuk kurva tertutup atau lingkaran.
- Sebuah titik merupakan perwakilan dari masing masing anggota himpunan.
Ciri Ciri Diagram Venn
Dalam materi diagram venn tidak hanya menjelaskan tentang pengertian diagram venn dan cara membuat diagram venn tersebut. Selanjutnya saya akan membahas tentang ciri ciri diagram venn. Diagram venn memiliki beberapa ciri ciri didalamnya seperti:
- Memiliki himpunan semesta yang digunakan untuk menjelaskan nilai atau data total yang sedang dibahas.
- Memiliki daerah yang termasuk dalam himpunan A maupun himpunan B (A∩B).
- Memiliki anggota himpunan A saja yang banyak, tanpa disertai dengan himpunan B.
- Memiliki anggota himpunan B saja yang banyak, tanpa disertai dengan himpunan A.
- Memiliki anggota himpunan semesta yang banyak, tetapi tidak termasuk dalam anggota himpunan A maupun B.
Bentuk Bentuk Diagram Venn
Setelah menjelaskan tentang ciri ciri diagram venn di atas, selanjutnya saya akan membahas tentang macam atau bentuk bentuk diagram venn. Bentuk dari diagram venn tersebut pada umumnya tidak sama. Berikut penjelasan selengkapnya:
Baca juga : Rumus Perkalian Matriks dan Perkalian Skalar Matriks Lengkap
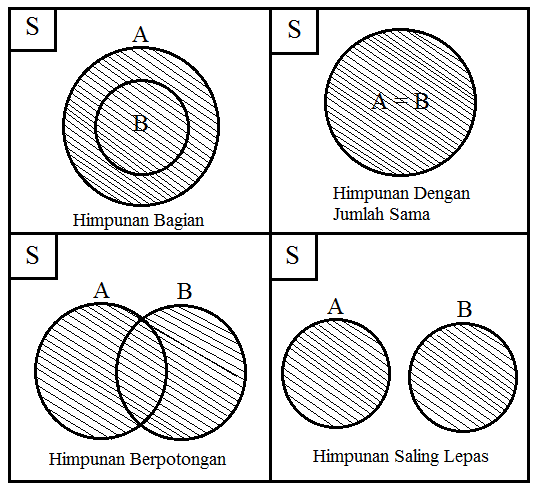
Himpunan Bagian
Bentuk dalam materi diagram venn yang pertama ialah himpunan bagian. Apabila anggota A semuanya ialah anggota B, maka dapat dinyatakan bahwa A himpunan bagian dari himpunan B.
Himpunan Jumlah Sama
Jenis diagram venn selanjutnya ialah himpunan jumlah sama. Masing masing anggota B ialah anggota A, jika terdapat persamaan set dalam himpunan A dan himpunan B. Misalnya A = {1, 2, 3} dan B ={3, 2, 1}. A dan B dapat ditulis menjadi A = B karena anggota himpunannya sama.
Himpunan Berpotongan
Bentuk diagram venn selanjutnya ialah himpunan berpotongan. Apabila kedua himpunan mempunyai persamaan, maka dapat dinyatakan sebagai dua himpunan berpotongan dalam diagram venn. Contohnya himpunan A berpotongan dengan himpunan B dalam diagram venn, maka diantara keduanya memiliki persamaan. Dengan kata lain dalam himpunan A terdapat anggota yang sama dengan milik himpunan B. Lambang berpotongan pada anggota himpunan A dan himpunan B dapat berupa A∩B.
Himpunan Saling Lepas
Macam diagram venn selanjutnya ialah himpunan saling lepas. Apabila himpunan A memiliki anggota yang berbeda dengan anggota pada himpunan B, maka dapat dinyatakan bahwa himpunan A tidak saling tergantung dengan himpunan B. Hal ini dapat ditulis dalam materi diagram venn yang berbentuk A // B.
Himpunan Ekuivalen
Bentuk diagram venn selanjutnya ialah himpunan ekuivalen. Apabila terdapat persamaan jumlah dalam anggota himpunan A dan B, maka dapat dinyatakan bahwa keduanya setara. Penulisan himpunan A yang setara dengan himpunan B dapat berbentuk n(A) = n(B).
Baca juga : Kumpulan Soal Logaritma Beserta Jawabannya Lengkap
Selain pengertian diagram venn dan bentuk bentuk dalam diagram venn di atas. Adapula beberapa hubungan yang terjadi antar himpunan. Hubungan beberapa himpunan ini dapat berupa selisih, irisan, gabungan dan komplemen himpunan. Adapun penjelasan selengkapnya yaitu sebagai berikut:
Gabungan
Hubungan antar himpunan yang pertama ialah gabungan. Gabungan himpunan A dengan himpunan B merupakan ketetapan anggota yang jumlahnya menuju anggota himpunan A, B atau keduanya (A dan B). Hasil himpunan A yang dikombinasikan dengan B dapat ditulis A ∪ B = {x | x ∈ A atau x ∈ B}. Untuk lebih jelasnya dapat anda simak contoh soal diagram venn gabungan seperti di bawah ini:
Diketahui himpunan A = {2, 4, 6, 8, 10, 12} dan himpunan B = {1, 2, 3, 4, 5}. Buatlah diagram venn pada kedua himpunan tersebut!
Jawab.
Himpunan A = {2, 4, 6, 8, 10, 12}
Himpunan B = {1, 2, 3, 4, 5}
A ∪ B = {1, 2, 3, 4, 5, 6, 8, 10, 12}
Gambar diagram venn nya akan menjadi seperti di bawah ini:
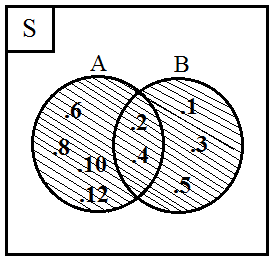
Irisan
Materi diagram venn selanjutnya membahas tentang hubungan antar himpunan yang berupa irisan atau bagian. Himpunan bagian A dengan B merupakan anggota himpunan A yang termasuk dalam himpunan B. Irisan himpunan A dan B dapat ditulis menjadi A∩B. Untuk lebih jelasnya dapat anda simak contoh soal diagram venn irisan seperti di bawah ini:

Berdasarkan gambar di atas dapat simpulkan beberapa hal seperti:
Himpunan A = {2, 4, 6, 8, 10, 12}
Himpunan B = {1, 2, 3, 4, 5}
A∩B = {2, 4}
Komplemen
Hubungan antar himpunan selanjutnya ialah komplemen. Komplemen atau himpunan tambahan A ialah banyaknya anggota dalam himpunan universal, namun tidak termasuk dalam himpunan anggota A. Komplemen ini dapat ditulis Ac. Untuk lebih jelasnya dapat anda simak contoh diagram venn komplemen di bawah ini:
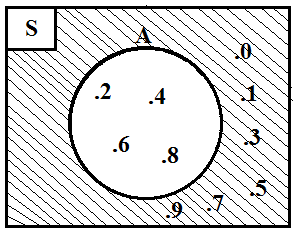
Berdasarkan gambar diagram venn di atas dapat diketahui bahwa himpunan A = {2, 4, 6, 8} dan himpunan S = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Kemudian adapula komplemen himpunan A yang dapat ditulis berbentuk Ac = {0, 1, 3, 5, 7, 9}.
Demikianlah penjelasan mengenai materi diagram venn yang terdiri dari pengertian diagram venn, bentuk bentuk diagram venn dan contoh soal diagram venn. Diagram venn ialah diagram yang menggambarkan adanya beberapa himpunan yang tergabung dalam himpunan semesta. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.