Rumus Invers Matriks Beserta Contoh Soal Matriks – Matriks merupakan salah satu materi pembelajaran Matematika yang terdiri dari susunan bilangan yang berada pada sebuah kurung. Sedangkan menurut para ahli, Matriks diartikan sebagai sekumpulan bilangan yang tersusun sedemikian rupa dalam bentuk baris dan kolom serta berada dalam kurung siku ataupun kurung biasa. Materi matriks tersebut terbagi menjadi beberapa macam seperti invers matriks, determinan matriks, adjoin matriks dan sebagainya.
Dari sekian jenis materi pada matriks tersebut terdapat salah satu materi yang cukup banyak dicari yaitu rumus invers matriks dan contoh soal matriks invers itu sendiri. Sebenarnya kita bisa menemukan materi yang berisi rumus invers ataupun perkalian matriks pada mata pelajaran matematika di sekolah menengah. Namun faktanya masih ada banyak siswa yang merasa kesulitan dalam mempelajari rumus tentang invers matriks tersebut.
 |
| Matriks |
Penggunaan kata invers dalam materi matriks tersebut sering ditemukan dalam aljabar yang artinya adalah kebalikan (inversi). Jadi invers dari 3 adalah 1/3 .Untuk itu invers dari bilangan rasional a ialah 1/a. Hal ini tentunya berlaku juga untuk matriks. Namun dalam matriks terdapat rumus tersendiri untuk menghitung inversnya. Rumus invers tersebut dapat dikategorikan menjadi dua jenis yaitu rumus untuk ordo 2×2 dan rumus untuk ordo 3×3. Nah dalam pembahasan kali ini saya akan menjelaskan tentang rumus invers matriks ordo 2×2 dan ordo 3×3 beserta contoh soal invers matriksnya.
Rumus Invers Matriks Beserta Contoh Soal Matriks
Soal matriks memang dianggap sulit oleh sebagian siswa. Banyak yang gagal dan membuang waktu mengerjakannya ketika ujian berlangsung. Siswa dituntut harus hafal sifat sifat matriks itu sendiri sebelum menentukan rumus hitungnya.
Guru biasanya akan menyampaikan materi satu ini ketika kita menginjak bangku SMA atau SMK. Cakupan pembahasan yang terdiri dari rumus dan sifat matriks pun bisa kita baca secara mandiri di buku pedoman matematika. Sayangnya, beberapa siswa masih merasa kesulitan dan kehabisan waktu ketika mengerjakan ujian. Maka dari itu kalian perlu mencari alternatif metode baru agar bisa menyelesaikan soal invers matriks lebih cepat.
Dalam pengerjaannya, kita akan menemukan berbagai contoh soal seperti perkalian invers matriks 3×3 atapun invers matriks 2×2 hingga invers matriks 4×4. Namun sebenarnya metode dan cara mengerjakan soal matriks tersebut tidak jauh berbeda asalkan kita sudah paham rumus pada invers matriks itu sendiri. Lalu bagaimana kita bisa mempelajari rumus matriks dengan cepat?
Rumus dan Sifat Invers Matriks
Invers pada matriks dilambangkan dengan nama tertentu seperti huruf kapital kemudian dipangkatkan dengan -1. Misalnya diketahui matriks B, maka invers matriks B nya dapat ditulis B‾¹. Sebelum saya membahas tentang rumus invers matriks ordo 2×2 dan ordo 3×3 beserta contoh soal invers matriksnya. Saya akan membagikan beberapa sifat dari invers terlebih dahulu. Adapun sifat sifat invers matriks yaitu sebagai berikut:
- AA‾¹ = A‾¹A= I
- (AB)‾¹ = B‾¹A‾¹
- (A‾¹)‾¹ = A
- Jika XA = B, maka X = BA‾¹
- Jika AX = b, maka X =A‾¹B
Baca juga : Cara Menghitung Besar Sampel Dengan Rumus Slovin
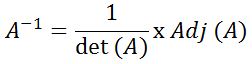 |
| Rumus Invers Matriks |
Keterangan :
A‾¹ = Invers Matriks (A)
det (A) = Determinan Matriks (A)
Adj (A) = Adjoin Matriks (A)
Mampu menghafal rumus invers matriks memang menjadi modal awal siswa untuk mengerjakan soal ujian. Tapi faktanya masih banyak siswa kesulitan ketika mencoba menyelesaikan beberapa bentuk matriks tersebut. Hal ini disebabkan karena perbedaan bilangan yang ada antara di buku latihan dan soal aslinya.
Invers Matriks 2×2
Secara garis besar, rumus invers matriks 2×2 cukup sederhana karena hanya ada 4 bilangan saja yang ada dalam kurung. Secara otomatis, cara mengerjakan invers matriks 2×2 tentunya lebih mudah kita kita bandingan dengan ordo 3×3. Kalian bisa mengerjakan dan menghitungnya secara cepat untuk menghemat waktu ketika ujian.
Nah, pada sesi ini saya ingin membagikan rumus matriks 2×2 yang notabenya hanya dapat dipakai untuk bentuk ini saja. Kalian tak bisa mengaplikasikannya pada ordo 3×3. Tapi, sebelum itu kita harus mencari nilai adjoin matriksnya terlebih dahulu. Untuk lebih jelasnya dapat anda simak contoh di bawah ini.
Contoh Soal Invers Matriks 2×2
Tentukan invers matriks dari ![]() !
!
Jawab.
Untuk menghitung invers matriks tersebut, cara yang digunakan ialah cara cepat. Sebelum menggunakan rumus invers matriks di atas. Kita harus mencari nilai adjoin nya terlebih dahulu.
Dalam mencari adjoin invers matriks 2×2, kita hanya perlu menukar atau memindahkan elemen yang posisinya di baris pertama kolom pertama dengan elemen di baris kedua kolom kedua. Setelah itu baris kedua kolom pertama dan baris pertama kolom kedua dikali dengan -1. Maka hasilnya akan menjadi seperti di bawah ini.
| Mencari Adjoin Invers Matriks 2×2 |
Setelah itu mencari determinan matriksnya dengan cara biasa yaitu
det = (2 x 6) – (4 x 1)
= 12 – 4
= 8
Baca juga : Materi Kesebangunan Bangun Datar (Pengertian, Rumus, dan Contoh)
Setelah adjoin dan determinan matriksnya diketahui. Lalu masukkan ke dalam rumus invers matriks di atas. Maka hasilnya akan seperti di bawah ini:
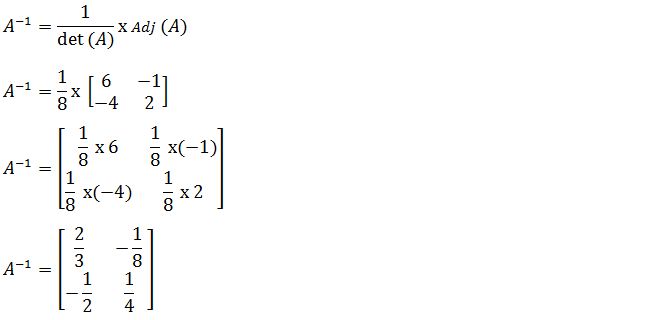 |
| Jawaban Contoh Soal Invers Matriks 2×2 |
Invers Matriks 3×3
Secara garis besar rumus invers matriks 3×3 hampir sama seperti ordo sebelumnya. Namun perbedaannya terletak pada jumlah bilangan dalam kurung yang berjumlah 9. Oleh karena itu, cara menyelesaikan invers matriks tersebut membutuhkan waktu lebih lama dari biasanya.
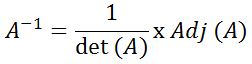 |
| Rumus Invers Matriks |
Seperti sebelumnya kalian harus mencari determinan terlebih dahulu sebelum mulai mencari perkailan matriks 3×3. Dalam buku pedoman matematika telah dijelaskan dua metode utama yang dapat kalian pakai untuk mencari determinan. Diantaranya adalah:
- Metode Sarrus
- Metode Minor-Kofaktor
Namun biasanya determinan invers matriks 3×3 akan lebih mudah dihitung menggunakan metode sarrus. Adapun caranya yaitu sebagai berikut:
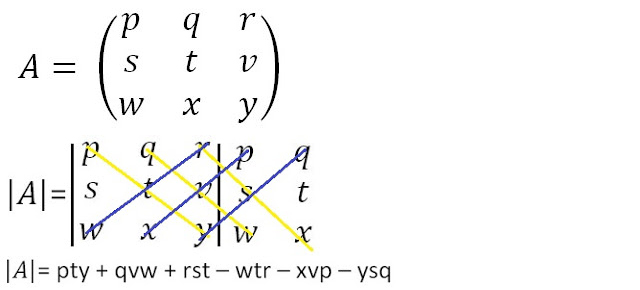 |
| Cara Mencari Determinan Matriks 3×3 |
Setelah itu kita mencari adjoin matriks dalam rumus invers matriks. Untuk menghitung adjoin matriks, kita harus mencari nilai matriks kofaktornya terlebih dahulu. Matriks kofaktor ialah matriks yang elemennya diubah dengan nilai determinan yang nilainya tidak sekolom dan tidak sebaris dengan elemen asal. Setelah itu secara bergantian tinggal diberikan tanda positif atau negatif seperti di bawah ini:
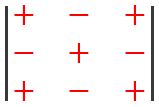 |
| Pemberian tanda pada Adjoin Matriks 3×3 |
Agar anda lebih memahami mengenai rumus pada invers matriks 3×3 tersebut. Saya akan membagikan contoh soal terkait rumus invers ini. Berikut contoh soal invers matriksnya:
Contoh Soal Invers Matriks 3×3
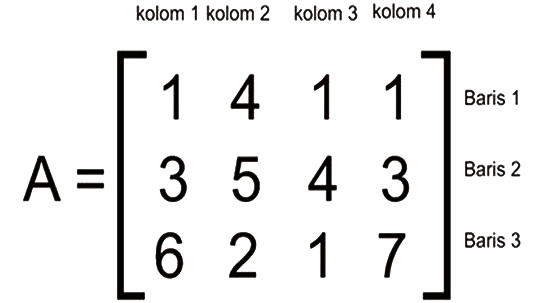
Diketahui matriks A seperti di bawah ini:

Tentukan Invers matriks A di atas!
Baca juga : Rumus dan Contoh Pertidaksamaan Linear Satu Variabel
 |
| Jawaban Contoh Soal Invers Matriks 3×3 |
Sekian penjelasan mengenai rumus invers matriks dan contoh soal invers matriks yang dapat saya sampaikan dalam artikel kali ini. Sebenarnya dalam mengerjakan berbagai soal matriks sangatlah mudah, yang kita perlukan adalah lebih banyak praktek latihan soal dan menghafal setiap rumus perkalian matriks tersebut. Satu hal lagi yang harus kita ingat adalah untuk mencari perkalian invers matriks, kita harus mencari determinan dan adjoin matriksnya terlebih dahulu, hal tersebut adalah rumus pada invers matriks yang bisa dikatakan mutlak.


Materinya bagus mbak, tapi saya mau berkomnetar sedikit. Contoh matriks ordo 3×3 itu jika hasil determinannya nol maka matriks tersebut tidak memiliki invers, karena jika kita memasukkan ke rumus invers, 1 per 0 maka hasilnya tidak terdefinisi.
Sukses trs mba ^-^