Cara Mencari Tinggi Tabung, Rumus, dan Contoh Soalnya – Seperti yang kita tahu bahwa dalam Matematika terdapat pembahasan mengenai bangun ruang. Salah satu jenis bangun ruang yang akan kita bahas adalah bangun tabung. Bangun ruang ini sering kali muncul dalam soal soal Matematika. Tabung memiliki karakeristiknya sendiri seperti halnya jenis bangun ruang lainnya. Bangun tabung memiliki tiga sisi yang berupa sisi selimut berbentuk persegi panjang dan dua lingkaran di bagian tutup dan alas tabung.
Apa itu tabung? Tabung dapat diartikan sebgai bentuk khusus dari prisma tegak yang sisinya diperbanyak pada bidang alasnya sehingga bentuknya menjadi lingkaran. Bangun tabung ini pada umumnya dapat kita jumpai dalam berbagai jenis benda disekitar seperti ember, pipa, botol, kaleng, gelas, toples, drum minyak dan sebagainya. Jika membahas tentang tabung, maka tidak dapat dilepaskan dari adanya rumus tinggi tabung, cara mencari tinggi tabung dan contoh soal tinggi tabung.
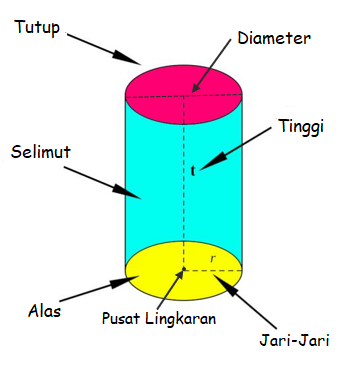
Tabung memang berbeda dengan jenis bangun ruang lainnya. Ha ini dikarenakan tabung mempunyai tinggi, namun tidak memiliki titik sudut. Maka dari itu bentuk kedua sisi tutup dan alasnya adalah lingkaran. Bagaimana cara mencari tinggi tabung itu? Pada kesempatan kali ini saya akan menjelaskan tentang rumus tinggi tabung dan contoh soal tinggi tabung. Untuk lebih jelasnya dapat anda simak di bawah ini.
Cara Mencari Tinggi Tabung, Rumus, dan Contoh Soalnya
Seperti yang kita tahu bahwa tinggi tabung merupakan unsur tabung yang bentuknya garis yang tegak lurus dengan tutup dan alasnya. Dalam tabung ini adapula penggunaan phi dalam perhitungan besar tutup dan alas tabung tersebut. Lantas apa yang dimaksud tabung itu?
Silinder atau tabung merupakan bangun ruang tiga dimensi yang berasal dari satu persegi panjang yang mengelilingi selimut tabung dan dua lingkaran yang saling sejajar. Tabung mempunyai 2 rusuk dan 3 sisi. Bentuk sisi tutup dan alasnya adalah lingkaran serta selimut tabung yang menyelimutinya. Materi tabung ini pada umumnya telah diajarkan ketika di bangku sekolah. Materi ini berisi cara mencari tinggi tabung, rumus dan contoh soal di dalamnya.
Baca juga : Sewindu Berapa Tahun? Jawaban dan Contoh Soalnya
Bangun ruang tabung memiliki 3 sisi yakni sisi atas, sisi bawah, dan sisi lengkung. Agar anda lebih paham mengenai cara mencari, rumus tinggi tabung dan contoh soal tinggi tabung tersebut. Maka saya akan menjelaskan tetang cara mencari rumus tabung seperti di bawah ini:
Rumus Tinggi Tabung Jika Diketahui Volume dan Jari jari
Tinggi tabung dapat diperoleh dengan menggunakan rumus volumenya. Tabung memiliki volume yang merupakan ukuran jumlah ruang atau kapasitas tabung yang ditempatinya. Adapun rumus tabung yang dapat digunakan untuk mencari tinggi tabung yaitu sebagai berikut:
V = π x r² x t
t = V/( π x r²)
Keterangan:
V =Volume tabung (m³)
π= phi (3,14 atau 22/7)
r= Jari jari tabung (m)
t= Tinggi tabung (m)
Rumus Tinggi Tabung Jika Diketahui Luas Permukaan dan Jari Jari
Cara mencari tinggi tabung jika diketahui luas permukaan dan jari jarinya dapat dilakukan dengan menggunakan rumus tertentu. Apa itu luas permukaan tabung? Luas permukaan tabung adalah dua kali luas alas tabung yang semakin bertambah bentuknya dengan bentuk lingkaran dari luas selimutnya. Adapun cara mencari rumus tinggi tabung yaitu sebagai berikut:
L = (2 x π r²) + 2 πrt
L = 2πr (r+t)
(r+t) = L/2πr
t = (L/2πr) – r
Keterangan:
L = Luas permukaan tabung (m²)
π= phi (3,14 atau 22/7)
r= Jari jari tabung (m)
t= Tinggi tabung (m)
Baca juga : Rumus Persamaan Garis Singgung Lingkaran Beserta Contoh Soal
Rumus Tinggi Tabung Jika Diketahui Luas Selimut dan Jari Jari
Cara mencari tinggi tabung jika diketahui luas selimut dan jari jarinya dapat dilakukan dengan menggunakan rumus tertentu. Apa itu selimut tabung? Pengertian selimut tabung adalah persegi yang digulung hingga bentuknya silinder. Adapun cara mencari rumus tinggi tabung yaitu sebagai berikut:
Ls = 2πrt
t = Ls/2πr
Keterangan:
Ls = Luas selimut tabung (m²)
π= phi (3,14 atau 22/7)
r= Jari jari tabung (m)
t= Tinggi tabung (m)
Contoh Soal Tinggi Tabung
Setelah menjelaskan tentang rumus tinggi tabung di atas. Selanjutnya saya akan membagikan contoh soal cara mencari tinggi tabung yaitu meliputi:
1. Diketahui tabung memiliki volume 25.872 cm³ dengan jari jari 14 cm. Tentukan tinggi tabung tersebut? (π = 22/7)
Pembahasan.
Diketahui : V = 25.872 cm³; r = 14 cm; π = 22/7
Ditanyakan : t = ?
Jawab :
Contoh soal tinggi tabung ini dapat diselesaikan dengan rumus seperti di bawah ini:
t = V / ( π x r²)
t = 25.872 / (22/7 x 14²)
t = 25.872 / 616
t = 42 cm
Jadi tinggi tabung tersebut adalah 42 cm.
2. Diketahui tabung memiliki luas selimut 1.256 cm² dengan jari jari 10 cm. Tentukan tinggi tabung tersebut? (π = 3,14)
Pembahasan.
Diketahui : L = 1.256 cm²; r = 10 cm; π = 3,14
Ditanyakan : t = ?
Jawab :
Contoh soal tinggi tabung ini dapat diselesaikan dengan rumus seperti di bawah ini:
t = Ls/2πr
t = 1.256 / (2 x 3,14 x 10)
t = 1.256 / 62,8
t = 20 cm
Jadi tinggi tabung tersebut adalah 20 cm.
Demikianlah penjelasan mengenai rumus tinggi tabung dan contoh soal tinggi tabung. Cara mencari tinggi tabung dapat dilakukan dengan menggunakan rumus tertentu sesuai dengan unsur tabung yang diketahui. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.