Rangkuman Materi Fungsi Kuadrat Matematika Beserta Contoh Soal – Matematika merupakan salah satu jenis pelajaran yang dianggap cukup sulit untuk dipahami. Hal ini dikarenakan penerimaan pelajaran Matematika didasarkan pada kemauan belajar dalam diri sendiri manusia. Terlebih lagi kemampuan yang dimiliki oleh masing masing manusia juga berbeda beda
Pelajaran Matematika terdiri dari beberapa materi didalamnya. Salah satunya ialah materi fungsi kuadrat. Dalam materi Matematika ini mencakup beberapa hal yang dibahas seperti rumus fungsi kuadrat, contoh soal fungsi kuadrat dan sebagainya. Apakah anda tahu bagaimana cara menyelesaian soal soal materi fungsi kuadrat Matematika itu?
Pengertian fungsi kuadrat secara umum ialah sebuah fungsi yang memiliki variabel pangkat besar seperti 2. Materi fungsi kuadrat Matematika ini hampir sama dengan persamaan kuadrat, tetapi yang membedakannya ialah bentuk fungsinya.
Bagaimana rangkuman materi fungsi kuadrat Matematika itu? Bentuk umum fungsi kuadrat sendiri dapat berupa ![]() , dimana a ≠ 0 dan a, b, c merupakan bilangan real. Misalnya f(x) = 2x² + 4x + 7. Untuk itu diperoleh f(2) = 2(2)² + 4(2) + 7 = 23, f(3) = 2(3)² + 4(3) + 7 = 37 dan sebagainya. Bentuk umum fungsi tersebut dapat menjadi dasar rumus fungsi kuadrat Matematika. Rumus tersebut digunakan untuk menyelesaikan contoh soal fungsi kuadrat Matematika.
, dimana a ≠ 0 dan a, b, c merupakan bilangan real. Misalnya f(x) = 2x² + 4x + 7. Untuk itu diperoleh f(2) = 2(2)² + 4(2) + 7 = 23, f(3) = 2(3)² + 4(3) + 7 = 37 dan sebagainya. Bentuk umum fungsi tersebut dapat menjadi dasar rumus fungsi kuadrat Matematika. Rumus tersebut digunakan untuk menyelesaikan contoh soal fungsi kuadrat Matematika.
Rangkuman Materi Fungsi Kuadrat Matematika Beserta Contoh Soal
Pengertian fungsi kuadrat ialah suatu fungsi polinom yang mempunyai variabel atau peubah dengan pangkat paling tinggi berupa dua. Materi Matematika ini digunakan sebagai bahan bahan soal ujian, baik ujian Nasional maupun ujian Sekolah. Dalam bentuk umum f(x) = ax² + bx + c tersebut terdapat sebuah konstanta yang dinyatakan dalam huruf a, b, dan c, serta x merupakan variabel bebas.
Meskipun hampir mirip dengan persamaan kuadrat namun keduanya pada umumnya berbeda. Dalam persamaan kuadrat memiliki bentuk persamaan dan memiliki pangkat tertinggi berupa dua. Pada kesempatan kali ini saya akan membagikan rangkuman rumus fungsi kuadrat Matematika beserta contoh soal fungsi kuadrat.
Persamaan kuadrat memiliki bentuk umum ax² + bx + c =0, dimana a ≠ 0. Dari persamaan ini tentunya keduanya berbeda. Dalam materi fungsi kuadrat Matematika pada umumnya berhubungan dengan grafik fungsi. Hal ini dikarenakan grafik fungsi memiliki kaitan yang erat dengan sebuah fungsi.
Baca juga : Contoh Soal Notasi Sigma Kelas 11 Beserta Jawabannya
Seperti yang telah saya jelaskan di atas bahwa pengertian fungsi kuadrat ialah sebuah fungsi polinom yang memliki peubah atau variabel dengan pangkat paling tinggi berupa 2. Bentuk umum fungsi kuadrat dapat berupa f(x) = ax² + bx + c atau y = ax² + bx + c. Selain itu adapula bentuk grafik fungsi yang berupa parabola. Grafik materi fungsi kuadrat Matematika ini menggunakan titik ekstrim dan sumbu koordinat dalam penentuan titik potongnya.
Titik Potong dengan Sumbu Koordinat
Titik ekstrim dalam fungsi kuadrat dapat dinamakan dengan titik minimum/maksimum atau titik puncak. Selain itu adapula titik potong dengan sumbu koordinat yang terdapat dalam rangkuman materi fungsi kuadrat Matematika. Kedua hal ini tidak dapat dilepaskan dari adanya fungsi kuadrat. Bahkan pembuatan grafik fungsi kuadratnya juga berhubungan dengan hal hal tersebut.
Rangkuman fungsi kuadrat Matematika yang pertama membahas tentang titik potong pada sumbu koordinat. Cara memperoleh titik potong ini dapat dilakukan dengan menentukan nilai pengubah x apabila peubah y memiliki nilai sama dengan nol dalam fungsi kuadrat. Untuk itu titik potong yang diperoleh dapat berupa (x1, 0) dan (x2, 0), dimana akar persamaan kuadratnya berbentuk x1 dan x2. Akar akar dalam persamaan kuadrat ini disesuaikan dengan adanya diskriminan. Kita akan memperoleh satu akar saja apabila diskriminannya sama dengan nol. Maka dari itu dalam sumbu x hanya terdapat satu titik potong saja,
Apabila sumbu x tidak mempunyai titik potong, maka akar real tidak dimiliki oleh diskriminan yang nilainya kurang dari nol dalam persamaan kuadrat. Kemudian sumbu y dapat dicari titik potongnya dengan cara peubah x dalam fungsi kuadrat memiliki nilai yang sama dengan nol. Untuk itu titik yang diperoleh dapat berupa (0, y1).
Titik Ekstrim
Rangkuman materi fungsi kuadrat Matematika selanjutnya membahas tentang titik ekstrim. Pengertian titik ekstrim dalam fungsi kuadrat ialah koordinat yang memiliki nilai sumbu simetri (absis) dan nilai ekstrim (ordinat). Dalam fungsi kuadrat y = ax² + bx + c memiliki koordinat titik ekstrim sepasang dalam bentuk :

Keterangan :
D = Diskriminan, dengan rumus D = b² – 4ac
Sumbu dimetri = ![]()
Nilai ekstrim = ![]()
Baca juga : Materi Diagram Venn (Pengertian, Bentuk dan Contoh Soal)
Penjelasan di atas merupakan rumus titik ekstrim fungsi kuadrat yang diperoleh dalam pasangan koordinat titik ekstrim. Dalam rangkuman fungsi kuadrat Matematika tersebut juga saya jelaskan pembuktian rumus pada titik ekstrim. Pemerolehan titik ekstrim ini berasal dari dasar konsep turunan pertama. Untuk itu terlebih dahulu harus diturunkan sebelum memperoleh titik ekstrim fungsi kuadrat = ax² + bx + c. Setelah itu nilai y’ = 0 dimana turunannya memiliki hasil sama dengan nol. Maka dari itu bentuknya akan menjadi seperti di bawa ini:

Kemudian x pada titik ekstrim disubstitusikan ke dalam fungsi kuadrat awal sehingga dapat menjadi seperti di bawah ini:

Cara Menggambar Grafik Fungsi Kuadrat
Rangkuman materi fungsi kuadrat Matematika selanjutnya membahas tentang cara menggambar grafik fungsi kuadrat y = ax² + bx + c. Grafik fungsi kuadrat y = ax² + bx + c dapat digambar dengan beberapa langkah di bawah ini:
1. Menentukan titik potong pada sumbu koordinat. Adapun penjelasannya yaitu :
- Pada sumbu x terdapat titik potong apabila y = 0. Jika nilai D < 0 dimiliki oleh fungsi kuadrat, maka titik potong ini tidak dimiliki.
- Pada sumbu y terdapat titik potong apabila x = 0.
2. Langkah berikutnya ialah menentukan titik ekstrimnya dengan rumus:
Contoh Soal Fungsi Kuadrat
Dalam rangkuman fungsi kuadrat selanjutnya menjelaskan tentang contoh soal materi fungsi kuadrat. Fungsi kuadrat yang akan kita bedah berupa x² – 7x + 6. Dari fungsi kuadrat tersebut, kita dapat menentukan titik potong pada sumbu x maupun sumbu y. Adapun caranya yaitu sebagai berikut:
Baca juga : Cara Mencari Invers Matriks Ordo 2×2 dan 3×3 Lengkap
Titik Potong pada Sumbu X
Apabila y = 0, maka dapat memperoleh titik potong pada sumbu x, sehingga bentuk persamaan yang diperoleh dapat berupa x² – 7x + 6 = 0. Persamaan kuadrat ini dapat dipastikan mempunyai akar dengan cara menentukan diskriminan seperti di bawah ini:
D = b² – 4ac = (-7)² – 4(1)(6) = 49 – 24 = 25
Rumus diskriminan tersebut telah saya jelaskan dalam rangkuman materi fungsi kuadrat Matematika di atas. Dalam persamaan kuadrat tersebut nilai diskriminan yang dimiliki adalah 25 (positif) sehingga di dalamnya terdapat dua akar real berbeda. Dengan kata lain pada sumbu x terdapat dua titik potong yang dimiliki oleh fungsi kuadrat. Adapun akar akar persamaan kuadrat yang memperoleh titik potong sumbu x seperti di bawah ini:
x² – 7x + 6 = 0
(x – 1)(x – 6) = 0
x = 1 atau x = 6
Jadi pada sumbu x terdapat titik potong berupa (1,0) dan (6,0).
Titik Potong pada Sumbu Y
Apabila nilai x = 0, maka akan memperoleh titik potong pada sumbu y seperti di bawah ini:
y = x² – 7x + 6
= 0² – 7(0) + 6
= 6
Jadi titik potong dengan sumbu y ialah (0,6)
Titik Ekstrim
Dalam contoh soal fungsi kuadrat Matematika selanjutnya ialah menentukan titik ekstrim. Penjelasan titik ekstrim tersebut sudah saya jelaskan dalam rangkuman fungsi kuadrat Matematika di atas. Dalam materi fungsi kuadrat Matematika f(x) = ax² + bx + c terdapat titik ekstrim seperti di bawah ini:

Untuk itu titik ekstrim dalam fungsi ksuadrat f(x) = x² – 7x + 6 akan seperti di bawah ini:
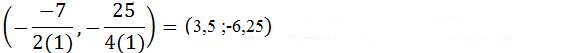
Dari sini terlihat 3,5 merupakan sumbu simetri dan -6,25 merupakan titik ekstrim. Setelah titik ekstrim, sumbu x dan sumbu y diketahui, langkah berikutnya ialah menggambar grafik fungsi kuadrat. Caranya yaitu membuat titik titik pada koordinat kartesius dan menghubungkannya pada kurva halus.
Cara menggambar grafik fungsi kuadrat ini telah saya jelaskan dalam rangkuman materi fungsi kuadrat Matematika di atas. Dalam contoh soal fungsi kuadrat f(x) = x² – 7x + 6 terdapat sumbu x yang titik potongnya (1,0) dan (6,0), sumbu y (0,6) dan titik ekstrim berupa (3,5; -6,25). Untuk itu gambarnya akan menjadi seperti di bawah ini:
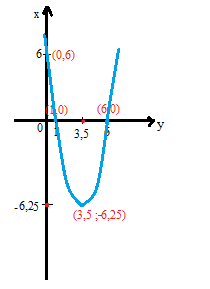
Demikianlah rangkuman materi fungsi kuadrat Matematika beserta contoh soal fungsi kuadrat. Pengertian fungsi kuadrat ialah suatu fungsi polinom yang mempunyai variabel atau peubah dengan pangkat paling tinggi berupa dua. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi fungsi kuadrat Matematika di atas.


