Materi Determinan Matriks (Pengertian, Rumus, dan Contoh Soal) – Menghafal rumus determinan matriks merupakan salah satu kewajiban peserta didik. Berkat pemahaman rumus serta konsep itu kita dapat menghitung serta menemukan jawaban dengan benar. Sayannya, tidak semua siswa mengetahui apa itu determinan matriks secara tepat.Padahal secara tidak langsung baik rumus ataupun sifat sifat determinan matriks ini selalu muncul dalam ujian dan tes. Matriks pada umumnya dapat dibagi menjadi beberapa macam tergantung besar ordonya. Untuk itu determinan matriksnya dapat berbentuk ordo 2 x 2, 3 x 3 ataupun n x n.
Tanpa perlu mencari, sebenarnya ada banyak sekali variasi contoh soal determinan matriks untuk bahan latihan. Determinan matriks paling sederhana dapat dicari pada matriks ordo 2 x 2. Determinan matriks 2×2 memang sering dijelaskan dalam pelajaran Sekolah Menengah Atas (SMA). Namun tidak menutup kemungkinan apabila determinan matriks ordo yang lebih besar juga dijelaskan. Misalnya saja determinan matriks 3 x 3 yang notabenya memiliki rumus dan cara menghitung yang lebih rumit.
Rumus determinan matriks merupakan satu dari sekian materi yang harus dipahami. Bukan sebuah rahasia lagi kalau banyak siswa kewalahan mengerjakan soal pada saat ulangan atau ujian. Inilah poin penting mengapa guru selalu memberikan latihan soal determinan matriks secara intensif. Selain menjabarkan pengertian, rumus, dan contoh soal, saya juga akan menjelaskan seperti apa sifat sifat determinan matriks sebagai tambahan referensi. Kalau kalian mengalami kesulitan memahami materi satu ini maka silahkan simak pembahasan sampai selesai.
Materi Determinan Matriks (Pengertian, Rumus, dan Contoh Soal)
Pengertian determinan matriks ialah suatu perhitungan nilai yang berasal dari unsur sebuah matriks persegi. Penulisan determinan matriks A dapat berupa det A, det (A) atau det |A|. Determinan dapat dinyatakan sebagai gambaran faktor penskalaan transformasi matriks. Cara menyelesaikan determinan matriks di setiap ordonya memiliki rumusnya masing masing.
Baca juga : Penaksiran Hasil Operasi Hitung Beserta Contoh Soalnya
Pada dasarnya konsep rumus determinan matriks setiap ordonya sama, baik ordo 2 x 2, 3 x 3 maupun n x n. Setelah memahami pengertian determinan matriks ini, kemudian saya akan membahas tentang rumus, sifat sifat determinan matriks dan contoh soal determinan matriks. Berikut penjelasan mengenai materi determinan matriks yaitu:
Determinan Matriks Ordo 2 x 2
Lambang nilai determinan A dapat berupa |A|. Determinan A ini dapat dihitung nilainya menggunakan rumus tertentu. Berikut rumus pada determinan matriks 2 x 2 yaitu:

Berdasarkan bentuk umum di atas kita dapat mengetahui rumus determinan matriks 2 x 2 yaitu sebagai berikut:
det (A) =|A|= ad – bc
Determinan Matriks Ordo 3 x 3
Materi determinan matriks selanjutnya ialah matriks ordo 3 x 3. Matriks ordo 3 x 3 ialah matriks yang memiliki baris dan kolom sebanyak tiga buah sehingga bentuknya menyerupai bujur sangkar. Matriks ini memiliki bentuk umum seperti berikut:
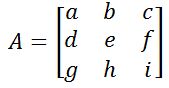
Gambar di atas merupakan bentuk matriks ordo 3 x 3. Jenis matriks ini dapat dicari nilai determinannya menggunakan rumus tertentu. Berikut rumus determinan matriks 3 x 3 yaitu:
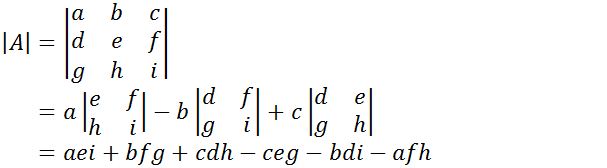
Baca juga : Rumus Bruto, Netto dan Tara Beserta Contoh Soal Lengkap
Determinan Matriks n x n
Materi determinan matriks selanjutnya membahas tentang determinan matriks pada ordo n x n. Determinan ini dapat dicari menggunakan rumus Leibniz seperti di bawah ini:
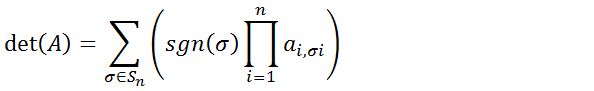
Rumus pada determinan matriks n x n di atas dapat diselesaikan dengan menggunakan metode eliminasi Gauss.
Sifat Sifat Determinan Matriks
Setelah menjelaskan tentang pengertian determinan matriks dan rumus determinan matriks di atas, baik ordo 2 x 2, 3 x 3, maupun n x n. Selanjutnya saya akan membahas tentang sifat sifat dalam cara menghitung determinan matriks. Penerapan sifat sifat ini biasanya digunakan untuk menyelesaikan contoh soal determinan matriks yang tersedia. Determinan matriks tersebut memiliki beberapa sifat seperti di bawah ini:
- Nilai determinan matriks akan nol jika semua elemen pada salah satu kolom atau baris bernilai sama dengan nol.
- Nilai determinan matriks akan nol jika semua elemen pada salah satu kolom atau baris sama dengan elemen kolom atau baris lainnya.
- Nilai determinan matriks akan nol jika elemen salah satu kolom atau barisnya ialah kelipatan elemen dari kolom atau baris lainnya.
- |AB| : |A| ×|B|
- |Aᵀ|=|A|, dimana Aᵀ merupakan transpose matriks A.
- |A‾¹|= 1/|A|, dimana A‾¹ merupakan invers matriks A.
- |kA|= kn|A|, dimana k ialah konstanta dan A memiliki ordo n x n.
Contoh Soal Determinan Matriks
Agar anda lebih paham mengenai materi determinan matriks terkait sifat sifat di atas. Selanjutnya saya akan membagikan contoh soal determinan matriks. Berikut contoh soal dan pembahasannya:
1. Diketahui matriks 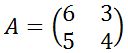 tersebut, tentukan determinan matriks A ini?
tersebut, tentukan determinan matriks A ini?
Jawab.
Untuk menyelesaikan soal tersebut, kita dapat menggunakan rumus determinan matriks ordo 2 x 2 seperti di bawah ini:
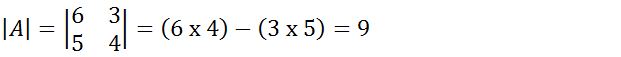
2. Diketahui matriks 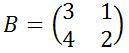 tersebut, tentukan determinan matriks B ini?
tersebut, tentukan determinan matriks B ini?
Jawab.
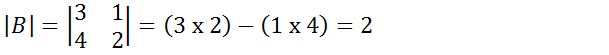
Demikianlah penjelasan mengenai materi determinan matriks, pengertian determinan matriks, rumus determinan matriks, sifat sifat determinan matriks dan contoh soal determinan matriks. Determinan matriks merupakan suatu perhitungan nilai yang berasal dari unsur sebuah matriks persegi. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.