Materi Fungsi Komposisi (Pengertian, Rumus, Sifat dan Contoh Soal) – Matematika menjadi salah satu mapel. Berbagai materi beserta rumus hitung yang cukup kompleks terkadang membuat siswa minder. Hal ini pun sering kita alami ketika mengerjakan soal ujian yang mana menuntut ketelitian, ketepatan, dan kecepatan. Menghitung fungsi komposisi menjadi salah satu hal yang harus kalian kuasai dalam pembelajaran.
Apa itu fungsi komposisi dan bagaimana cara menghitungnya? Sebenarnya rumus fungsi komposisi cukup mudah untuk dihafalkan jika kalian berpatokan pada sifat sifatnya. Materi ini sering disandingkan dengan materi fungsi invers. Untuk itu jika anda ingin mempelajari tentang fungsi komposisi, maka alangkah lebih baik jika anda memahami pula mengenai fungsi invers.
Dalam pembahasan mengenai materi fungsi komposisi tentunya terdapat beberapa hal yang dijelaskan. Hal hal tersebut mencakup pengertian fungsi komposisi, rumus fungsi komposisi, sifat sifat fungsi komposisi dan contoh soal fungsi komposisi. Fungsi komposisi merupakan operasi pada jenis fungsi f(x) yang digabungkan dengan fungsi g(x) hingga dapat menciptakan fungsi baru. Kita dapat menotasikan operasi fungsi komposisi menggunakan simbol atau huruf “o”. Pembacaan huruf atau simbol ini dapat berupa bundaran atau komposisi.
Materi Fungsi Komposisi (Pengertian, Rumus, Sifat dan Contoh Soal)
Tidak semua siswa menyukai mata pelajaran matematika ketika duduk di bangku sekolah menengah. Rumus hitung kompleks serta skill yang memerlukan ketelitian sering kali menjadi faktor utama rendahnya minat terhadap mapel ini.
Mempelajari rumus fungsi komposisi merupakan salah satu kewajiban kita sebagai siswa. Meski rumus fungsi tersebut tersaji di buku pedoman tapi faktanya masih banyak siswa kesulitan menghafalnya. Di lain sisi, ada pula yang mengeluh tak mampu mengerjakan contoh soal fungsi komposisi karena berbagai alasan klasik.
Seperti yang telah kita ketahui bahwa dalam fungsi komposisi terdapat dua fungsi yang digabungkan. Fungsi tersebut dapat berupa fungsi f(x) dan fungsi g(x). Lalu bagaimana operasi fungsi komposisi itu? Pada kesempatan kali ini saya akan menjelaskan tentang materi fungsi komposisi, pengertian fungsi komposisi, rumus fungsi komposisi, sifat sifat fungsi komposisi dan contoh soal fungsi komposisi.
Apa Itu Fungsi Komposisi
Fungsi komposisi dalam ilmu matematika adalah fungsi baru yang tercipta dari gabungan dua fungsi f(x) dan g(x). Terbentuknya fungsi baru dari f(x) dan g(x) tersebut dapat berupa:
- (f o g)(x) = g dimasukkan ke f
- (g o f)(x) = f dimasukkan ke g
Selain pengertian fungsi komposisi, adapula istilah mengenai fungsi tunggal. Apa yang dimaksud fungsi tunggal? Pengertian fungsi tunggal ialah suatu fungsi yang mempunyai lambang berupa huruf “f o g”. Lambang ini dapat dibaca dengan fungsi f bundaran g. Untuk menyelesaikan materi fungsi komposisi ini, kita dapat menghitung fungsi g terlebih dahulu. Setelah itu fungsi f nya baru dikerjakan.
Baca juga : Konversi Satuan Volume Dalam Kubik dan Liter
Berbeda lagi jika bentuk persamaan fungsi komposisinya “g o f” atau fungsi g bundaran f. Maka kita harus mengerjakan fungsi f terlebih dahulu, lalu fungsi g baru dikerjakan sehingga fungsi “g o f” dapat diselesaikan. Di bawah ini terdapat penjelasan mengenai rumus pada fungsi komposisi, sifat sifat fungsi komposisi dan contoh soal fungsi komposisi.
Rumus Fungsi Komposisi
Dalam materi fungsi komposisi tidak hanya memuat pengertian fungsi komposisi saja. Tapi kalian juga akan diajarkan bagaimana cara menghitung fungsi komposisi tersebut secara langsung. Sebab sedikit banyak materi ini akan muncul sebagai butir soal ujian baik itu PAS, PAT, maupun sekedar ulangan harian.
Inilah pentingnya kenapa kita harus menghafal rumus fungsi komposisi dengan benar. Karen sedikit saja kesalahan atau kurang teliti bisa menghasilkan jawaban salah. Seperti yang telah saya jelaskan di atas bahwa notasi operasi fungsi komposisi dapat berbentuk simbol atau huruf “o”. Berdasarkan terbentuknya fungsi baru di atas, kita dapat mengetahui rumus pada fungsi komposisi seperti di bawah ini:
y = f(x) jika f : A → B
y = g(x) jika g : B → A
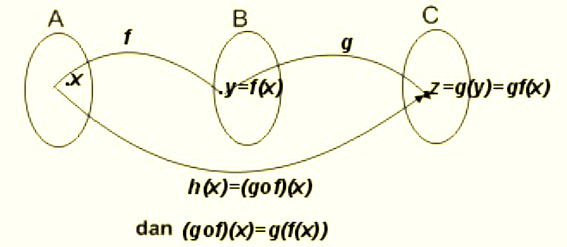
Dari rumus di atas,kita dapat memperoleh hasil fungsi g da f yang bentuknya:
h(x) = (g o f)(x) = g(f(x))
Jika diperjelas lagi, fungsi f dan fungsi g yang terlibat dengan fungsi komposisi dapat ditulis dalam bentuk seperti di bawah ini:
(g o f)(x) = g(f(x))
(f o g)(x) = f(g(x))
Baca juga : Latihan Soal Matematika Kelas 4 Semester 2 K13 dan Kunci Jawabannya
Sifat Sifat Fungsi Komposisi
Setelah menjelaskan tentang pengertian fungsi komposisi dan rumus fungsi komposisi di atas. Selanjutnya saya akan membahas tentang sifat sifat materi fungsi komposisi. Fungsi komposisi yang berbentuk f : A → B , g : B → C , h : C → D memiliki beberapa sifat di dalamnya yaitu:
- Tidak memberlakukan sifat komutatif sehingga (f o g)(x) ≠ (g o f)(x).
- Memiliki sifat asosiatif sehingga [f o (g o h)(x)] = [(f o g ) o h (x)].
- Memberlakukan (f o l)(x) = (l o f)(x) = f(x) pada fungsi identitasnya yaitu I (x).
Contoh Soal Fungsi Komposisi
Selain pengertian fungsi komposisi, rumus fungsi komposisi dan sifat sifat fungsi komposisi di atas. Adapula contoh soal materi fungsi komposisi terkait rumus yang digunakan. Berikut contoh soal dan pembahasannya yaitu:
Diketahui berturut turut f(x) dan g(x) terdapat fungsi f(x) = 4x + 3 dan g(x) = 3 – x. Maka tentukan nilai:
1. (f o g)(x)
2. (g o f)(x)
Pembahasan.
Contoh soal fungsi komposisi di atas dapat ditentukan dengan langkah langkah seperti di bawah ini:
f(x) = 4x + 3
g(x) = 3 – x
1. (f o g)(x)
Persamaan g(x) dimasukkan ke f(x), maka:
(f o g)(x) = f(g(x))
= f (3 – x)
= 4 (3 – x) + 3
= 12 – 4x + 3
= -4x + 15
2. (g o f)(x)
Persamaan f(x) dimasukkan ke g(x), maka:
(g o f)(x) = g(f(x))
= g (4x + 3)
= 3 – (4x + 3)
= 3 – 4x + 3
= -4x
Demikianlah penjelasan mengenai materi fungsi komposisi, pengertian fungsi komposisi, rumus fungsi komposisi, sifat sifat fungsi komposisi dan contoh soal fungsi komposisi. Fungsi komposisi merupakan fungsi baru yang berasal dari penggabungan dua fungsi yang berupa fungsi f(x) dan g(x). Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.


