Metode Penyelesaian Sistem Persamaan Linear Dua Variabel (SPLDV) Lengkap – Dalam pelajaran Matematika terdapat materi mengenai sistem persamaan linear. Persamaan linear tersebut masih dapat dibagi lagi menjadi beberapa macam tergantung banyaknya variabel di dalamnya. Contohnya persamaan linear satu variabel, persamaan linear dua variabel atau sering disingkat SPLDV dan sebagaiya. Apa itu SPLDV? Bagaimana menyelesaikan sistem persamaan ini?Apa saja metode SPLDV? Sistem Persamaan Linear Dua Variabel ialah persamaan linear yang mengandung dua variabel, dimana derajat atau kuadratnya sama dengan 1.
Seperti yang telah saya jelaskan di atas bahwa sistem persamaan linear dapat dibagi menjadi beberapa jenis. Masing masing jenisnya didasarkan sesuai dengan jumlah variabel di dalamnya. Meskipun jumlah variabelnya berbeda, tetapi cara menyelesaikan persamaan linearnya hampir sama atau tidak jauh berbeda dengan penyelesaian persamaan linear secara umum.

Sistem persamaan linear dalam Matematika pada dasarnya dapat berbentuk satu variabel maupun dua variabel. Namun paling sering orang orang kesulitan dalam menyelesaikan soal soal sistem persamaan linear dua variabel ini. Untuk itu agar soal soal SPLDV dapat anda kerjakan dengan mudah, maka anda perlu untuk mengetahui konsep dasar SPLDV dan metode penyelesaian sistem persamaan linear dua variabel terlebih dahulu.
Metode Penyelesaian Sistem Persamaan Linear Dua Variabel Lengkap
Ketika di bangku sekolah, materi persamaan linear dalam ilmu Matematika dianggap sulit oleh beberapa siswa. Hal ini dikarenakan persamaan tersebut mengandung variabel di dalamnya. Sebelum membahas tentang metode penyelesaian SPLDV tersebut. Saya akan menjelaskan terlebih dahulu mengenai pengertian SPLDV, ciri ciri dan hal hal yang berkaitan dengan SPLDV atau sistem persamaan linear dua variabel.
Baca juga : Rumus Perpangkatan Aljabar Beserta Contoh Soal
Apa yang dimaksud SPLDV? Pengertian SPLDV ialah bentuk persamaan yang mempunyai dua variabel dengan masing masing variabel memiliki pangkat satu. Selain itu persamaan ini akan membentuk garis lurus jika digambarkan dalam bentuk grafik. Dalam metode penyelesaian sistem persamaan linear dua variabel (SPLDV) terdapat ciri ciri khusus yang terkandung didalamnya. Berikut ciri ciri sistem persamaan linear dua variabel atau SPLDV:
- Memiliki tanda relasi sama dengan (=).
- Mempunyai dua variabel.
- Setiap variabel mempunyai pangkat satu.
Selain ciri ciri di atas, adapula hal hal yang berkaitan dengan metode penyelesaian SPLDV. Berikut beberapa hal yang dimaksud yaitu diantaranya:
Suku
Suku merupakan bagian dari aljabar yang tersusun oleh variabel, konstanta dan koefisien. Masing masing suku tersebut terpisah oleh tanda baca pengurangan ataupun penjumlahan. Misalnya:
2x – 3y + 6
Persamaan di atas memiliki suku suku yaitu 2x, -3y dan 6.
Variabel
Metode penyelesaian sistem persamaan linear dua variabel (SPLDV) selanjutnya berkaitan dengan variabel. Variabel ialah bilangan yang diganti dengan simbol huruf, seperti x dan y. Misalnya:
Andi mempunyai 4 buku tulis dan 3 bolpoint. Apabila digambarkan dalam bentuk persamaan maka akan menjadi 4x + 3y, dimana x = buku tulis dan y = bolpoint.
Koefisien
Metode penyelesaian SPLDV selanjutnya berkaitan dengan koefisien. Koefisien ialah bilangan yang dapat menegaskan jumlah variabel yang sama. Koefisien biasanya terdapat didepan variabel. Misalnya:
Andi mempunyai 4 buku tulis dan 3 bolpoint. Apabila digambarkan dalam bentuk persamaan maka akan menjadi 4x + 3y, dimana x = buku tulis dan y = bolpoint. Angka 4 merupakan koefisien dari x dan angka 3 merupakan koefisien dari y.
Konstanta
Konstanta ialah bilangan yang tidak disertai variabel. Dengan kata lain nilainya konstan atau tetap tanpa perubahan nilai. Misalnya:
2x – 3y + 6
Persamaan di atas memiliki konstanta 6. Hal ini dikarenakan 6 bernilai tetap dan tidak berubah sebab tidak terpengaruh oleh variabel.
Baca juga : Operasi Hitung Pecahan Aljabar Beserta Contoh Soal Lengkap
Untuk menggunakan metode penyelesaian sistem persamaan linear dua variabel (SPLDV) tersebut, biasanya terdapat beberapa syarat khusus yang harus dipenuhi. Adapun syarat penyelesesaian SPLDV yaitu
- Terdapat dua persamaan linear dua variabel yang sama.
- Kedua jenis persamaan linear dua variabel harus membentuk sistem persamaan linear dua variabel (SPLDV).
Metode Penyelesaian Sistem Persamaan Linear Dua Variabel
Metode penyelesaian SPLDV dapat dibagi menjadi beberapa cara yaitu menggunakan metode substitusi, eliminasi dan campuran. Setiap cara memiliki langkahnya sendiri sendiri. Berikut penjelasannya:
Metode Substitusi (Mengganti)
Metode substitusi ialah metode penyelesaian SPLDV dengan cara mengganti salah satu variabelnya. Untuk lebih jelasnya dapat anda simak contoh soal SPLDV di bawah ini:
Contoh Soal
1. Hitunglah himpunan penyelesaian dari persamaan x + 2y = 12 dan 2x + 8y = 20!
Jawab.
Cara pertama:
x + 2y = 12
<> x = -2y + 12 . . . (Persamaan 1)
2x + 8y = 20 . . . (Persamaan 2)
Setelah itu carilah nilai y dengan memasukkan persamaan 1 ke persamaan 2. Maka akan menjadi:
2x + 8y = 20
<> 2 (-2y + 12) + 8y = 20
<> -4y +24 + 8y = 20
<> 4y = 20 – 24
<> 4y = -4
<> y = -4/4 = -1
Nilai y tadi dapat disubstitusikan ke persamaan 1 ataupun persamaan 2.
x = -2y + 12
= -2(-1) + 12
= 2 + 12
= 14
Jadi Himpunan Penyelesainnya = {14 , -1}
2. Tentukan nilai x dan y pada bersamaan 2x + 6y = 22 dan 3x + y = 9!
Jawab.
Contoh soal sistem persamaan linear dua variabel ini dapat diselesaikan dengan cara cara seperti berikut:
Cara pertama:
2x + 6y = 22 . . . (Persamaan 1)
3x + y = 9
<> y = -3x + 9 . . . (Persamaan 2)
Setelah itu carilah nilai y dengan memasukkan persamaan 2 ke persamaan 1. Maka akan menjadi:
2x + 6y = 22
<> 2x + 6(-3x + 9) = 22
<> 2x -18x + 54 = 22
<> -16x + 54 = 22
<> -16x = 22 – 54
<> x = -32/-16 = 2
Nilai x tadi dapat disubstitusikan ke persamaan 1 ataupun persamaan 2.
y = -3x + 9
= -3(2) + 9
= -6 + 9
= 3
Jadi nilai x dan y adalah 2 dan 3.
Metode Eliminasi (Menghilangkan)
Metode penyelesaian sistem persamaan linear dua variabel (SPLDV) selanjutnya menggunakan cara eliminasi atau menghilangkan. Metode eliminasi ialah metode penyelesaian SPLDV dengan cara menghilangkan salah satu variabelnya dan menyamakan koefisien disetiap persamaannya.
Untuk metode penyelesaian SPLDV ini harus memperhatikan tanda yang terletak didepan koefisiennya. Jika tandanya sama sama (+) atau (-) maka menjadi operasi penjumlahan. Tetapi jika tandanya (+) dan (-) maka menjadi operasi pengurangan.
Contoh Soal
1. Hitunglah himpunan penyelesaian dari persamaan x + 2y = 12 dan 2x + 8y = 20!
Baca juga : 6 Macam Pola Bilangan Matematika Beserta Rumusnya
Jawab.
Contoh soal sistem persamaan linear dua variabel ini dapat diselesaikan dengan cara seperti berikut:
Cara pertama ialah menentukan variabel manakah yang akan dihilangkan. Anda dapat menghilangkan variabel x terlebih dahulu ataupun sebaliknya.
x + 2y = 12 . . . (Persamaan 1)
2x + 8y = 20 . . . (Persamaan 2)
Eliminasi persamaan 1 dan persamaan 2, maka menjadi:
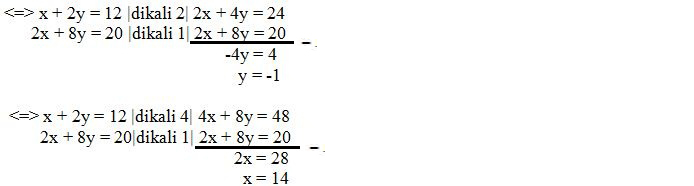
Jadi Himpunan Penyelesaian = {14, -1}
2. Tentukan nilai x dan y pada bersamaan 2x + 6y = 22 dan 3x + y = 9!
Jawab.
Contoh soal SPLDV ini dapat diselesaikan dengan cara seperti berikut:
Cara pertama ialah menentukan variabel manakah yang akan dihilangkan. Anda dapat menghilangkan variabel x terlebih dahulu ataupun sebaliknya.
2x + 6y = 22 . . . (Persamaan 1)
3x + y = 9 . . . (Persamaan 2)
Eliminasi persamaan 1 dan persamaan 2, maka menjadi:
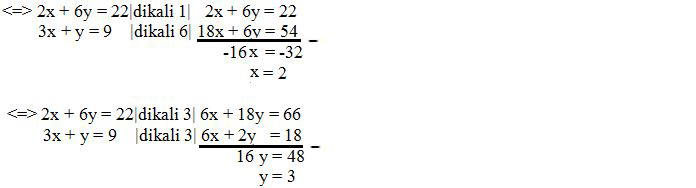
Jadi nilai x dan y adalah 2 dan 3.
Metode Campuran (Substitusi dan Eliminasi)
Metode penyelesaian sistem persamaan linear dua variabel (SPLDV) yang terakhir menggunakan cara substitusi dan eliminasi (campuran). Metode campuran ialah metode penyelesaian SPLDV yang menggabungkan metode subtitusi dengan eliminasi.
Contoh Soal
Hitunglah himpunan penyelesaian dari persamaan x + 2y = 12 dan 2x + 8y = 20!
Contoh soal SPLDV ini dapat diselesaikan dengan cara seperti berikut:
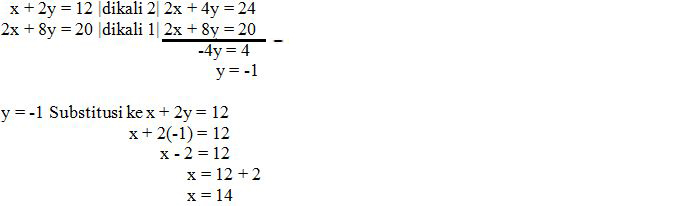
Jadi Himpunan Penyelesaian = {14, -1}
Demikianlah penjelasan mengenai metode penyelesaian sistem persamaan linear dua variabel (SPLDV) lengkap. Untuk metode penyelesaian SPLDV dapat menggunakan tiga cara yaitu substitusi, eliminasi dan campuran. Namun lebih efektif menggunakan metode campuran karena caranya lebih efisien dan cepat. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi SPLDV di atas.


