Cara Menentukan Faktor Prima Suatu Bilangan Beserta Contoh Soal – Faktorisasi prima adalah materi dasar matematika yang harusnya sudah diajarkan pada siswa bahkan semenjak masih berada di bangku SD. Ketika jenjang SMP maupun SMA pendalaman materi pun dilakukan karena menghitung faktor suatu bilangan menjadi salah satu materi pokok dalam pembelajaran K13. Rumus faktor prima bilangan pun menurut saya sangat mudah untuk dipelajari karena memiliki pola tertentu.
Tapi sebenarnya apa itu faktor prima pada bilangan? Bagaimana cara menyelesaikan contoh soal faktor prima? Faktor prima memiliki konsep yang berbeda dengan faktorisasi prima dan bilangan prima. Akan tetapi untuk memahami tentang materi faktor prima ini, alangkah lebih baik jika anda mengetahui tentang materi bilangan prima terlebih dahulu. Apa yang dimaksud dengan bilangan prima itu? Bilangan prima ialah bilangan yang mempunyai dua faktor pembagi saja seperti bilangan itu sendiri dan bilangan satu. Adapun contoh bilangan prima yaitu angka 2, 3, 5, 7, 11, 13 dan sebagainya.
Untuk mengidentifikasi bilangan prima memang cukup mudah untuk dipahami karena bilangannya hanya dapat dibagi habis dengan angka satu dan bilangan itu sendiri. Misalnya angka 7 yang hanya dapat dibagi habis dengan angka 7 dan 1, angka 13 dibagi habis dengan angka 13 dan 1, serta yang lainnya. Berbeda lagi dengan bilangan 8 yang dapat dibagi dengan 1, 2, 4 dan 8. Untuk itulah angka 8 tidak termasuk dalam bilangan prima karena unsur pembaginya lebih dari 2. Bilangan prima ini dapat mendukung cara menentukan faktor prima suatu bilangan. Maka dari itu contoh soal faktor prima ini dapat anda selesaikan dengan mudah.
Cara Menentukan Faktor Prima Suatu Bilangan Beserta Contoh Soal
Cara mencari faktor prima bilangan bisa kalian lakukan tanpa repot menghitung menggunakan rumus yang rumit. Dengan membagi bilangan tersebut secara berulang menggunakan bilangan prima sampai bilangan itu tidak bisa dibagi lagi. Dari penjelasan ini kita dapat melihat peran bilangan prima dalam pola hitungnya. Bilangan tersebut digunakan untuk membagi bilangan yang difaktorkan.
Sering kali materi faktor prima pada bilangan diajarkan diajarkan secara intensif pada murid SMP dan SMA. Meski pola serta rumus hitung tidak terlalu sulit tapi tidak serta merta kita bisa melihatnya sebelah mata. Faktanya, masih banyak siswa terkecoh ketika mengerjakan soal faktor prima bilangan tertentu pada ulangan harian maupun ujian.
Berdasarkan problematika di atas akhirnya saya tergelitik ingin membahas lebih dalam materi faktorisasi prima. Pada artikel ini kita akan belajar bagaimana cara menentukan faktor prima suatu bilangan. Metode paling cepat untuk menguasai materi adalah dengan mengerjakan langsung contoh soal faktor prima itu sendiri. Setidaknya melalui artikel berikut kalian dapat mendalami materi serta mempraktekan latihan soal untuk menghadapi ujian mendatang.
Rumus Faktor Prima
Sebenarnya materi faktorisasi prima memang sudah mulai diberikan pada siswa bahkan sejak dini. Meski guru memberikan berbagai model pembekalan sayangnya masih ada sebagian siswa kurang memahami materi. Hal ini pun menurut saya cukup lumrah karena masing-masing orang memiliki tingkat intelijensi berbeda untuk menghafal rumus cepat.
Seperti yang telah kita ketahui bahwa faktor prima suatu bilangan dapat kita tentukan dengan mudah. Adapun caranya yaitu bilangan tersebut dibagi secara berulang ulang dengan bilangan prima terkecil sampai pembagiannya tidak bisa dilakukan lagi dengan bilangan prima tadi. Untuk itulah anda harus memahami terlebih dahulu mengenai materi bilangan prima.
Baca juga : Rumus Lingkaran Dalam Segitiga dan Lingkaran Luar Segitiga
Dari sini kita tahu bahwa cara menentukan faktor prima suatu bilangan ini memang cukup dengan operasi hitung pembagian saja. Agar anda lebih paham mengenai materi faktor prima ini, maka perhatikan contoh soal faktor prima dari bilangan 360. Untuk menyelesaikan faktor bilangan tersebut dapat dilakukan dengan menggunakan pohon faktor seperti di bawah ini:
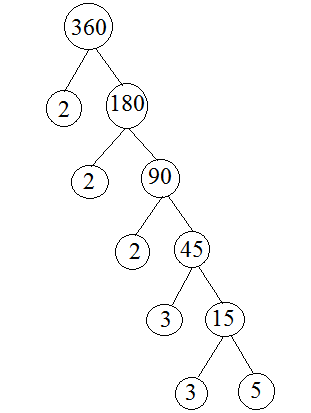
Berdasarkan pohon faktor di atas, kita dapat menemukan faktorisasi prima bilangan 360 yaitu 2 x 2 x 2 x 3 x 3 x 5. Untuk itu faktor primanya ialah 2, 3 dan 5. Cara membuat pohon faktor tersebut dapat dilakukan dengan membagi bilangannya menggunakan bilangan prima terkecil sampai tidak dapat di bagi lagi. Penggunaan bilangan bilangan ini menyesuaikan bilangan yang difaktor primakan.
Contoh Soal Faktor Prima
Setelah menjelaskan tentang cara menentukan faktor prima suatu bilangan di atas, selanjutnya saya akan membagikan contoh soal terkait materi faktor prima tersebut. Berikut contoh soal dan pembahasannya:
1. Tentukan faktor prima 56?
Baca juga : Contoh Soal Barisan dan Deret Geometri SMA/SMK Beserta Pembahasan
Pembahasan.
Contoh soal faktor prima ini dapat diselesaikan dengan cara seperti berikut:
- 56 dibagi dengan 2 (bilangan prima terkecil) sehingga menjadi 56 : 2 = 28.
- 28 dibagi dengan 2 (bilangan prima terkecil) sehingga menjadi 28 : 2 = 14.
- 14 dibagi dengan 2 (bilangan prima terkecil) sehingga menjadi 14 : 2 = 7.
- Hasil akhirnya ialah bilangan 7 yang tidak dapat dibagi dengan bilangan prima lagi.
Dari penjelasan di atas di peroleh faktorisasi prima dari 56 ialah 2 x 2 x 2 x 7.
Jadi faktor prima dari 56 ialah 2 dan 7.
2. Tentukan faktor prima dari 64?
Pembahasan.
Cara menentukan faktor prima ini dapat dilakukan dengan menggunakan pohon faktor juga. Untuk itu hasilnya akan menjadi seperti berikut:
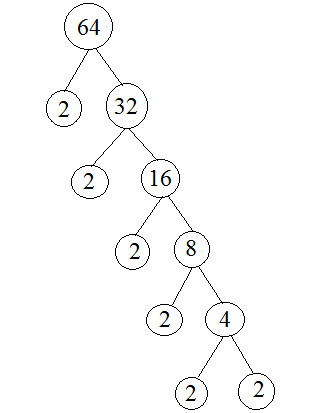
Keterangan pohon faktor di atas yaitu:
- 64 dibagi dengan 2 (bilangan prima terkecil) sehingga menjadi 64 : 2 = 32.
- 32 dibagi dengan 2 (bilangan prima terkecil) sehingga menjadi 32 : 2 = 16.
- 16 dibagi dengan 2 (bilangan prima terkecil) sehingga menjadi 16 : 2 = 8.
- 8 dibagi dengan 2 (bilangan prima terkecil) sehingga menjadi 8 : 2 = 4.
- 4 dibagi dengan 2 (bilangan prima terkecil) sehingga menjadi 4 : 2 = 2
- Hasil akhirnya ialah bilangan 2 yang tidak dapat dibagi dengan bilangan prima lagi.
Dari penjelasan di atas di peroleh faktorisasi prima dari 64 ialah 2 x 2 x 2 x 2 x 2 x 2.
Jadi faktor prima dari 64 ialah 2.
Sekian penjelasan mengenai cara menentukan faktor prima suatu bilangan beserta contoh soal faktor prima. Faktor prima dapat ditentukan dengan menggunakan pohon faktor, dimana bilangannya dibagi dengan bilangan prima secara terus menerus. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi faktor prima di atas.