Rumus Deret Geometri Tak Hingga Beserta Contoh Soal – Dalam Matematika terdapat materi deret geometri tak hingga yang tidak kalah penting untuk dipelajari. Apa pengertian deret geometri tak hingga itu? Bagaimana cara menyelesaikan contoh soal deret geometri tak hingga? Deret geometri tak hingga memiliki bentuk umum tertentu. Bentuk umum deret geometri tak hingga dapat berupa a + ar + ar² + ar³ + (…) seterusnya.
Pada rumus deret geometri tak hingga di atas r ialah rasio dan a suku pertama. Kemudian adapula tanda titik tiga (…) yang menjelaskan tentang penjumlahan dengan pola deret yang sama pada bagian berikutnya secara terus menerus. Geometri deret tak hingga pada umumnya dapat dibagi menjadi dua jenis. Apa saja jenis jenis deret geometri tak hingga itu? Macam macam deret geometri tak hingga tersebut dapat berupa divergen maupun konvergen.
Jenis jenis deret geometri tak hingga ini pada dasarnya memiliki rumus deret geometri tak hingga yang hampir sama. Selain itu cara menyelesaikan contoh soal deret geometri tak hingga dari kedua jenis tadi juga serupa. Konvergen dapat diartikan sebagai menuju atau memusat pada sebuah titik tertentu. Sedangkan divergen dapat diartikan menyebar, tidak memusat, mungkin konstan atau berisolalsi dan tidak menuju pada sebuah titik tertentu.
Untuk melihat kekonvergenan deret geometri dapat berasal dari rasio deret tersebut. Oleh karenanya apabila jumlah jika dan hanya jika |r|< 1, maka deret geometri tak hingga dapat dinyatakan konvergen. Kemudian apabila tidak memiliki jumlah serta nilainya jika dan hanya jika |r|≥ 1, maka deret geometri tak hingga dapat dinyatakan divergen.
Rumus Deret Geometri Tak Hingga Beserta Contoh Soal
Materi deret geometri tak hingga dapat diamati pada penjatuhan bola bekel setinggi 60 cm dari atas meja. Setelah itu akan terjadi pemantulan bola bekel hingga akhirnya dapat berhenti. Bola akan melakukan pantulan pertama yang lebih tinggi dibandingkan pantulan kedua. Hal ini juga berlaku untuk ketinggian pantulan kedua daripada pantulan ketiga dan seterusnya.
Dalam proses pemantilan tersebut tinggi setelahnya memiliki besar ½ dari tinggi pada pantulan sebelumnya. Pemantulan tersebut akan terus ada sampai bola dapat berhenti. Inilah konsep dari deret geometri tak hingga. Pada kesempatan kali ini saya akan menjelaskan tentang rumus deret geometri tak hingga beserta contoh soal deret geometri tak hingga. Untuk lebih jelasnya dapat anda simak di bawah ini.
Apa Itu Deret Geometri Tak Hingga
Pengertian deret geometri tak hingga adalah suku suku yang dijumlahkan begitu banyaknya. Penjumlahan itu bahkan mencapai angka tak terhingga atau tidak terbatas pada barisan geometri. Deret geometri tak terhingga ini dapat dilambangkan dengan notasi “S∞”.
Rumus deret geometri tak hingga tidak terlalu sulit untuk kita hafalkan. Sebab masih berhubungan dengan jumlah suku tertentu meski jumlahnya banyak dant ak Suku suku yang dijumlahkan ini tentunya memiliki banyak yang tidak terbatas. Maka deret geometri tak terhingga secara matematis dapat dibentuk seperti di bawah ini:
S∞ = U₁ + U₂ + U₃ + …
Pada umumnya persamaan di atas merupakan rumus deret geometri tak hingga secara umum. Rumus geometri tak terhingga ini dapat dijadikan dasar dalam mengerjakan contoh soal deret geometri tak hingga tersebut. Seperti yang telah saya jelaskan di atas bahwa deret ini dapat dibagi menjadi beberapa jenis. Berikut macam macam deret geometri tak hingga yaitu:
Baca juga : Rumus Koefisien Variasi Beserta Pengertian dan Contoh Soal
Jenis Jenis Deret Geometri Tak Hingga
Sebelum belajar rumus deret geometri tak hingga kalian harus memahami terlebih dulu jenisnya. secara umum ada deret geometri tak hingga divergen dan deret geometri tak hingga konvergen. Setiap jenis deret geometri tak terhingga memiliki penjelasan dan rumus yang berbeda beda.
Deret Geometri Tak Hingga Konvergen
Konvergen dapat diartikan sebagai tidak menyebar atau memusat. Untuk itu pengertian deret geometri tak hingga konvergen ialah deret geometri yang mempunyai jumlah limit tertentu. Deret tak hingga ini memiliki syarat khusus berupa letak rasiao diantara 1 dengan -1 sehingga nilainya |r|< 1 atau -1 < r < 1. Di bawah ini terdapat rumus deret geometri tak hingga konvergen yaitu diantaranya:
Deret Geometri Tak Hingga Divergen
Jenis jenis deret geometri tak hingga selanjutnya ialah divergen. Divergen dapat diartikan sebagai menyebar. Untuk itu deret geometri ini memiliki jumlah yang tidak terbatas. Untuk itu deret geometri tak terhingga divergen memiliki syarat berupa r > 1 atau r < -1. Di bawah ini terdapat rumus deret geometri tak terhingga yaitu diantaranya:
Contoh Soal Deret Geometri Tak Hingga
Setelah menjelaskan tentang pengertian deret geometri tak hingga dan rumus deret geometri tak hingga tersebut. Selanjutnya saya akan membagikan contoh soal terkait materi deret geometri tak hingga ini. Berikut contoh soal deret geometri tak terhingga yaitu meliputi:
1. Perhatikan gambar di bawah ini!
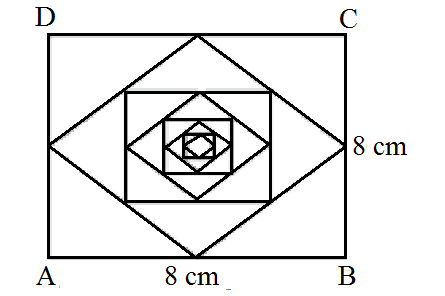 Seperti yang telah anda lihat di atas bahwa persegi persegi lainnya terdapat dalam persegi ABCD secara terus menerus. Pengambilan 4 titik sudut persegi itu berasal dari titik tengah persegi sebelumnya. Hitunglah jumlah luas persegi yang dibentuk?
Seperti yang telah anda lihat di atas bahwa persegi persegi lainnya terdapat dalam persegi ABCD secara terus menerus. Pengambilan 4 titik sudut persegi itu berasal dari titik tengah persegi sebelumnya. Hitunglah jumlah luas persegi yang dibentuk?
Baca juga : Cara Perkalian Bersusun Panjang dan Pendek Beserta Contoh
Pembahasan.
Contoh soal deret geometri tak hingga tersebut dapat disesaikan dengan menggunakan konsep rumus deret geometri tak terhingga di atas. Di bawah ini terdapat gambar persegi kedua dan pertama seperti berikut:
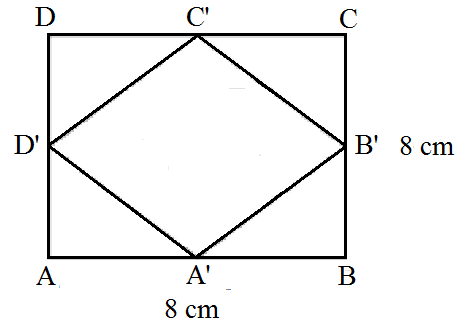
Luas total persegi dinyatakan dalam huruf L. Untuk itu rumus L secara matematis akan menjadi seperti di bawah ini:
L = Lᴀᴃᴄᴅ + Lᴀ‘ᴃ‘ᴄ‘ᴅ‘
Maka dari itu nilai Lᴀ‘ᴃ‘ᴄ‘ᴅ‘ = ½ Lᴀᴃᴄᴅ, dimana persamaan ini berlaku untuk persegi persegi berikutnya. Untuk itu besar luasnya 0,5 kali luas persegi sebelumnya. Berdasarkan rumus deret geometri tak hingga tersebut, maka dapat kita peroleh hasil perhitungan seperti berikut:
Luas persegi total : Lᴀᴃᴄᴅ = 8 x 8 = 64 cm²
L = 64 + 32 + 16 + …
a = 64, r = ½
Sehingga. Jadi jumlah luas persegi yang dibentuk ialah 120 cm².
Jadi jumlah luas persegi yang dibentuk ialah 120 cm².
2. Diketahui jumlah deret geometri tak hingganya ialah empat kali suku pertamanya. Maka tentukan rasio dari deret tersebut?
Pembahasan.
Diketahui : S∞ = 4a
Ditantakan : r = ?
Jawab.
Contoh soal deret geometri tak hingga dapat diselesaikan menggunakan rumus deret geometri tak hingga seperti di bawah ini:
S∞ = a / 1-r
4a = a / 1-r
1 – r = a / 4a
1 – r = ¼
-r = ¼ – 1
-r = -¾
r = ¾
Jadi rasio deret geometri tak hingga tersebut ialah ¾.
Demikianlah penjelasan mengenai rumus deret geometri tak hingga beserta contoh soal deret geometri tak hingga. Pengertian deret geometri tak hingga ialah suku suku yang dijumlahkan dengan banyak tak terhingga atau tidak terbatas pada barisan geometri. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi deret geometri tak hingga di atas.