Materi Teorema Sisa dan Teorema Faktor Beserta Contoh Soal – Dalam ilmu Matematika kelas 11 SMA terdapat materi pembelajaran mengenai suku banyak (Polinomial). Dalam materi polinomial terdapat pembahasan tentang materi teorema faktor dan teorema sisa. Di dalamnya terdapat penjelasan lengkap mengenai rumus teorema sisa, rumus teorema faktor, cara mengerjakan contoh soal teorema sisa dan cara mengerjakan contoh soal teorema faktor. Materi dalam teorema sisa dan faktor tersebut masih berkaitan dengan materi pembagian polinomial (suku banyak). Dalam pembagian polinomial ini terdapat cara untuk mengetahui sisa hasil bagi maupun hasil bagi dari suku banyak tersebut.

Materi teorema sisa dan teorema faktor memang berhubungan dengan suku banyak atau polinomial. Teorema sisa tersebut digunakan untuk mengetahui secara langsung sisa hasil bagi tanpa harus melalui proses pembagian. Penggunaan teorema sisa tersebut memang untuk mencari sisa hasil bagi yang terdapat di dalam suku banyak. Kemudian adapula materi teorema faktor yang berguna dalam suku banyak untuk mengetahui faktor faktornya. Kita dapat menggunakan teorema sisa untuk menghitung sisa hasil pembagian suku banyak yang jumlahnya nol atau tidak memiliki sisa, maka hal ini termasuk dalam faktor sebuah bilangan.
Seperti yang telah kita tahu bahwa materi suku banyak (Polinomial) memiliki rumus atau bentuk umumnya sendiri. Untuk itu dalam teorema sisa dan materi teorema faktor tersebut juga memiliki rumusnya masing masing. Rumus teorema sisa dan rumus teorema faktor ini digunakan untuk menghitung contoh soal teorema sisa dan contoh soal teorema faktor. Nah pada kesempatan kali ini saya akan menjelaskan tentang materi teorema sisa dan teorema faktor beserta contoh soal. Untuk lebih jelasnya dapat anda simak di bawah ini.
Materi Teorema Sisa dan Teorema Faktor Beserta Contoh Soal
Sebelum menjelaskan tentang materi terkait teorema sisa, materi teorema faktor, rumus teorema sisa, rumus teorema faktor, contoh soal teorema sisa dan contoh soal teorema faktor tersebut. Saya akan menjelaskan sedikit mengenai materi suku banyak atau polinomial terlebih dahulu. Pengertian polinomial ialah sebuah suku suku yang dibentuk karena banyak nilainya sehingga penyusunannya berdasarkan perubah konstanta dan variabel. Operasi yang digunakan dapat berupa pengurangan, pangkat bilangan bulat tidak negatif, penjumlahan dan perkalian.
Baca juga : Cara Menghitung Frekuensi Harapan Beserta Rumus dan Contoh Soal
Suku banyak atau Polinomial memiliki bentuk umum dengan variabel x dan berderajat n. Maka bentuk umum suku banyak atau polinomialnya akan menjadi ![]() . Dalam hal ini
. Dalam hal ini ![]() merupakan konstanta atau koefisien polinom dan an ≠ 0 serta n = bilangan bulat yang positif. x memiliki pangkat paling tinggi yang berupa derajat polinomial, serta mengandung suku konstan (tetap) sebagai suku yang tidak mempunyai variable (a).
merupakan konstanta atau koefisien polinom dan an ≠ 0 serta n = bilangan bulat yang positif. x memiliki pangkat paling tinggi yang berupa derajat polinomial, serta mengandung suku konstan (tetap) sebagai suku yang tidak mempunyai variable (a).
Mempelajari rumus teorema faktor dan sisa menurut saya sangatlah penting untuk menambah wawasan. Pemahaman tersebut benar-benar bisa menolong kita saat berhadapan langsung dengan soal latihan ataupun ulangan. Maka dari itu, apabila berkenan simaklah artikel yang sedikit banyak akan membahas materi teorema di bawah.
Teorema Sisa
Ketika menguasai rumus teorema sisa maka kalian tak perlu lagi melakukan pembagian secara kompleks untuk mengetahui berapa sisa hitungan. Faktanya, materi teorema sisa menjadi salah satu pokok bahasan penting yang wajib kalian kuasai di jenjang sekolah menengah. Maka dari itu, selain mengajarkan rumusnya, saya juga akan memberikan contoh soal teorema sisa sebagai latihan.
Rumus Teorema Sisa
Hal pertama yang akan saya bahas dalam materi suku banyak (polinomial) ini adalah teorema sisa. Dalam pembagian suku banyak tersebut terdapat bentuk umum yang berupa persamaan seperti di bawah ini:
f (x) = p (x) . H (x) + S (x)
Keterangan :
f(x) = Suku banyak
p(x) = Pembagi suku banyak
H(x) = Hasil bagi suku banyak
S(x) = Sisa suku banyak
Berdasarkan rumus di atas dapat diketahui beberapa hal yang penting dalam materi teorema sisa tersebut. Teorema sisa ini memiliki beberapa hal penting seperti di bawah ini:
- Apabila n merupakan derajat dari suku banyak f(x), maka dapat dibagi dengan (x – k) sehingga ditemukan S(x) = f(x) sebagai sisanya.
- Apabila n merupakan derajat dari suku banyak f(x), maka dapat dibagi dengan (ax + b) sehingga ditemukan S(x) = f(-a/b) sebagai sisanya.
- Apabila n merupakan derajat dari suku banyak f(x), maka dapat dibagi dengan (x – a)(x – b) sehingga ditemukan
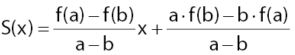 sebagai sisanya.
sebagai sisanya.
Baca juga : Latihan Soal UN Matematika SD 2020 dan Kunci Jawabannya Terlengkap
Agar anda lebih memahami tentang teorema sisa ini, maka saya akan membagikan contoh soal teorema sisanya. Adapun contoh soal dan pembahasannya yaitu sebagai berikut:
Contoh Soal Teorema Sisa
Hitunglah sisa hasil bagi antara f(x) = x² + 2x + 4 dengan x + 1!
Jawab.
Untuk menghitung sisa hasil bagi dalam soal di atas, kita dapat menerapkan persamaan teorema sisa yang pertama yaitu “apabila n merupakan derajat dari suku banyak f(x), maka dapat dibagi dengan (x – k) sehingga ditemukan S(x) = f(x) sebagai sisanya”.
Maka dari itu dapat diperoleh nilai k yang disubstitusikan menuju persamaan suku banyak. Sehingga hasilnya:
x + 1 → k = -1
nilai k = -1 dapat disubstitusikan ke persamaan f(x) = x² + 2x + 4. Maka hasilnya:
f(x) = x² + 2x + 4
f(-1) = (-1)² + 2(-1) + 4
f(-1) = 1 – 2 + 4
f(-1) = 3
Jadi sisa hasil pembagian dalam teorema sisa tersebut ialah 3.
Teorema Faktor
Selain materi teorema sisa di atas, adapula materi teorema faktor yang akan saya jelaskan selanjutnya. Teorema faktor merupakan sebuah pembagi yang mempunyai sisa nol (0) untuk dijadikan sebagai faktor suku banyaknya. Untuk itu teorema faktor digunakan dalam mencari sisa pembagian suku banyak.
Apabila suku banyak tidak mempunyai sisa atau memiliki sisa pembagian berupa nol (0), maka tergolong dalam faktor suku banyak. Akan tetapi bila pembaginya mempunyai sisa tidak nol, maka tidak termasuk dalam faktor suku banyak.
Baca juga : Materi Pembulatan Angka dan Bilangan: Cara Membulatkan Beserta Contoh Soal dan Jawabannya
Rumus Teorema Faktor
Banyak siswa mengeluh tidak mampu mengerjakan contoh soal teorema faktor saat ulangan berlangsung. Padahal materinya pun telah disampaikan oleh guru secara terperinci. Lantas apa yang menyebabkan kendala semacam itu? jawabannya tentu saja karena mereka kurang menguasai rumus teorema faktor dengan baik. Maka dari itu, sebelum mulai menghitung kalian perlu memperhatikan beberapa faktor dan aspek berikut:
- Jika suku banyak dapat dinyatakan dalam bentuk f(x), maka faktor dari f(x) jika dan hanya jika f(k) = 0 ialah (x – k).
Dari pernyataan ini dapat disimpulkan bahwa:
- Apabila faktor dari f(x) adalah (x – k), maka hasilnya akan menjadi f(k) = 0.
- Apabila f(k) = 0, maka faktor faktor dari f(x) adalah (x – k).
Agar anda lebih memahami tentang materi teorema sisa dan teorema faktor tersebut, maka saya akan membagikan contoh soal teorema faktornya. Adapun contoh soal dan pembahasannya yaitu sebagai berikut:
Contoh Soal Teorema Faktor
Ada banyak sekali model latihan soal teorema faktor yang sebenarnya bisa kita kerjakan di buku pedoman matematika. Saya yakin guru pun pasti juga akan mengulas rumus teorema sisa maupun teorema faktor secara mendalam. Tapi karena minimnya pemahaman konsep terkadang membuat siswa terus mengeluh. Maka dari itu, sebagai bahan latihan simaklah contoh soal di bawah:
Gunakan teorema faktor untuk menunjukkan bahwa (x – 2) adalah faktor dari f(x) = x³ – 6x² + 12x – 8!
Jawab.
f(x) = x³ – 6x² + 12x – 8 memiliki faktor yaitu (x – 2) yang dapat ditunjukkan menggunakan nilai f(2) = 0. Maka perhitungannya akan menjadi:
f(x) = x³ – 6x² + 12x – 8
f(2) = 2³ – 6(2)² + 12(2) – 8
f(2) = 8 – 24 + 24 – 8
f(2) = 0
Maka dari itu faktor dari f(x) = x³ – 6x² + 12x – 8 adalah (x – 2).
Selain menggunakan cara di atas, kita dapat menggunakan pemfaktoran untuk membuktikan bahwa (x – 2) adalah faktor dari f(x) = x³ – 6x² + 12x – 8. Dari hasil pemfaktoran ini akan diperoleh persamaan seperti di bawah ini:
f(x) = x³ – 6x² + 12x – 8
f(x) = (x – 2)(x² – 4x + 4)
Dalam persamaan di atas diperoleh pangkat 2 sebagai pangkat tertingginya. Maka dari itulah persamaan tersebut dapat difaktorkan lagi menjadi lebih sederhana. Cara memfaktorkan x² – 4x + 4 ini dapat menggunakan cara seperti biasanya. Maka dapat diperoleh hasil seperti di bawah ini:
x² – 4x + 4 = (x – 2)(x – 2)
Dari pembahasan di atas dapat kita peroleh bentuk persamaan f(x) dalam suku tersebut yang berupa:
x³ – 6x² + 12x – 8 = (x – 2)(x – 2)(x – 2)
x³ – 6x² + 12x – 8 = (x – 2)³
Jadi (x – 2) adalah faktor persamaan dari x³ – 6x² + 12x – 8. Maka dari itulah teorema faktor di atas dapat membuktikan bahwa (x – 2) merupakan faktor dari x³ – 6x² + 12x – 8.
Sekian penjelasan mengenai materi teorema sisa dan teorema faktor beserta contoh soal teorema sisa dan contoh soal teorema faktor. Materi teorema faktor dan teorema sisa merupakan jenis teorema yang terdapat dalam suku banyak atau polinomial. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.