Rumus Perpangkatan Aljabar Beserta Contoh Soal – Perpangkatan ialah mengalikan bilangan itu sendiri (bilangan asli) sebanyak berapa kali bilangan tersebut ditunjukkan. Sedangkan aljabar ialah simbol atau lambang dari Matematika. Perpangkatan aljabar ialah perkalian suatu bilangan yang sama secara berulang kali dan berkaitan dengan simbol simbol Matematika. Pada kesempatan kali ini saya akan menjelaskan tentang rumus, cara mudah menyelesaikan perpangkatan aljabar dan contoh soal perpangkatan aljabar. Langsung saja dapat anda simak di bawah ini.
Seperti yang telah kita ketahui bahwa pangkat atau eksponen merupakan suatu bilangan yang letaknya sedikit ke atas dan ukurannya lebih kecil dibandingkan bilangannya. Karena bentuk pangkatnya berupa aljabar, maka pangkat pangkatnya dapat berbentuk variabel. Bagi sebagian siswa tentunya menganggap materi Matematika yang satu ini sulit karena menggunakan beberapa variabel di dalamnya. Tetapi pada kenyataannya tidak sesulit yang anda bayangkan.
Dalam materi Matematika terdapat pembahasan mengenai perpangkatan arjabar. Untuk kategori materi ini memiliki rumus dan cara pengerjaan yang berbeda beda. Untuk itu jika anda menemukan soal soal terkait perpangkatan aljabar, maka dapat menggunakan rumus yang ada. Maka dari itu pengerjaan yang anda lakukan dapat disesaikan dengan baik dan benar. Lantas bagaimana rumus perpangkatan aljabar itu? Bagaimana bentuk contoh soal perpangkatan aljabar itu?
Rumus Perpangkatan Aljabar Beserta Contoh Soal
Pada dasarnya rumus pada perpangkatan aljabar hampir sama dengan rumus perpangkatan bilangan bulat. Secara umum rumus perpangkatan tersebut dapat dinyatakan dalam bentuk seperti dibawah ini:
Berdasarkan rumus diatas dapat kita peroleh rumus perpangkatan aljabar secara umum. Berikut rumusnya yaitu:
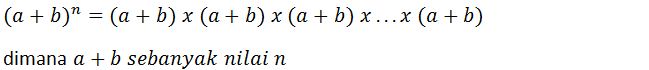
Baca juga : Kumpulan Rumus Matematika SD Kelas 5 Beserta Contoh Soal
Sebelum membahas rumus perpangkatan berbentuk aljabar lebih lanjut, ada beberapa hal yang perlu diperhatikan yaitu:
Berdasarkan bentuk persamaan perpangkatan diatas dapat disimpulkan bahwa kedua persamaan tersebut berbeda. Hal ini dikarenakan pada perpangkatan pertama, n hanya memangkatkan b saja. Sedangkan pada perpangkatan kedua, n memangkatkan a dan b. Misalnya
- (3a)² = 3a x 3a = 9a²
- 3a² = 3 x a x a = 3a²
Kemudian adapula bentuk persamaan perpangkatan bentuk aljabar lainnya yaitu
Kedua bentuk persamaan perpangkatan aljabar di atas juga bebeda. Perbedaannya terletak pada tanda – (minus). Untuk persamaan pertama, n memangkatkan -ab. Sedangkan pada persamaan kedua, n hanya memangkatkan ab tanpa diikuti dengan tanda -(minus).
Cara Menyelesaikan Perpangkatan Aljabar
Rumus perpangkatan berbentuk aljabar ini dapat diterapkan dengan mudah dalam soal soal pangkat dua. Soal tersebut tergolong mudah untuk diselesaikan karena pangkatnya hanya berjumlah 2. Tetapi bagaimana jika jumlah pangkatnya lebih dari 2?
Untuk menyelesaikannya anda dapat menggunakan prinsip segitiga pascal. Tidak heran jika rumus perpangkatan ini juga menerapkan prinsip segitiga pascal seperti berikut:
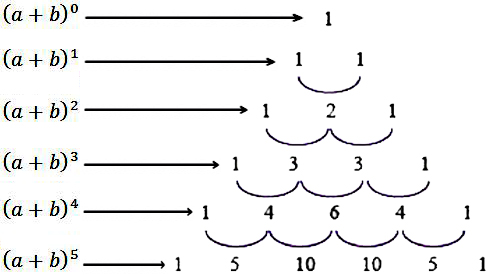
Keterangan:
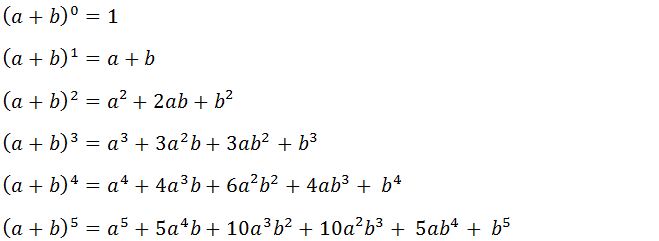
Contoh Soal Perpangkatan Aljabar
Setelah menjelaskan tentang rumus perpangkatan aljabar di atas. Selanjutnya saya akan membagikan contoh soal perpangkatan aljabar terkait rumus di atas. Adapun contoh soal dan pembahasannya yaitu:
Baca juga : Rumus Rumus Pangkat (Perkalian, Pembagian, Pangkat Nol dan Negatif)


Demikianlah penjelasan mengenai rumus perpangkatan aljabar beserta contoh soal perpangkatan aljabar. Untuk menyelesaikan soal soal perpangkatan aljabar, anda harus memahami tanda tanda bilangan dan pola pada segitiga pascal. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.