Cara Menentukan Nilai Stasioner Beserta Contoh Soal – Dalam ilmu Matematika terdapat pembahasan mengenai titik kritis pada penurunan fungsi atau titik stasioner dalam bidang kalkulus. Pengertian titik stasioner ialah sebuah titik yang memiliki kurva turunan pertama dalam grafik dengan nilai sama dengan nol. Adapula yang mengartikan titik stasioner sebagai titik turun ataupun naik tanda berhenti pada sebuah fungsi.
Titik stasioner pada penurunan beberapa fungsi variabel rill memiliki turunan parsial sama dengan nol, dimana letaknya di permukaan grafik. Apakah anda tahu bagaimana cara menentukan stasioner itu? Bagaimana bentuk contoh soal nilai stasioner itu? Apa saja jenis ekstrim fungsi itu?
Untuk menggambarkan titik stasioner dapat dilakukan dengan mudah pada sebuah grafik fungsi yang memuat satu variabel. Hal ini dikarenakan letak titik itu ada di garis titik tangen pararel secara horizontal atau pada sumbu x. Kemudian untuk titik stasioner dalam fungsi dua variabel memiliki nilai yang sama dengan titik grafik pararel antara bidang tangen dengan bidang xy. Dalam materi titik stasioner tersebut terdapat pembahasan lengkap mengenai cara menentukan nilai stasioner, jenis ekstrim fungsi dan contoh soal nilai stasioner itu sendiri. Dengan begitu para siswa dapat memahami materi tersebut lebih secara jelas.
Cara Menentukan Nilai Stasioner Beserta Contoh Soal
Kita tahu bahwa nilai stasioner masih berhubungan dengan turunan fungsi, baik fungsi turun maupun fungsi naik. Cara menentukan stasioner ini dapat dilakukan dengan menyamakan turunannya dengan nol, meskipun nilai turunan pada fungsi turun maupun fungsi naik lebih kecil ataupun lebih besar dari nol (0).
Apabila f(x) diferensiabel dengan f'(a) = 0 di x = a, maka nilai stasioner di x = a ialah f(a) dan titik stasioner dari f(x) ialah titik (a, f(a)). Pada kesempatan kali ini saya akan menjelaskan tentang cara menentukan nilai stasioner beserta contoh soal nilai stasioner. Selain itu saya juga akan membahas tentang jenis ekstrim fungsi lengkap. Untuk lebih jelasnya dapat anda simak di bawah ini.
Seperti yang telah saya jelaskan dalam pengertian titik stasioner di atas bahwa turunan kurva pertama memiliki titik pada grafik yang bernilai sama dengan nol. Dalam hal ini terdapat beberapa persamaan yang menandakan adanya jenis ekstrim fungsi. Untuk itu cara pengerjaan setiap jenis nilai stasionernya memiliki metode yang berbeda beda. Pada umumnya materi nilai stasioner dalam Matematika ini memang perlu dipelajari dan dipahami karena sering muncul dalam soal soal ujian Nasional dan ujian sekolah.
Baca juga : Cara Menghitung Luas Bangun Datar Segi Banyak Beserta Contoh Soal
Latihan Soal Nilai Stasioner
Dalam materi titik stasioner terdapat persamaan f(x) diferensiabel dengan f’(a) = 0 di x = a, maka nilai stasioner di x = a ialah f(a) dan titik stasioner dari f(x) ialah titik (a, f(a)). Cara menentukan nilai stasioner dan cara menyelesaikan contoh soal nilai stasioner tersebut dapat memperhatikan persamaan tersebut. Untuk lebih jelasnya dapat anda perhatikan grafik fungsi di bawah ini:
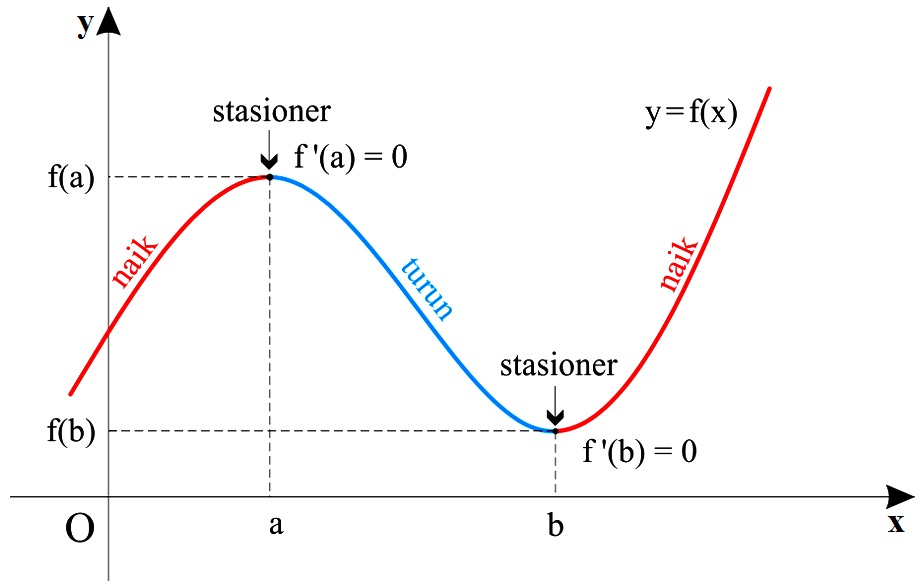
Berdasarkan grafik fungsi di atas dapat kita temukan nilai stasioner di x = a yang berupa f(a) dan nilai stasioner di x = b seperti f(b). Pada titik titik tersebut terdapat nilai turunan pertama yang sama dengan nol. Kemudian untuk titik stasioner pada fungsi f ini dapat berupa titik (a, f(a)) maupun (b, f(b)). Agar anda lebih paham mengenai materi titik stasioner tersebut, maka saya akan membagikan contoh soal terkait materi itu. Berikut contoh soal dan pembahasannya:
1. Diketahui sebuah fungsi x² – 6x. Hitunglah titik stasioner dan nilai stasionernya?
Pembahasan.
Cara menentukan nilai stasioner dari fungsi tersebut dapat dilakukan dengan mencari turunan pertama dari fungsi tersebut. Untuk itu hasilnya akan menjadi:
f'(x) = 2x – 6
f(x) stasioner → f'(x) = 0
2x – 6 = 0
2x = 6
x = 3
Untuk mencapai nilai stasioner tersebut dapat dilakukan ketika x = 2. Maka:
Nilai stasioner : f(3) = (3)² – 6(3) = -9
Titik stasioner : (3,-9)
Jadi fungsi tersebut memiliki titik stasioner (3,-9) dan nilai stasioner yaitu -9.
2. Diketahui sebuah fungsi f(x) = x³ – 4x+ 2. Hitunglah titik stasioner dan titik stasionernya?
Pembahasan.
Contoh soal nilai stasioner di atas dapat diselesaikan dengan langkah langkah seperti di bawah ini:
f(x) = x³ – 27x+ 9
f'(x) = 3x² – 27
f(x) stasioner → f'(x) = 0
3x² – 27 = 0
x² – 9 = 0
(x – 3)(x + 3) = 0
x = 3 atau x = -3
Langkah berikutnya yaitu menentukan nilai stasioner dengan nilai x = 3 maupun x = -3. Maka hasilnya akan menjadi:
Nilai stasioner di x = 3 : f(3) = (3)³ – 27(3)+ 9 = -45
Nilai stasioner di x = -3 : f(-3) = (-3)³ – 27(-3)+ 9 = 63
Titik stasionernya ialah (3,-45) dan (-3,63)
Baca juga : Materi Bilangan Bulat (Pengertian, Operasi Hitung dan Contoh)
Penjelasan di atas merupakan cara menentukan nilai stasioner secara umum. Nilai nilai stasioner tersebut dapat dinamakan dengan bakal dari calon nilai ekstrim. Jenis ekstrim fungsi tersebut dapat dibagi menjadi dua kategori yaitu nilai balik minimum dan nilai balik maksimum. Nilai balik minimum dapat dinamakan dengan nilai minimum lokal ataupun nilai minimum relatif. Sedangkan nilai balik maksimum dapat dinamakan dengan nilai maksimum lokal ataupun nilai maksimum relatif. Dalam sebuah fungsi terdapat jenis ekstrim yang dapat dicari menggunakan dua metode yaitu uji turunan pertama maupun uji turunan kedua. Berikut penjelasan selengkapnya:
Uji Turunan Pertama
Cara menentukan jenis ekstrim fungsi yang pertama dapat menggunakan metode uji turunan pertama. Dalam metode ini terdapat beberapa ketentuan seperti di bawah ini:
Apabila nilai stasioner di x = a ialah f(a). Maka:
- f(a) ialah nilai balik maksimum, apabila:
f ‘(x) > 0 (naik), untuk nilai x < a
f ‘(x) < 0 (turun), untuk nilai x > a - f(a) ialah nilai balik minimum, apabila:
f ‘(x) > 0 (naik), untuk nilai x > a
f ‘(x) < 0 (turun), untuk nilai x < a
Agar anda lebih paham mengenai cara menentukan nilai stasioner dalam jenis ekstrim tersebut. Maka saya akan membagikan contoh soal nilai ekstrim terkait ketentuan dalam uji turunan pertama ini. Berikut contoh soal dan pembahasannya:
Diketahui sebuah fungsi f(x) = x³ – 15x² + 12x + 2. Hitunglah jenis ekstrim fungsi tersebut menggunakan uji turunan pertama?
Pembahasan.
Cara menentukan jenis ekstrim dari fungsi tersebut dapat dilakukan dengan mencari turunan pertama dari fungsinya. Maka:
f'(x) = 3x² – 15x + 12
f'(x) = 0
3x² – 15x + 12 = 0
x² – 5x + 4 = 0
(x – 4)(x – 1) = 0
x = 4 atau x = 1
Nilai stasioner pada x = 4 : f(4) = (4)³ – 15(4)² + 12(4) + 2 = -126
Nilai stasioner pada x = 1 : f(1) = (1)³ – 15(1)² + 12(1) + 2 = 0
Uji Turunan Kedua
Selain penjelasan mengenai cara menentukan nilai stasioner di atas. Selanjutnya saya akan membahas tentang cara menentukan jenis ekstrim fungsi menggunakan uji turunan kedua. Dalam uji turunan yang kedua ini terdapat ketentuan seperti di bawah ini:
Baca juga : Contoh Soal Dilatasi Beserta Pengertian dan Rumus Lengkap
Apabila nilai stasioner di x = a ialah f(a). Maka:
- Nilai balik maksimum berupa f(a), apabila f”(a) < 0.
- Nilai balik minimum berupa f(a), apabila f”(a) > 0.
- Belum dapat menetapkan jenis ekstrim, apabila f”(a) = 0 sehingga jenis ekstrimnya dapat ditentukan menggunakan uji turunan pertama seperti di atas.
Agar anda lebih paham mengenai cara menentukan stasioner dalam jenis ekstrim tersebut. Maka saya akan membagikan contoh soal nilai stasioner terkait ketentuan dalam uji turunan kedua ini. Berikut contoh soal dan pembahasannya:
Diketahui sebuah fungsi f(x) = x³ – 15x² + 12x + 2. Hitunglah jenis ekstrim fungsi tersebut menggunakan uji turunan kedua?
Pembahasan.
Cara menentukan jenis ekstrim dari fungsi tersebut dapat dilakukan dengan mencari turunan pertama dan turunan kedua dari fungsinya. Maka:
f'(x) = 3x² – 15x + 12
f”(x) = 6x – 15
f'(x) = 0
3x² – 15x + 12 = 0
x² – 5x + 4 = 0
(x – 4)(x – 1) = 0
x = 4 atau x = 1
Nilai stasioner pada x = 4 : f(4) = (4)³ – 15(4)² + 12(4) + 2 = -126
Nilai stasioner pada x = 1 : f(1) = (1)³ – 15(1)² + 12(1) + 2 = 0
Kemudian menentukan uji turunan keduanya menggunakan metode seperti di bawah ini:
f”(4) = 6(4) – 15 = 9 > 0
f”(1) = 6(1) – 15 = -9 < 0
Demikianlah penjelasan mengenai cara menentukan nilai stasioner beserta contoh soal nilai stasioner. Selain itu saya juga telah membahas tentang jenis ekstrim fungsi. Titik stasioner dapat diartikan sebagai titik yang memiliki kurva turunan pertama dalam grafik dengan nilai sama dengan nol. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.