Rumus Persamaan Kuadrat Matematika Beserta Contoh Soal – Berdasarkan para ahli, pengertian persamaan kuadrat ialah kalimat terbuka yang memaparkan hubungan antara pangkat tertinggi dan tanda sama dengan (=) pada variabel yang nilainya dua. Bentuk umum dari persamaan kuadrat tersebut ialah y = ax² + bx + c. Untuk menyelesaikan contoh soal persamaan kuadrat biasanya menggunakan rumus pada materi persamaan kuadrat yang ada. Materi Matematika ini sering digunakan dalam soal soal ujian tingkat SMA (Sekolah Menengah Atas) sederajat.
Seperti yang telah kita ketahui bahwa materi persamaan kuadrat yang akan dibahas dalam artikel ini berkaitan dengan variabel. Persamaan tersebut memiliki kuadrat tertinggi yang dihubungkan dengan tanda sama dengan. Maka dari itu kita dapat mencari nilai persamaan tersebut melalui hubungan diantara keduanya. Selain itu jumlah suku yang terdapat dalam persamaan tersebut juga banyak sehingga tidak sesederhana persamaan biasanya.
 |
| Rumus Persamaan Kuadrat Matematika Beserta Contoh Soal |
Persamaan kuadrat tersebut merupakan jenis persamaan yang sering digunakan dalam ilmu Matematika. Adapula yang mengartikan persamaan kuadrat Matematika ini sebagai persamaan suku banyak (polinomial) dimana jumlah pangkatnya ialah dua. Pada kesempatan kali ini saya akan menjelaskan tentang rumus persamaan kuadrat Matematika beserta contoh soal persamaan kuadratnya. Untuk lebih jelasnya dapat anda simak di bawah ini.
Rumus Persamaan Kuadrat Matematika Beserta Contoh Soal
Sebelum membahas tentang rumus dan contoh soal pada materi persamaan kuadrat ini. Saya akan menjelaskan terlebih dahulu mengenai persamaan tersebut. Persamaan kuadrat digambarkan dalam bentuk grafik parabolik dimana koordinatnya berupa x dan y. Maka dari itu persamaan ini dapat dinamakan sebagai persamaan parabola. Adapun bentuk umum persamaan kuadrat Matematika tersebut yaitu:
y = ax² + bx + c
dimana a ≠ 0 dan a, b, c ∈ R
Keterangan:
a = koefisien kuadrat dari x²
x = variabel
b = koefisien linier dari x
c = konstanta
Baca juga : Materi Logika Matematika Beserta Rumus dan Contoh Soalnya
Dalam rumus persamaan kuadrat terdapat nilai koefisien dari a, b dan c diatas. Nilai koefisien tersebut berpengaruh terhadap bentuk parabola dalam koordinat x dan y. Berikut bentuk parabola pada persamaan f(x) = ax² + bx + c sesuai dengan nilai a, b , dan c nya:
Koefisien a
Nilai koefisien a berhubungan dengan pembentukan kurvanya. Dimana kurva parabolanya dapat berbentuk cembung atau cekung sesuai dengan nilai a nya. Apabila a < 0 maka bentuk parabolanya ialah terbuka ke bawah. Sedangkan apabila a > 0 maka bentuk parabolanya adalah terbuka ke atas.
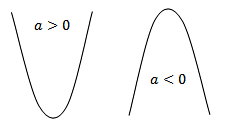 |
| Gambar Kurva Parabola jika a>0 atau a<0 |
Koefisien b
Rumus persamaan kuadrat juga mengandung nilai koefisien b. Bentuk kurva parabola pada koefisien ini memiliki nilai x = -b/2a dimana terdapat posisi x pada sumbu simetri atau puncak parabolanya. Untuk lebih jelasnya dapat anda simak gambar dibawah ini:
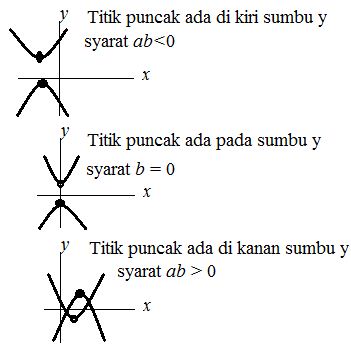 |
| Gambar Kurva Parabola Sesuai dengan Nilai Koefisien b |
Baca juga : Penjumlahan dan Pengurangan Bilangan Pecahan (Cara Mudah)
Koefisien c
Dalam materi persamaan kuadrat juga mengandung nilai koefisien c. Nilai koefisien tersebut berguna dalam menyatakan titik potong antara sumbu y dengan fungsi parabola. Untuk lebih jelasnya dapat anda simak gambar di bawah ini:
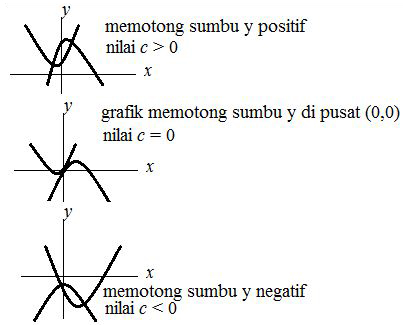 |
| Gambar Kurva Parabola Sesuai dengan Nilai Koefisien c |
Cara Menyelesaikan Persamaan Kuadrat
Cara menyelesaikan persamaan kuadrat dapat dilakukan menggunakan langkah pemfaktoran, rumus ABC maupun kuadrat sempurna. Masing masing cara memiliki rumus persamaannya sendiri. Berikut penjelasan selengkapnya:
Pemfaktoran
Cara menyelesaikan persamaan kuadrat yang pertama melalui metode pemfaktoran. Rumus kuadrat melalui metode pemfaktoran ini berlaku untuk bentuk persamaan ax² + bx + c = 0. Cara ini memiliki ketentuan khusus yaitu apabila dijumlahkan akan bernilai b dan jika dikalikan akan menjadi nilai a x c. Untuk lebih jelasnya dapat anda simak contoh soal persamaan kuadrat di bawah ini:
Faktorkan dan cari penyelesaian dari persamaan kuadrat 2x² + 11x + 12 = 0?
Jawab.
 |
| Jawaban Contoh Soal Persamaan Kuadrat Melalui Pemfaktoran |
Baca juga : Cara Menyelesaikan Persamaan Linier Satu Variabel dan Contoh Soal
Kuadrat Sempurna
Cara menyelesaikan persamaan kuadrat selanjutnya ialah melalui metode kuadrat sempurna. Kuadrat sempurna memiliki bentuk persamaan yang hasilnya ialah bilangan rasional. Adapun rumus persamaan kuadrat menggunakan metode kuadrat sempurna yaitu:
(x + p)² = x² + 2px + p²
Maka diperoleh persamaan :
(x + p)² = q
x + p = ± q
x = -p ± q
Agar anda lebih paham mengenai rumus kuadrat diatas. Saya akan membagikan contoh soal persamaan kuadratnya seperti di bawah ini:
x² + 8x + 7 = 0
Jawab
x² + 8x + 7 = 0
Dapat diubah menjadi persamaan x² + 8x = -7
Ubah menjadi bentuk kuadrat sempurna dengan menambahkan satu angka pada ruas kanan dan kiri. Angka tersebut berasal dari setengah angka koefisien dari x kemudian dikuadratkan yaitu setengah dari 8 = 4, lalu 4² = 16.
Tambahkan angka 16 pada ruas kanan dan kiri sehingga menjadi persamaan:
x² + 8x + 16 = -7 + 16
x² + 8x + 16 = 9
(x + 4)² = 9
x + 4 = √9
x + 4 = 3
x + 4 = ± 3
Maka dari itu x + 4 = 3
x = 3 – 4 = -1
Kemudian x + 4 = -3
x = -3 -4 = -7
Jadi x = -1 atau x = -7
Rumus ABC
Cara menyelesaikan persamaan kuadrat selanjutnya ialah melalui rumus ABC. Adapun rumus ABC yang dapat digunakan yaitu:
 |
| Rumus ABC Dalam Persamaan Kuadrat |
Sekian penjelasan mengenai rumus persamaan kuadrat Matematika beserta contoh soal persamaan kuadrat. Cara menyelesaikan persamaan kuadrat dapat melalui metode pemfaktoran, rumus ABC ataupun melalui kuadrat sempurna. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.


