Rumus Persamaan Garis Singgung Lingkaran Beserta Contoh Soal – Lingkaran menjadi salah satu bangun dua dimensi yang menjadi materi dasar di berbagai jenjang. Di dalamnya, kita bisa menemukan berbagai topik bahasan menarik serta berbeda dari bangun datar lainnya. Kalian hanya akan menjumpai tembereng, juring, irisan, hingga persamaan garis singgung. Masing-masing memiliki pengertian serta rumus dengan tingkat kesulitan berbeda.
Dalam pembahasan kali ini saya akan menjelaskan tentang rumus persamaan garis singgung lingkaran beserta contoh soal. Persamaan lingkaran dalam garis singgung ini mencakup tiga kondisi penting yaitu persamaan garis singgung pada lingkaran yang melalui satu titik didalamnya, garis singgung pada lingkaran yang melalui satu titik di luarnya, dan persamaan garis singgung yang menggunakan gradien (m) tertentu. Masing masing keadaan garis singgung tersebut memiliki cara menghitung yang berbeda beda. Untuk itu penggunaan rumus garis singgung lingkarannya juga berbeda beda.
Sebelum membahas tentang rumus persamaan garis singgung lingkaran. Tentunya kalian harus mengetahui menenai kriteria kedudukan garis dan titik pada sebuah lingkaran terlebih dahulu. Kedudukan garis dan titik ini dapat membantu kita menyelesaikan contoh soal garis singgung lingkaran nantinya. Pasalnya, posisi titik pada lingkaran dipengaruhi oleh kedudukan garis dan titik itu sendiri. Posisi titik ini bisa berada di luar lingkaran, di dalam lingkaran, ataupun pada tengah bangun sekalipun.
Rumus Persamaan Garis Singgung Lingkaran Beserta Contoh Soal
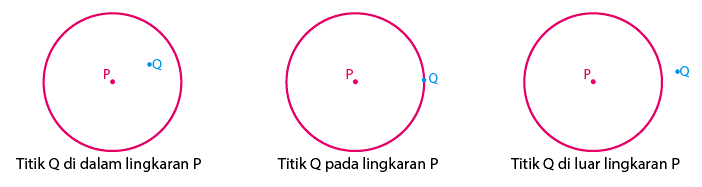
Seperti yang sudah saya jabarkan di atas bahwa anda harus mengetahui letak kedudukan garis dan titik pada lingkaran sebelum lanjut ke tahap rumus persamaan garis singgung lingkarannya. Untuk itu dibawah ini terdapat gambar kedudukan garis dan titik terhadap lingkarannya, baik di luar lingkaran, memotong pada dua titik terhadap lingkaran, ataupuun menyinggung lingkaran (garis memotong pada satu titik lingkaran). Berikut gambar kedudukan persamaan lingkarannya yaitu:
Baca juga : Rumus Persamaan Eksponen Beserta Contoh Soal Eksponen
 |
| Kedudukan Titik Terhadap Lingkaran |
Gambar di atas merupakan ilustrasi kedudukan titik terhadap sebuah lingkaran. Kedudukan ini akan mempengaruhi penggunaan rumus persamaan garis singgung lingkarannya. Maka dari itu sebelum menerapkan rumus persamaan lingkaran ini, anda harus tahu betul letak titiknya.
Contoh soal garis singgung lingkaran sebenarnya bisa kita temukan dengan mudah di buku latihan. Tapi seiring berjalannya waktu siswa pun perlu beradaptasi dengan model latihan soal baru sebagai bekal untuk menghadapi ujian. Dari sinilah muncul inisiatif untuk mencari sendiri materi yang berisi soal serta rumus garis singging lingkaran.
Jika kebetulan kalian belum memahami materi sepenuhnya maka simaklah artikel di bawah sampai selesai. Karena saya akan memberikan penjelasan terkait rumus dan cara menghitung garis singgung pada lingkaran.
Garis Singgung Melewati Sebuah Titik Lingkaran
Rumus persamaan garis singgung lingkaran yang pertama berkaitan dengan garis singgung yang melewati sebuah titik pada lingkaran. Dalam garis singgung ini terdapat sebuah titik pusat P pada lingkaran. Kemudian titik Q dengan koordinat x dan y ingin menyinggung lingkaran tersebut. Untuk itu cara mencari garis singgung yang melalui titik Q terhadap lingkaran tersebut diperlukan persamaan lingkaran agar titik Q dan P dapat saling menyinggung. Perhatikan gambar di bawah ini!
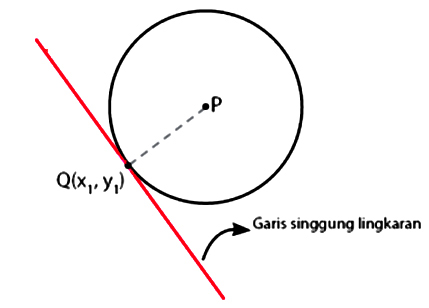 |
| Persamaan Garis Singgung Titik Q Terhadap Lingkaran |
Untuk menentukan garis singgung yang melalui sebuah titik terhadap lingkaran di atas dapat menggunakan beberapa persamaan umum. Bentuk persamaan lingkaran yang diketahui tersebut akan mempengaruhi penggunaan rumusnya. Adapun rumus persamaan garis singgung lingkaran yang melewati sebuah titik yaitu sebagai berikut:
 |
| Tabel Rumus Persamaan Garis Singgung Melewati Sebuah Titik |
Contoh Soal
Hitunglah persamaan garis singgung lingkaran yang mempunyai persamaan lingkaran (x + 3)² + (y – 4)² = 49 melewati titik Q (2, 5)?
Baca juga : Rumus Turunan Trigonometri Beserta Contoh Soal Lengkap
Pembahasan.
Rumus persamaan garis singgung lingkaran yang digunakan ialah (x – h) (x1 – h) + (y – k) (y1 – k) = r² melalui titik Q (2, 5). Maka
(x – h) (x1 – h) + (y – k) (y1 – k) = r²
(x + 3) (2 + 3) + (y – 4) (5 – 4) = 49
(x + 3) (5) + (y – 4) (1) = 49
5x + 15 + y – 4 = 49
5x + y + 11 – 49 = 0
5x + y – 38 = 0
Jadi persamaan garis singgung lingkaran yang melewati titik Q (2, 5) dengan persamaan lingkaran (x + 3)² + (y – 4)² = 49 ialah 5x + y – 38 = 0
Garis Singgung Melewati Sebuah Titik di Luar Lingkaran
Rumus persamaan garis singgung lingkaran selanjutnya berkaitan dengan garis singgung yang melewati sebuah titik di luar lingkaran. Jenis garis singgung tersebut dapat dinamakan dengan garis singgung polar atau garis singgung kutub. Garis singgung pada lingkaran dapat dicari apabila diluar lingkaran terdapat titik (x, y) dengan cara menarik garis lurus menuju titik tadi. Dengan begitu garisnya dapat menyinggung lingkarannya. Untuk lebih jelasnya dapat anda perhatikan gambar di bawah ini:
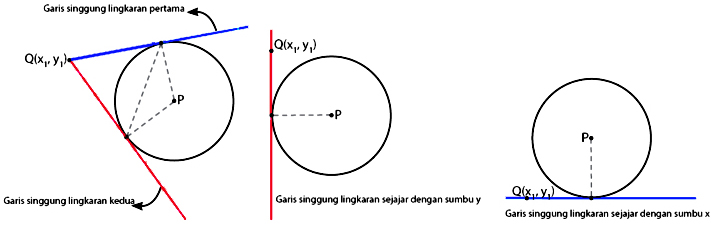 |
| Ilustrasi Garis Singgung Lingkaran Yang Melewati Titik di Luar Lingkaran |
Cara menentukan persamaan garis singgung lingkaran yang melewati titik diluar lingkaran tersebut menggunakan beberapa langkah penting. Adapun langkah langkahnya yaitu sebagai berikut:
- Mencari persamaan lingkaran yang garis singgungnya menggunakan konsep permisalan. Adapun rumusnya yaitu y – y1 = m (x – x1), dimana x dan y adalah titik yang dilalui oleh garis singgung di luar lingkaran. Sedangkan m adalah gradien.
- Setelah itu nilai y disubstitusikan ke persamaan lingkaran di atas sehingga memperoleh variabel x pada persamaan kuadrat.
- Untuk mencari persamaan garis singgung lingkaran selanjutnya ialah mencari nilai diskriminan pada persamaan kuadratnya. Maka nilai D = 0 untuk membuat garis yang dapat menyinggung lingkarannya.
- Langkah selanjutnya ialah menyelesaikan persamaan kuadrat pada langkah sebelumnya.
- Kemudian substitusikan pada persamaan lingkaran y – y1 = m (x – x1).
Contoh Soal
Hitunglah persamaan garis singgung lingkaran yang mempunyai persamaan lingkaran x² + y² = 16 melewati titik (4, 1)?
Pembahasan.
Usahakan titik (4, 1) ini berada diluar lingkaran. Caranya yaitu dengan substitusikan ke persamaannya, maka:
x² + y² = 4² + 1² = 16 + 1 = 17
Nilai x² + y² = 17 > 16, maka titik (4, 1) tersebut terletak di luar lingkaran.
Kemudian hitung persamaan garis singgung lingkarannya dengan menerapkan langkah langkah di atas. Maka hasilnya akan menjadi seperti di bawah ini:
- Membuat permisalan menggunakan persamaan y – y1 = m (x – x1) maka hasilnya akan menjadi:
y – 1 = m (x – 4)
y – 1 = mx – 4m
y = mx – 4m + 1
- Persamaan y = mx – 4m + 1 disubstitusikan ke persamaan x² + y² = 16. Maka hasilnya akan menjadi:
x² + y² = 16
x² + (mx – 4m + 1) ² = 16
x² + m²x² – 8m²x + 2mx + 16m² – 8m + 1 – 16 = 0
(m² + 1)x² – (8m² – 2m)x + (16m² – 8m – 15) = 0
Baca juga : Rumus Identitas Trigonometri Beserta Contoh Soalnya
- Setelah itu menghitung nilai diskriminan D = 0. Dari perhitungan langkah kedua diperoleh nilai:
a = m² + 1; b = 8m² – 2m; c = 16m² – 8m – 15
Maka
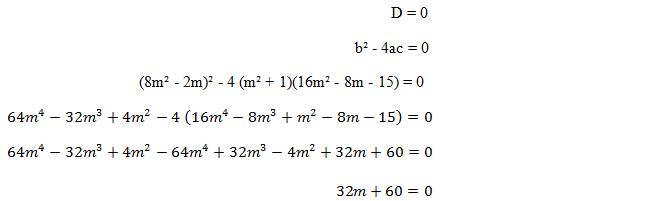
- Mencari nilai m dengan menyelesaikan persamaan 32m + 60 = 0
Maka
32m + 60 = 0
32 m = -60
m = -60/32
m = -15/8
- m = -15/8 disubstitusikan ke persamaan y = mx – 4m + 1
Maka hasilnya
y = mx – 4m + 1
y = -15/8x – 4(-15/8) + 1
y = -15/8x + 15/2 + 1
8y = -15x + 68
15 x + 8y – 68 = 0
Jadi persamaan garis singgung lingkaran yang melewati titik (4,1) dengan persamaan lingkaran x² + y² = 16 ialah 15 x + 8y – 68 = 0
Garis Singgung Lingkaran Dengan Gradien Tertentu
Rumus persamaan garis singgung lingkaran selanjutnya berkaitan dengan garis singgung yang memiliki gradien tertentu. Untuk menentukan garis singgung ini dapat menggunakan beberapa rumus atau persamaan. Rumus tersebut disesuaikan dengan persamaan lingkaran yang sebelumnya telah diketahui. Berikut beberapa rumusnya yaitu sebagai berikut:
 |
| Tabel Rumus Persamaan Garis Singgung Dengan Gradien Tertentu |
Contoh Soal
Diketahui garis singgung lingkaran memiliki gradien 4 dengan persamaan lingkaranya x² + y² + 16. Tentukan persamaan garisnya?
Pembahasan.
Gunakan rumus persamaan garis singgung lingkaran yaitu y = mx ± r√m²+1. Maka:
y = mx ± r√m²+1
y = 4x ± 4 √4²+1
y = 4x ± 12
Jadi persamaan garis singgung lingkaran yang bergradien 4 dengan persamaan lingkaran x² + y² = 16 ialah y = 4x + 12 atau y = 4x -12.
Sekian penjelasan mengenai rumus persamaan garis singgung lingkaran beserta contoh soal. Rumus pada garis singgung tersebut tergantung pada jenis persamaan lingkaran yang diketahui. Semoga artikel ini dapat menambah ilmu anda dan selamat belajar.


