Contoh Soal Dot Product (Perkalian Titik) dalam Vektor – Perkalian vektor tidak hanya dilakukan dengan metode skalar saja. Namun perkalian vektor juga dapat dilakukan dengan menggunakan vektor lainnya. Perkalian vektor dengan vektor lainnya dapat dilakukan dengan dua cara yaitu perkalian silang (cross product) dan perkalian titik (dot product). Apa pengertian dot product itu? Bagaimana rumus dot product? Pengertian perkalian titik dan rumus perkalian titik tentunya berbeda dengan perkalian silang. Untuk itu sifat sifat dot product dengan cross product serta cara mengalikan vektor dengan vektor tersebut juga berbeda. Apakah anda tahu bagaimana sifat sifat perkalian titik itu?
Pengertian dot product (perkalian titik) dua buah vektor ialah perkalian pada vektor pertama (A) yang terjadi antara salah satu besar vektor (A) dengan vektor yang kedua (B). Dengan kata lain pengertian perkalian titik ialah perkalian antara dua vektor yang menghasilkan sebuah skalar. Dari pengertian tersebut terlihat jelas bahwa perkalian titik antar vektor memiliki hasil yang nilainya skalar. Perkalian titik ini memiliki simbol “.” atau dibaca dot. Untuk menyelesaikan contoh soal dot product (perkalian titik) dapat dilakukan dengan menggunakan sifat sifat dot product dalam vektor. Sifat sifat perkalian titik antara dua vektor tersebut merupakan hal dasar yang harus diketahui dan dipahami sebelum mengerjakan soal soal terkait perkalian vektor.
Perkalian titik dapat dinamakan dengan skalar product atau perkalian skalar, karena materi dot product ini menghasilkan nilai yang berupa skalar. Dalam materi perkalian titik (dot product) terdapat pembahasan mengenai persamaan dot product, sifat sifat dot product, dan cara menyelesaikan contoh soal perkalian titik. Pada kesempatan kali ini saya akan membagikan contoh soal dot product (perkalian titik) dalam vektor. Untuk lebih jelasnya dapat anda simak di bawah ini.
Contoh Soal Dot Product (Perkalian Titik) dalam Vektor
Dua buah vektor a dan b yang dikalikan dengan metode dot product (perkalian titik) dapat dinotasikan dalam bentuk a . b. Perkalian titik ini melibatkan dua buah vektor sehingga tidak dapat disamakan dengan perkalian aljabar yang melibatkan bilangan. Di bawah ini terdapat notasi dua buah vektor yang bentuknya seperti berikut:
a = [a₁, a₂, a₃]
b = [b₁, b₂, b₃]
Baca juga : Materi Hiperbola Matematika Beserta Rumus dan Contoh Soal
Antara a dan b tersebut terdapat sudut berupa θ. Jika dinyatakan dalam bentuk gambar, maka hasilnya akan menjadi seperti berikut:
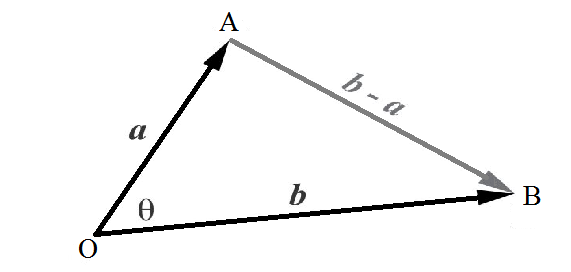
Dari gambar di atas dapat diketahui persamaan baru untuk menyelesaikan contoh soal dot product yang tersedia. Kita dapat menggunakan aturan cosinus di dalamnya, maka hasilnya akan menjadi:
|b – a|² = |a|² + |b|² – 2|a||b|cos θ
|a||b|cos θ = ½ (|a|² + |b|² – |b – a|²) (*)
Persamaan di atas dapat disubstitusikan hingga menjadi persamaan di bawah ini:
|a|² = a₁² + a₂² + a₃²
|b|² = b₁² + b₂² + b₃²
|b – a|² = (b₁ – a₁)² + (b₂ – a₂)² + (b₃ – a₃)²
Dalam materi dot product dalam vektor di atas dapat kita sederhanakan pada ruas kanan persamaan (*). Maka hasilnya menjadi:
|a||b|cos θ = a₁b₁ + a₂b₂ + a₃b₃ (**)
Hubungan antara komponen vektor, panjang dan sudut secara bersamaan dapat dijelaskan menggunakan persamaan dot product yang terakhir ini. Dari penjelasan diatas dapat digunakan untuk memperoleh pengertian dot product dua vektor yang didominasi dengan persamaan perkalian titik tersebut. Persamaan ini digunakan untuk menyelesaikan contoh soal dot product yang tersedia.
Baca juga : Rumus Integral Parsial dan Integral Substitusi Beserta Contoh
Apabila vektor vektor a dan b nilainya tidak nol. Maka penulisan dot product (perkalian titik) antara a dan b ialah a . b. Untuk itu persamaannya akan seperti di bawah ini:
a . b = |a||b|cos θ
Keterangan:
|a| = panjang a
|b| = panjang b
θ = sudut antara a dan b
Penulisan persamaan (**) akan menjadi seperti berikut:
a . b = a₁b₁ + a₂b₂ + a₃b₃
Agar anda lebih paham mengenai materi dot product dalam vektor tersebut, maka saya akan membagikan contoh soal dot product beserta pembahasannya. Berikut contoh soalnya yaitu:
Contoh Soal
1. Diketahui dua vektor u dan v besarnya |u| = 6 dan |v| = 9 serta besar sudut yang terbentuk yaitu 60º. Hitunglah nilai u . v?
Pembahasan.
Contoh soal perkalian titik dua vektor tersebut dapat diselesaikan dengan rumus dot product seperti di bawah ini:
u . v = |u||v|cos 60°
= 6 . 9 . ½
= 27
2. Pada R³ terdapat vektor vektor yang berupa p dan q. Apabila p = 3i – 4j + 5k dan q = 4i – 2k. Maka hitunglah nilai p . q?
Pembahasan.
Contoh soal perkalian titik dua vektor tersebut dapat diselesaikan dengan langkah langkah di bawah ini:
p = [3, -4, 5]
q = [4, 0, -2]
Maka,
p . q = 3 . 4 + (-4) . 0 + 5 . (-2)
= 12 + 0 – 10
= 2
Baca juga : Rumus Modus Data Tunggal dan Kelompok Beserta Contoh Soal
Untuk menyelesaikan contoh soal dot product pada dasarnya dapat dilakukan dengan menggunakan sifat sifat perkalian titik. Perkalian titik memiliki beberapa sifat apabila bilangan/skalarnya berupa k, vektornya berupa a, b dan c. Untuk itu sifatnya akan menjadi seperti di bawah ini:
- a . a = |a|²
- a . b = b . a
- a . (b + c) = a . b + a . c
- a . (kb) = k(a . b) = (ka) . b
Catatan:
Sudut 90º akan terbentuk jika dua buah vektor saling tegak lurus.
Sudut 0º akan terbentuk jika dua buah vektor saling searah.
Sudut 180º akan terbentuk jika dua buah vektor saling berlawanan arah.
cos θ > 0 apabila θ lancip.
cos θ < 0 apabila θ tumpul.
Dari kesimpulan di atas, kita dapat menyelesaikan contoh soal dot product dengan beberapa ketentuan seperti di bawah ini:
Misalkan vektornya berupa a dan b, kemudian kedua vektor ini membentuk sudut θ. Maka persamaan perkalian titiknya akan menjadi seperti berikut:
- a . b = 0, apabila a tegak lurus dengan b.
- a . b = |a||b|, apabila a searah dengan b.
- a . b = -|a||b|, apabila a berlawanan arah dengan b.
- a . b > 0, apabila θ lancip (0 < θ < 90°).
- a . b < 0, apabila θ tumpul (90º < θ < 180°)
Agar anda lebih paham mengenai materi dot product dalam vektor tersebut, maka saya akan membagikan contoh soal perkalian titik beserta pembahasannya. Berikut contoh soalnya yaitu:
Contoh Soal
Diketahui u = [4, 2, -3] dan v = [5, 2, k]. Supaya kedua vektor ini saling tegak lurus, maka hitunglah nilai k nya?
Pembahasan.
Contoh soal dot product dua vektor ini dapat diselesaikan dengan langkah langkah seperti di bawah ini:
u yang tegak lurus dengan v memiliki ketentuan persamaan u . v = 0. Untuk itu:
u . v = 0
4 . 5 + 2 . 2 + (-3) . k = 0
20 + 4 – 3k = 0
24 – 3k = 0
3k = 24
k = 8
Demikianlah contoh soal dot product (perkalian titik) dalam vektor yang dapat saya bagikan. Dalam materi perkalian titik ini terdapat pembahasan tentang pengertian dot product, sifat sifat dot product dan cara menyelesaikan contoh soal perkalian titik. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi dot product di atas.


