Rumus Pythagoras Segitiga Siku Siku Beserta Contoh – Bangun datar segitiga siku siku sering kali digunakan untuk menjabarkan rumus yang berkaitan dengan pythagoras. Apa itu pythagoras? Tentunya anda sudah tidak asing lagi dengan rumus yang satu ini. Ketika di bangku sekolah tentunya anda sudah di ajarkan mengenai materi pythagoras dalam segitiga siku siku. Materi tersebut memiliki rumus yang hanya dapat digunakan jika bentuk segitiganya siku siku.
Secara sederhana rumus pythagoras merupakan hasil perbandingan antara ketiga sisi pada segitiga siku siku. Pythagoras tersebut sering kali dapat kita jumpai dalam kisi kisi ujian Matematika, baik ujian Nasional maupun ujian sekolah. Lalu bagaimana rumus pythagoras itu? Bagaimana cara menyelesaikan contoh soal pythagoras?
Rumus pada pythagoras pada umumnya telah ditemukan oleh ilmuan bernama Pythagoras (ahli Matematika yang berasal dari Yunani). Hasil penemuan tersebut diberi nama pythagoras. Rumus ini merupakan jenis rumus yang berguna untuk menghitung panjang sisi dalam segitiga siku siku. Kali ini saya akan menjelaskan tentang rumus pythagoras dalam segitiga siku siku beserta contoh soal pythagoras. Untuk lebih jelasnya dapat anda simak di bawah ini.
Rumus Pythagoras Segitiga Siku Siku Beserta Contoh
Materi pythagoras merupakan salah satu materi Matematika yang sering dianggap sulit oleh beberapa siswa. Materi ini sebenarnya dapat dipelajari dengan mudah karena memiliki rumusnya sendiri. Rumus pythagoras tersebut dapat digunakan untuk menghitung panjang salah satu sisi pada bangun segitiga siku siku. Namun rumus ini tidak dapat digunakan jika bangun segitiganya tidak siku siku.
Rumus untuk menghitung pythagoras memiliki nama lain yaitu teorema pythagoras ataupun dalil pythagoras. Dibawah ini terdapat bunyi dari dalil pythagoras atau teorema pythagoras yaitu:
“Dalam segitiga siku siku, ukuran sisi terpanjang (sisi miring) sama dengan kuadrat dari sisi sisi lainnya.”
Rumus pythagoras menggambarkan hubungan yang terjadi antara sisi sisi dalam segitiga siku siku. Hasil dari panjang sisi miringnya merupakan jumlah dari kuadrat kedua sisi lainnya. Berikut rumusnya:
a² + b² = c²
Biasanya rumus pythagoras berguna untuk menghitung hal hal yang bersifat geometri. Misalnya digunakan untuk mencari keliling segitiga siku siku yang panjang sisi miringnya belum diketahui. Rumus ini memang sedikit dilupakan karena soal soalnya tidak secara langsung menanyakan untuk mencari sisi miring dalam segitiga siku siku. Untuk lebih memahami rumus tersebut, anda dapat memperhatikan gambar segitiga di bawah ini:
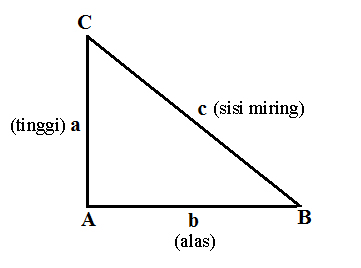
Berdasarkan gabar diatas dapat diperoleh rumus pythagoras seperti di bawah ini :
sisi BC kuadrat = sisi AC kuadrat + sisi AB kuadrat
BC² = AC² + AB²
Baca juga : Pengertian dan Operasi Bilangan Cacah
Adapula rumus lain dalam pythagoras yang dapat digunakan untuk mencari sisi alas, sisi samping tinggi ataupun sisi miringnya. Adapun rumusnya yaitu:
b² = c² – a² (mencari sisi alas)
a² = c² – a² (mencari sisi samping tinggi)
c² = a² + b² (mencari sisi miring)
Rumus pythagoras tidak hanya berguna untuk mencari keliling segitiga yang salah satu sisinya belum diketahui (sisi alas/miring/tinggi). Melainkan dapat digunakan untuk menghitung keliling trapesium juga. Di bawah ini terdapat pola angka dalam teorema pythagoras yaitu:

Keterangan pola angka teorema pythagoras di atas:
a = Sisi tinggi segitiga
b = Sisi alas segitiga
c = Sisi miring segitiga
Contoh Soal Rumus Pythagoras
Agar anda lebih memahami materi pythagoras ini. Maka saya akan membagikan contoh soal terkait pythagoras berdasarkan rumus di atas. Adapun contoh soal dan pembahasannya yaitu:
1. Perhatikan gambar segitiga siku siku berikut!
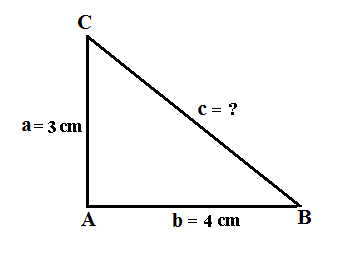
Jika diketahui sisi sisi segitiga seperti pada gambar di atas. Berapakah besar sisi miringnya?
Pembahasan
Diketahui: AC (a) = 3 cm; AB (b) = 4 cm
Ditanyakan: BC (c) = ?
Jawab.
Contoh soal ini dapat diselesaikan dengan rumus pythagoras seperti berikut:
a² + b² = c²
3² + 4² = c²
9 + 16 = c²
c² = 25
c = √25
c = 5 cm
Baca juga : Pengertian dan Contoh Bilangan Prima Lengkap
2. Perhatikan gambar segitiga siku siku di bawah ini!
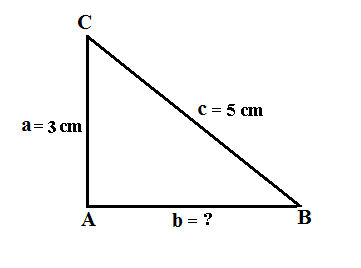
Jika diketahui sisi sisi segitiga seperti pada gambar di atas. Berapakah besar sisi alasnya?
Pembahasan
Diketahui: AC (a) = 3 cm; BC (c) = 5 cm
Ditanyakan: AB (b) = ?
Jawab.
Contoh soal pythagoras tersebut dapat diselesaikan dengan rumus yakni:
b² = c² – a²
= 5² – 3²
= 25 – 9
b² = 16
b = √16
b = 4 cm
3. Perhatikan gambar berikut!
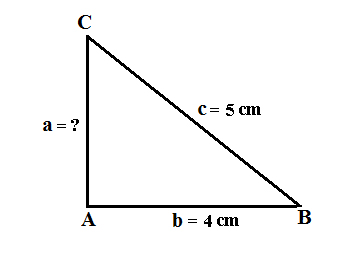
Jika diketahui sisi sisi segitiga seperti pada gambar di atas. Berapakah besar sisi tingginya?
Pembahasan
Diketahui: AB (b) = 4 cm; BC (c) = 5 cm
Ditanyakan: AC (a) = ?
Jawab.
Contoh soal tersebut dapat diselesaikan dengan rumus pythagoras seperti di bawah ini:
a² = c² – b²
= 5² – 4²
= 25 – 16
a² = 9
a = √9
a = 3 cm
Demikianlah penjelasan mengenai rumus pythagoras pada segitiga siku siku beserta contohnya. Konsep teorema pythagoras berlaku hanya untuk bangun datar segitiga siku siku saja. Semoga artikel ini dapat bermanfaat untuk anda dan terima kasih telah membaca materi pythagoras di atas.

Komentar ditutup.