6 Sifat Persamaan Garis Lurus, Rumus, dan Contoh Soalnya – Persamaan garis menjadi salah satu materi yang wajib kita pelajari. Tapi ternyata masih ada yang bertanya bagaimana cara menyelesaikan contoh soal persamaan garis lurus. Ketidaktahuan tersebut disebabkan karena minimnya literasi serta pemahaman terkait rumus serta sifat sifat persamaan garis lurus. Padahal fungsi dan implementasinya sendiri bisa dijumpai dalam kehidupan sehari hari. Inilah alasan mengapa siswa harus mempelajari materi tersebut.
Bagaimana sifat sifat persamaan garis lurus itu? Bagaimana contoh soal persamaan garis lurus itu? Apa itu garis lurus? Pengertian garis lurus ialah garis dengan kemiringan di masing masing ruas yang sama atau perbandingan yang sama antara selisih koordinat x dengan selisih koordinat y (kemiringan/gradien/koefisien arah). Kita dapat mempelajari materi persamaan garis lurus ini dengan cara mempelajari koordinat kartesius terlebih dahulu.
Pada dasarnya materi persamaan garis lurus terdiri dari berbagai pembahasan. Baik itu rumus hitung, sifat sifat, serta latihan soalnya memegang peran penting dalam proses pembelajaran. Bagaimana rumus persamaan garis lurus itu? Pada kesempatan kali ini saya akan menjelaskan tentang sifat sifat persamaan garis lurus dan contoh soal persamaan garis lurus. Untuk lebih jelasnya dapat anda simak di bawah ini.
6 Sifat Persamaan Garis Lurus, Rumus, dan Contoh Soalnya
Persamaan garis lurus yang melalui titik (0, c) atau sumbu y (x = 0) dan gradiennya diketahui dapat memiliki rumusnya sendiri. Adapun rumus persamaan garis lurus yang digunakan yaitu:
y = mx + c
Keterangan:
m = Gradien atau kemiringan atau koefiesien arah, dimana m ≠ 0
c = Konstanta
Baca juga : Rumus Perkalian Pangkat dan Contoh Soalnya
Jika dua persamaan garis lurus atau lebih diketahui, maka sifat sifat persamaan garis lurus di dalamnya dapat ditentukan. Sifat sifat ini dapat digunakan untuk menyelesaikan contoh soal persamaan garis lurus yang ada. Di bawah ini terdapat sifat sifat pada materi persamaan garis lurus yaitu meliputi:
Persamaan Garis Lurus yang Sejajar Sumbu x
Sifat sifat persamaan garis lurus dipengaruhi oleh posisi atau letak berupa koordinat. Maka dari itu, kita pun juga harus mampu membaca diagram koordinat dengan baik dan benar.
Garis AB (![]() ) yang sejajar sumbu x dapat digambarkan dalam bentuk seperti pada gambar si bawah:
) yang sejajar sumbu x dapat digambarkan dalam bentuk seperti pada gambar si bawah:
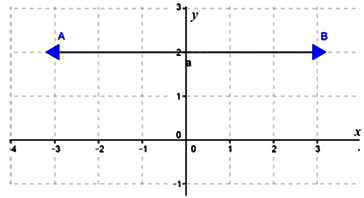
Berdasarkan persamaan garis y = 2 di atas dapat kita ketahui bahwa titik A berada di koordinat (-3, 2) dan B berada di koordinat (3, 2). Dari sini dapat kita lihat bahwa kedua titik ini memiliki ordinat (y) yang sama yakni 2. Maka dari itu garis yang sejajar sumbu x memiliki ciri ciri yaitu ordinat (y) yang dimiliki oleh titik tersebut sama. Oleh karena itu persamaan garisnya memiliki bentuk umum y = k, dimana k = Konstanta.
Persamaan Garis Lurus yang Sejajar Sumbu y
Sifat sifat persamaan garis lurus selanjutnya berlaku untuk yang sejajar sumbu y. Garis AB (![]() ) yang sejajar sumbu y dapat dinyatakan dalam bentuk gambar seperti di bawah ini:
) yang sejajar sumbu y dapat dinyatakan dalam bentuk gambar seperti di bawah ini:
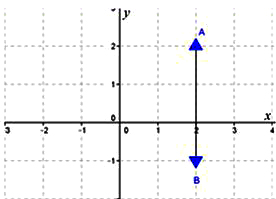
Berdasarkan persamaan garis x = 2 di atas dapat kita ketahui bahwa titik A berada di koordinat (2, 2) dan B berada di koordinat (2, -1). Dari sini dapat kita lihat bahwa kedua titik ini memiliki absis (x) yang sama yakni 2. Maka dari itu garis yang sejajar sumbu y memiliki ciri ciri yaitu absis (x) yang dimiliki oleh titik tersebut sama. Oleh karena itu persamaan garisnya memiliki bentuk umum x = k, dimana k = Konstanta.
Baca juga : Contoh Soal Bilangan Berpangkat dan Jawabannya
Persamaan Garis Lurus yang Saling Sejajar
Sifat sifat persamaan garis lurus selanjutnya berlaku untuk yang saling sejajar. Untuk lebih jelasnya perhatikan gambar berikut:
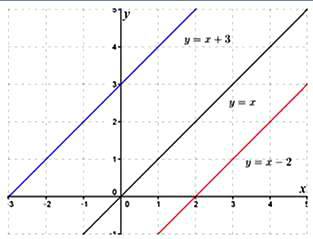
Dalam gambar di atas dapat kita lihat bahwa ruas garis y = x – 2, y = x dan y = x + 3 memiliki kedudukan saling sejajar. Karena meskipun kedua ujungnya diperpanjang maka tidak akan pernah berpotongan. Pembentukan y = x – 2 ini berasal dari penggeseran sumbu y sebanyak 2 satuan ke bawah dari grafik y = x.
Sedangkan pembentukan y = x + 3 ini berasal dari penggeseran sumbu y sebanyak 3 satuan ke atas dari grafik y = x. Maka dari itu dapat kita simpulkan bahwa apabila nilai koefisien x atau nilai a sama akan menghasilkan persamaan y = ax + b dengan y = ax + c yang sejajar.
Persamaan Garis Lurus yang Tegak Lurus
Sifat sifat persamaan garis lurus selanjutnya berlaku untuk yang tegak lurus. Untuk lebih jelasnya perhatikan gambar berikut:
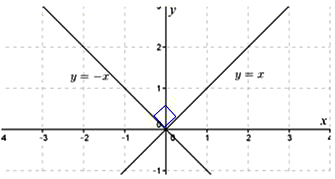
Berdasarkan gambar di atas dapat kita lihat bahwa persamaan y = x berpotongan tegak lurus dengan persamaan y = -x. Kedua persamaan yang saling tegak lurus ini menghasilkan sudut siku siku (90°) pada perpotongan kedua garisnya. Maka dari itu persamaan garis y = ax + b dengan y = (-1/a)x + c akan saling berpotongan tegak lurus.
Persamaan Garis Lurus yang Berpotongan
Sifat sifat persamaan garis lurus selanjutnya ialah saling berpotongan. Apabila dua buah garis lurus tidak saling sejajar, maka dapat dikatakan bahwa keduanya saling berpotongan. Contohnya dua persamaan garis yang diketahui berbentuk y = cx + d dan y = ax + b. Setiap persamaan mempunyai koefisien x yang berbeda (a ≠ c), maka keduanya dapat dinyatakan berpotongan.
Pada sifat persamaan garis lurus yang saling tegak lurus tentunya sudah pasti saling berpotongan. Tetapi dua buah persamaan yang saling berpotongan belum tentu membentuk sudut 90° atau tegak lurus. Maka dari itu dapat disimpulkan bahwa salah satu kedudukan garis saling berpotongan ialah garis saling tegak lurus.
Persamaan Garis Lurus yang Berimpit
Sifat sifat persamaan garis lurus selanjutnya ialah saling berimpit. Apabila kedua garis memiliki dua titik potong paling sedikit, maka dapat dikatakan bahwa garis tersebut saling berimpit. Contohnya persamaan garis px + qy = r yang berimpit dengan ax + by = c. Kedua garis yang saling berimpit ini memiliki hubungan seperti di bawah ini:
a/p = b/q = c/r
Kedua persamaan garis ini memiliki perbandingan suku yang sejenis sehingga dapat dikatakan sebanding. Menurut saya, sifat sifat persamaan garis lurus satu ini begitu penting untuk dilewatkan.
Contoh Soal Persamaan Garis Lurus
Agar anda lebih paham mengenai materi persamaan garis lurus tersebut, maka saya akan membagikan contoh soal terkait materi ini. Berikut contoh soal dan pembahasanya:
Tentukan persamaan garis yang sejajar garis y = 2?
Pembahasan.
Persamaan garis y = 2 akan memiliki hubungan yang saling sejajar dengan garis y = k. Maka dari itu garis ini saling sejajar dengan sumbu y atau x = 0.
Ada banyak sekali contoh serta latihan soal persamaan garis lurus yang bisa kita kerjakan. Selain dari buku, internet menyediakan sumber belajar tanpa batas kepada siswa. Berbagai model soal menyesuaikan sifat sifat persamaan garis lurus di atas pun tersedia.
Demikianlah penjelasan mengenai sifat sifat persamaan garis lurus dan contoh soal persamaan garis lurus. Persamaan garis lurus dapat saling berkaitan satu sama lain dengan menggunakan sifat sifat seperti di atas. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.