Contoh Soal Pertidaksamaan Eksponen Beserta Cara Menyelesaikannya – Materi pertidaksamaan eksponen tentunya sudah tidak asing lagi bagi kita. Materi ini berisi pembahasan mengenai sifat sifat pertidaksamaan eksponen dan metode penyelesaiannya. Namun bukan hal mengejutkan apabila sejumlah siswa masih menganggapnya sulit.
Cara membedakan persamaan dan pertidaksamaan eksponen sebenarnya cukup sederhana. Apabila ada tanda hubung berupa (=) maka itu adalah bentuk persamaan. Tapi kalau tanda yang dipakai adalah <, >, ≠, ≤ ataupun ≥ maka itu adalah soal pertidaksamaan eksponen. Lalu bagaimana cara menyelesaikan contoh soal demikian? kita akan mempelajari rumusnya.
Contoh Soal Pertidaksamaan Eksponen Beserta Cara Menyelesaikannya
Tanda penghubung yang digunakan oleh persamaan dan pertidaksamaan eksponen dapat digunakan sebagai pembeda di antara keduanya. Maka dari itu dalam materi ini kita akan menggunakan tanda <, >, ≠, ≤ ataupun ≥ karena membahas tentang pertidaksamaan eksponen. Materi pertidaksamaan eksponen ini memiliki rumus serta karakteristik masing-masing.
Sifat sifat pertidaksamaan eksponen tersebut dapat kita jadikan sebagai dasar rumus yang sangat bermanfaat. Cara menyelesaikan pertidaksamaan eksponen tidak jauh berbeda dengan persamaan eksponen. Pertidaksamaan eksponen ini memiliki karakteristik yaitu penggunaan tanda pertidaksamaan pada kedua fungsi bilangan berpangkat.
Baca juga : Rumus Pertidaksamaan Logaritma dan Contoh Soalnya
Tanda pertidaksamaan yang dimaksud ialah lebih dari (>), kurang dari (<), lebih dari/sama dengan (≥) ataupun kurang dari/sama dengan (≤). Apakah sampai di sini kalian sudah memiliki sedikit gambaran? Pada kesempatan kali ini saya akan membagikan contoh soal pertidaksamaan eksponen beserta cara menyelesaikan pertidaksamaan eksponen.
Sifat dan Rumus Pertidaksamaan Eksponen
Sebelum menyelesaikan contoh soal pertidaksamaan eksponen di bawah, anda harus memahami beberapa sifat yang ada di dalam materi ini. Mengapa demikian? seperti yang sudah saya jelaskan bahwa sifat saa seperti rumus hitung.
Meskipun kita bisa menjumpainya di LKS maupun buku pedoman matematika. Tapi faktanya asih banyak siswa yang kesulitan menghafalnya. Adapun sifat sifat pertidaksamaan eksponen yang dapat digunakan yaitu meliputi:
Untuk a ≥ 1 memiliki sifat sifat:
- aᶠ⁽ˣ⁾ < aᶢ⁽ˣ⁾ → f(x) < g(x)
- aᶠ⁽ˣ⁾ > aᶢ⁽ˣ⁾ → f(x) > g(x)
- aᶠ⁽ˣ⁾ ≤ aᶢ⁽ˣ⁾ → f(x) ≤ g(x)
- aᶠ⁽ˣ⁾ ≥ aᶢ⁽ˣ⁾ → f(x) ≥ g(x)
Untuk a < a < 1 memiliki sifat sifat:
- aᶠ⁽ˣ⁾ < aᶢ⁽ˣ⁾ → f(x) > g(x)
- aᶠ⁽ˣ⁾ > aᶢ⁽ˣ⁾ → f(x) < g(x)
- aᶠ⁽ˣ⁾ ≤ aᶢ⁽ˣ⁾ → f(x) ≥ g(x)
- aᶠ⁽ˣ⁾ ≥ aᶢ⁽ˣ⁾ → f(x) ≤ g(x)
Contoh Soal Pertidaksamaan Eksponen
Agar anda lebih paham mengenai materi pertidaksamaan eksponen seperti cara menyelesaikan pertidaksamaan eksponen dan sifat sifat pertidaksamaan eksponen di atas. Maka saya akan membagikan contoh soal terkait materi tersebut yaitu diantaranya:
1. Tentukan nilai x yang memenuhi pertidaksamaan eksponen 5²ˣ ‾ ¹ < 1?
Pembahasan.
5²ˣ ‾ ¹ < 1
5²ˣ ‾ ¹ < 5⁰
2x – 1 < 0
2x < 1
x < ½
Jadi nilai x yang memenuhi pertidaksamaan eksponen 5²ˣ ‾ ¹ < 1 ialah x = ½.
Baca juga : 6 Sifat Persamaan Garis Lurus dan Contoh Soalnya
2. Tentukan himpunan penyelesaian dari pertidaksamaan eksponen 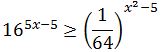 ?
?
Pembahasan.
Contoh soal pertidaksamaan eksponen ini dapat diselesaikan dengan mudah. Adapun cara menyelesaikan pertidaksamaan eksponen seperti di bawah ini:
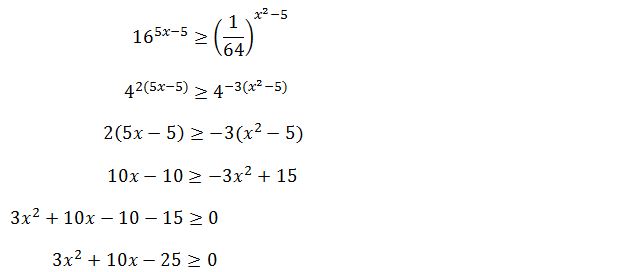
Pertidaksamaan dibuat sama dengan nol. Sehingga:
3x² + 10x – 25 = 0
(3x – 5)(x + 5) = 0
3x – 5 = 0 atau x + 5 = 0
x = 5/3 x = 5
Setelah itu daerah penyelesaiannya dapat ditentukan agar dapat memenuhi pertidaksamaan seperti di bawah ini:
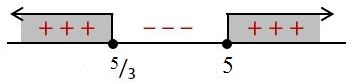
Dari pengujian daerah penyelesaian pertidaksamaan eksponen seperti garis bilangan di atas dapat diperoleh hasil yaitu x ≤ 5/3 atau x ≥ 5.
Sekian contoh soal pertidaksamaan eksponen beserta cara menyelesaikan pertidaksamaan eksponen yang dapat saya bagikan. Pertidaksamaan eksponen ini dapat diselesaikan dengan cara yang tidak jauh berbeda dengan persamaan eksponen. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.