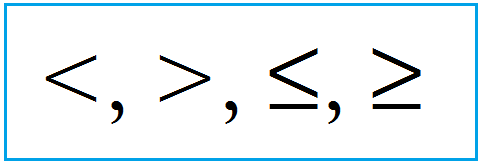
Rumus Pertidaksamaan Logaritma dan Contoh Soalnya – Mampu mengerjakan soal pertidaksamaan logaritma menjadi tantangan berat bagi siswa. Banyak yang gagal lantaran kurang memahami sifat, ciri ciri, hingga rumus hitungnya. Pertidaksamaan logaritma sendiri bisa diartikan sebagai bentuk lain dari persamaandengan tanda “<, >, ≤, ≥” sebagai pengganti tanda “=”. Tanda tanda tersebut merupakan ciri khas dari pembelajaran pertidaksamaan tersebut.
Seperti yang telah kita ketahui bahwa dalam materi pertidaksamaan logaritma terdapat beberapa hal yang dibahas. Pembahasan tersebut yaitu rumus pertidaksamaan logaritma, sifat sifat pertidaksamaan logaritma, contoh soal pertidaksamaan logaritma dan pengertian pertidaksamaan logaritma itu sendiri. Pertidaksamaan logaritma ini memiliki hubungan dengan bilangan pokok atau basis logaritma yang cukup erat.
Rumus Pertidaksamaan Logaritma dan Contoh Soalnya
Materi pertidaksamaan logaritma ini pada dasarnya telah kita pelajari ketika di bangku sekolah. Materi ini juga sering muncul dalam soal soal ujian Matematika, baik ujian Sekolah maupun ujian Nasional. Bagaimana sifat sifat pertidaksamaan logaritma itu?
Seperti yang telah kita ketahui bahwa pengertian pertidaksamaan logaritma ialah sistem yang di dalamnya memuat unsur numerus (bilangan pokok) dengan variabel atau fungsi peubah, dimana tanda yang digunakan dapat berbentuk <, >, ≤, ≥. Bentuk logaritma secara umum dapat berupa ᵃlog b = c menjadi b = aᶜ.
Baca juga : Kumpulan Rumus Perpangkatan Beserta Penjelasannya
Pada kesempatan kali ini saya akan menjelaskan tentang rumus pertidaksamaan logaritma secara lengkap. Untuk mengasah kemampuan dan pendalaman materi saya juga telah sediakan beberapa contoh soal pertidaksamaan logaritma. Oleh karenanya simaklah pembahasan di bawah hingga selesai.
Sifat Sifat Pertidaksamaan Logaritma
Bagaimana bentuk pertidaksamaan logaritma itu? Sebelum membahas tentang rumus pertidaksamaan logaritma dan contoh soal pertidaksamaan logaritma tersebut, saya akan menjelaskan terlebih dahulu mengenai sifat sifat pertidaksamaan logaritma. Pertidaksamaan logaritma memiliki beberapa sifat seperti di bawah ini:
Untuk a > 1, dimana g(x) > 0 dan f(x) > 0 yaitu:
- ᵃlog f(x) > ᵃlog g(x) → f(x) > g(x).
- ᵃlog f(x) < ᵃlog g(x) → f(x) < g(x).
- ᵃlog f(x) ≥ ᵃlog g(x) → f(x) ≥ g(x).
- ᵃlog f(x) ≤ ᵃlog g(x) → f(x) ≤ g(x).
Untuk 0 < a < 1, dimana g(x) > 0 dan f(x) > 0 yaitu:
- ᵃlog f(x) > ᵃlog g(x) → f(x) < g(x).
- ᵃlog f(x) < ᵃlog g(x) → f(x) > g(x).
- ᵃlog f(x) ≥ ᵃlog g(x) → f(x) ≤ g(x).
- ᵃlog f(x) ≤ ᵃlog g(x) → f(x) ≥ g(x).
Selain sifat sifat pertidaksamaan logaritma di atas, adapula bentuk materi pertidaksamaan logaritma di dalamnya. Bentuk bentuk pertidaksamaan ini memuat rumus pertidaksamaan logaritma dan contoh soal pertidaksamaan logaritma. Berikut penjelasan selengkapnya:
Bentuk Pertidaksamaan Logaritma I
Pertidaksamaan logaritma yang pertama memiliki bentuk ᵃlog f(x) … b. Bentuk pertidaksamaan ini dapat diubah menjadi f(x) … aᵇ. Berikut contoh soalnya:
Tentukan himpunan penyelesaian dari ²log (7x – 16) > 1?
Pembahasan.
²log (7x – 16) > 1 memiliki nilai a = 2 sehingga tanda (>) tetap atau tidak berubah. Sehingga,
²log (7x – 16) > 1
7x – 16 > 2¹
7x – 16 > 2
7x > 2 + 16
7x > 18
x > 18/7
Jadi HP = {x > 18/7}.
Baca juga : 6 Sifat Persamaan Garis Lurus dan Contoh Soalnya
Bentuk Pertidaksamaan Logaritma II
Pertidaksamaan logaritma selanjutnya memiliki bentuk ᵃlog f(x) … ᵃlog b. Bentuk ini memiliki rumus pertidaksamaan logaritma sendiri sehingga dapat diubah menjadi f(x) … b. Berikut contoh soal pertidaksamaan logaritma bentuk II yaitu:
Tentukan himpunan penyelesaian dari ³log (4x + 6) ≤ ³log 27?
Pembahasan.
³log (4x + 6) ≤ ³log 27 memiliki a = 3 sehingga tanda (≤) tetap. Maka,
³log (4x + 6) ≤ ³log 27
4x + 6 ≤ 27
4x ≤ 27 – 6
4x ≤ 21
x ≤ 21/4
Jadi HP = {x ≤ 21/4}.
Bentuk Pertidaksamaan Logaritma III
Pertidaksamaan logaritma selanjutnya memiliki bentuk ᵃlog f(x) … ᵃlog g(x). Bentuk ini memiliki rumus pertidaksamaan logaritma sendiri sehingga dapat diubah menjadi f(x) … g(x). Berikut contoh soal pertidaksamaan logaritma bentuk III yaitu:
Tentukan himpunan penyelesaian dari ⁰’⁵log (x² + x – 3) < ⁰’⁵log (x² – 3x + 12)?
Pembahasan.
⁰’⁵log (x² + x – 3) < ⁰’⁵log (x² – 3x + 12), dimana a = 0,5 (0 < a < 1) sehingga terjadi perubahan tanda (<) menjadi (>).
Maka,
⁰’⁵log (x² + x – 3) < ⁰’⁵log (x² – 3x + 12)
x² + x – 3 > x² – 3x + 12
x² + x – x² + 4x > 12 + 3
5x > 15
x > 3
Jadi HP = {x > 3}.
Demikianlah penjelasan mengenai rumus pertidaksamaan logaritma dan contoh soal pertidaksamaan logaritma. Setiap bentuk pertidaksamaan logaritma pada dasarnya menggunakan konsep sifat sifat pertidaksamaan logaritma yang sama. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi pertidaksamaan logaritma di atas.