Kumpulan Rumus Perpangkatan Beserta Penjelasannya – Jika mendengar istilah tentang “rumus” tentunya akan muncul bayangan “harus menghafal”. Hal ini dikarenakan banyak sekali persepsi salah yang menyatakan bahwa rumus tersebut ditemukan oleh orang orang hebat. Penemuan rumus ini tidak hanya berlangsung begitu saja, tetapi ada serangkaian proses yang harus dilalui sebelum rumus dijadikan sedemikian rupa. Dalam ilmu Matematika terdapat rumus yang merupakan aturan umum dalam penyelesaian masalah Matematika yang tersedia. Salah satunya ialah kumpulan rumus pangkat untuk menyelesaikan soal terkait bilangan berpangkat.
Materi bilangan berpangkat merupakan satu dari sekian materi Matematika yang perlu dipelajari. Lalu bagaimana kumpulan rumus perpangkatan itu? Kumpulan rumus pangkat ini dapat memudahkan anda untuk mengerjaan soal soal ujian terkait materi tersebut. Seperti yang telah kita ketahui bahwa rumus Matematika yang tersedia ini biasanya disertai dengan pembuktianya secara deduktif sehingga dapat berlaku secara umum dan rumus itu benar benar sah (valid).
Rumus bilangan berpangkat sering kali dianggap sulit oleh beberapa siswa. Rumus tersebut berisi operasi pembagian, perkalian, pangkat nol dan sebagainya. Bagaimana rumus pangkat itu? Pada kesempatan kali ini saya akan membahas tentang kumpulan rumus perpangkatan lengkap dengan penjelasan. Untuk lebih jelasnya dapat anda simak di bawah ini.
Kumpulan Rumus Perpangkatan Beserta Penjelasannya
Perpangkatan secara umum dapat diartikan sebagai operasi perkalian Matematika yang berulang ulang sebanyak bilangan pangkatnya. Pangkat sebuah bilangan sendiri merupakan angka yang penulisannya berada sedikit ke atas dan ukurannya lebih kecil. Penulisan pangkat menurut semantik tersebut dapat dinamakan dengan superscript. Adapun contoh bilangan berpangkat yaitu 4², 5², 6³ dan sebagainya.
Baca juga : Cara Menghitung Modus, Median, dan Mean Dari Data Tunggal
Perpangkatan dalam Bahasa Inggris dapat dinamakan dengan exponent atau power. Di bawah ini terdapat penjelasan mengenai kumpulan rumus perpangkatan yaitu sebagai berikut:
Perkalian Bilangan Berpangkat
Rumus pangkat yang pertama akan saya bahas ialah rumus perkalian pangkat. Dua bilangan berpangkat dapat dikalikan seperti di bawah in:
3³ x 3⁴
Kita dapat menguraikan masing masing pangkat ini dalam bentuk perkalian berulang hingga dapat dicari hasil akhirnya. Maka dari itu hasilnya akan seperti di bawah ini:
3³ x 3⁴ = (3 x 3 x 3) x (3 x 3 x 3 x 3)
= 27 x 81
= 2187
Berdasarkan hasil perhitungan di atas, kita dapat menemukan rumus pangkat dalam operasi perkalian yang lebih sederhana. Hasil bilangan berpangkat ini berkaitan dengan pangkat dari setiap bilangan yang dikalikan. Oleh karenanya ditemukan kumpulan rumus perpangkatan yang lebih sederhana untuk menyelesaikan perkalian ini. Untuk lebih jelasnya perhatikan pengerjaan berikut:
3³ x 3⁴ = 3³ ⁺ ⁴ = 3⁷
Hubungan yang berlaku dalam perkalian bilangan berpangkat di atas dapat terjadi apabila bilangan yang dipangkatkan sama. Dari perpangkatan di atas terdapat angka 3 yang merupakan bilangan sama yang akan dipangkatkan. Maka dari itu, kita dapat menyimpulkan bahwa rumus perkalian pangkat yang berlaku dapat seperti di bawah ini:
aᵐ × aⁿ = aᵐ ⁺ ⁿ
Rumus di atas dapat digunakan untuk pangkat dalam bilangan real
Pembagian Bilangan Berpangkat
Kumpulan rumus perpangkatan selanjutnya ditujukan untuk operasi pembagian pangkat. Untuk lebih jelasnya perhatikan contoh di bawah ini:
2⁶ / 2³ = (2 x 2 x 2 x 2 x 2 x 2) / (2 x 2 x 2)
= 2 x 2 x 2
= 2³
Baca juga : Cara Menghitung Akar Pangkat 3 Dengan Cepat dan Benar
Berdasarkan pembagian bilangan berpangkat di atas kita dapat melihat bahwa pembilang dan penyebut tersebut memiliki hubungan pangkat seperti di atas. Maka dari itu pola pembagiannya dapat dinyatakan dalam bentuk seperti di bawah ini:
2⁶ / 2³ = 2⁶ ‾ ³ = 2³
Dari hasil pengerjaan di atas dapat disimpulkan bahwa rumus pembagian pangkatnya dapat berbentuk seperti berikut:
aᵐ / aⁿ = aᵐ ‾ ⁿ
Pangkat Nol (0)
Kumpulan rumus perpangkatan selanjutnya ditujukan untuk operasi pangkat nol. Bilangan nol ialah bilangan yang cukup istimewa. Ada yang mengatakan bahwa bilangan nol ini ditemukan oleh Al-Khawarizmi. Pemerolehan bilangan nol tersebut dapat terjadi apabila bilangan yang sama dikurangkan. Oleh karena itu pemerolehan bilangan nol berasal dari hasil pengurangan dua bilangan yang sama. Berikut rumus pangkat nolnya yaitu:
a⁰ = aⁿ ‾ ⁿ = aⁿ / aⁿ = 1
Berdasarkan rumus di atas, kita dapat mengetahui bahwa bilangan apapun yang berpangkat nol pasti akan memiliki hasil berupa 1.
Pangkat Negatif
Kumpulan rumus perpangkatan selanjutnya ditujukan untuk operasi pangkat negatif. Bilangan negatif dapat diartikan sebagai invers atau kebalikan bilangan positif yang diperoleh dari operasi penjumlahan. Berikut contoh persamaannya:
n + (-n)=0 ↔ (-n) = 0 – n
Dari hasil di atas kita dapat menuliskan pangkat -n dalam bentuk 0 – n juga. Adapun rumus pangkat negatif tersebut yaitu:
aⁿ = a⁰ ‾ ⁿ = a⁰ / aⁿ = 1 / aⁿ
Kumpulan Rumus Perpangkatan Lengkap
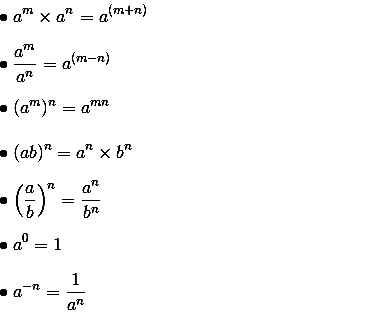
Demikianlah penjelasan mengenai kumpulan rumus perpangkatan lengkap. Perpangkatan merupakan operasi perkalian Matematika yang berulang ulang sebanyak bilangan pangkatnya. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.