Materi Pemangkatan Bentuk Aljabar (Rumus dan Contoh Soal) – Dalam Matematika pasti kita sering mendengar adanya aljabar. Apa yang dimaksud aljabar itu? Aljabar ialah sebuah cabang Matematika mengenai penyelesaian tentang masalah huruf huruf yang berguna sebagai wakil beberapa angka. Aljabar memiliki bentuk yang terdiri dari nilai tetap (konstanta), faktor pengali (koefisien) dan nilai berubah (variabel). Contohnya saja 3a + 2, dimana koefisiennya berupa 3, variabelnya berupa a dan kontantanya berupa 2. Aljabar tersebut juga termasuk dalam materi perpangkatan bentuk aljabar Matematika. Materi perpangkatan aljabar ini mencakup rumus pemangkatan aljabar dan cobtoh soal perpangkatan aljabar.

Pengertian aljabar secara umum ialah bentuk Matematika yang berguna untuk menyajikan bilangan belum diketahui, dimana diwakili oleh berbagai huruf. Biasanya penggunaan bentuk aljabar ini ialah untuk memecahkan masalah dikehidupan sehari hari. Dalam Matematika sendiri terdapat materi pemangkatan bentuk aljabar dengan rumus pemangkatan aljabar dan contoh soal perpangkatan bentuk aljabarnya sekaligus. Materi perpangkatan aljabar ini bahkan dijadikan sebagai bahan soal soal Ujian, baik Ujian Sekolah maupun Ujian Nasional.
Rumus Pangkat Bentuk Aljabar
Pada prinsipnya rumus perpangkatan bentuk aljabar memiliki persamaan dengan perpangkatan bilangan bulat. Perpangkatan disini merupakan perkalian bilangan yang sama secara berulang. Prinsip ini digunakan dalam materi pemangkatan aljabar, baik dalam rumus maupun contoh soal perpangkatan aljabar. Pada kesempatan kali ini saya akan menjelaskan tentang materi pemangkatan bentuk aljabar beserta rumus pemangkatan bentuk aljabar dan contoh soal pemangkatan bentuk aljabar. Untuk lebih jelasnya dapat anda simak di bawah ini.
Secara umum aljabar dapat diartikan sebagai bentuk Matematika yang berguna untuk menyajikan bilangan belum diketahui, dimana diwakili oleh berbagai huruf. Sedangkan perpangkatan dapat diartikan sebagai perkalian bilangan yang sama secara berulang. Secara umum perpangkatan memiliki rumus aⁿ = a x a x . . . x a, dimana a dikalikan sebanyak n. Konsep dasar ini digunakan dalam materi perpangkatan bentuk aljabar.
Baca juga : Rangkuman Materi Fungsi Kuadrat Matematika Beserta Contoh Soal
Apakah anda tahu rumus pemangkatan aljabar itu? Bagaimana cara menyelesaikan contoh soal perpangkatan bentuk aljabar itu? Dalam materi pemangkatan bentuk aljabar terdapat rumus pemangkatan aljabar yang dapat dinyatakan dalam bentuk seperti di bawah ini:
(a + b)ⁿ = (a + b) x (a + b) x (a + b) x . . . x (a + b)
Dalam rumus perpangkatan bentuk aljabar di atas terdapat (a + b) yang dikalikan sebanyak n. Sebelum membahas tentang cara menyelesaikan perpangkatan aljabar tersebut, maka saya akan menjelaskan terlebih dahulu mengenai beberapa hal yang diperhatikan dalam materi tersebut. Adapun penjelasan selengkapnya yaitu sebagai berikut:
abⁿ tidak sama dengan (ab)ⁿ
Bentuk abⁿ ini hanya memangkatkan b saja sejumlah n, sehingga a tidak ikut dipangkatkan. Tetapi untuk bentuk (ab)ⁿ terdapat pemangkatan a dan pemangkatan b sejumlah n. Misalnya:
(3a)² = (3a)(3a) = 9a²
Berbeda dengan,
3a² = 3 x a x a = 3a²
(-ab)ⁿ tidak sama dengan -(ab)ⁿ
Materi pemangkatan bentuk aljabar selanjutnya membahas tentang nilai (-ab)ⁿ yang tidak sama dengan -(ab)ⁿ. Dalam bentuk (-ab)ⁿ terdapat pemangkatan (-ab) sejumlah n. Sedangkan dalam bentuk -(ab) terdapat pemangkatan ab.
Cara Menyelesaikan Perpangkatan Bentuk Aljabar
Setelah memahami tentang rumus pemangkatan bentuk aljabar di atas. Selanjutnya saya akan menjelaskan tentang cara menyelesaikan pemangkatan aljabar. Pada dasarnya kita dapat dengan mudah bilangan aljabar yang hanya memiliki pangkat dua saja. Hal ini dikarenakan pangkat dua lebih sederhana dibandingkan pangkat lebih dari 2. Sebelum membahas lebih lanjut mengenai perpangkatan aljabar tersebut. Anda harus mengetahui konsep dasar segitiga pascal terlebih dahulu. Hal ini dikarenakan kedua hal ini saling berhubungan. Di bawah ini terdapat bentuk segitiga pascal yaitu:
Baca juga : Contoh Soal Notasi Sigma Kelas 11 Beserta Jawabannya
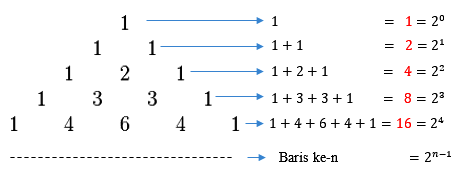
Dalam materi pemangkatan bentuk aljabar memang terdapat penerapan segitiga pascal ini. Untuk itu rumus pemangkatan aljabarnya dapat menjadi seperti di atas. Di bawah ini terdapat penggunaan segitiga pascal dalam menyelesaikan contoh soal pemangkatan aljabar yaitu sebagai berikut:
(a + b)º = 1
(a + b)¹ = a + b
(a + b)² = a² + 2ab + b²
(a + b)³ = a³ + 3a²b + 3ab² + b³
(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴
(a + b)⁵ = a⁵ + 5a⁴b + 10a³b² + 10 a²b³ + 5ab⁴ + b⁵
Contoh Soal Pemangkatan Aljabar
Setelah menjelaskan tentang rumus perpangkatan bentuk aljabar dalam materi pemangkatan bentuk aljabar di atas. Selanjutnya saya akan membagikan beberapa contoh soal perpangkatan aljabar terkait rumus pemangkatan aljabar tersebut. Adapun contoh soal dan pembahasannya yaitu sebagai berikut:
Tentukan hasil perpangkatan bilangan di bawah ini:
1. (-4a)²
2. -(2b)³
3. (3xy)²
Jawab.
1. (-4a)² = (-4a) x (-4a) = 16a²
2. -(2b)³ = -{(2b)(2b)(2b)} = -8b³
3. (3xy)² = (3xy)(3xy) = 9x²y²
Untuk menyelesaikan masalah pemangkatan aljabar tersebut dapat memahami beberapa tips seperti di bawah ini:
- Langkah pertama ialah mengetahui bentuk perpangkatan dan memahaminya.
- Lalu pola segitiga pascalnya dipahami dalam bentuk (a + b)ⁿ.
- Perpangkatan bentuk aljabar tersebut disubstitusikan ke pola segitiga pascal.
Sekian penjelasan mengenai materi pemangkatan bentuk aljabar beserta rumus pemangkatan bentuk aljabar dan contoh soal pemangkatan bentuk aljabar. Untuk menyelesaikan masalah perpangkatan bentuk aljabar pada umumnya menggunakan konsep segitiga pascal. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.