Contoh Soal Dilatasi Beserta Pengertian dan Rumus Lengkap – Materi transformasi merupakan salah satu materi dalam Matematika. Transformasi sendiri dapat didefinisikan sebagai perubahan. Untuk itu pengertian transformasi geometri ialah sebuah objek yang mengalami perpindahan di area geometri. Materi transformasi geometri ini telah diajarkan ketika di bangku Sekolah Menengah Atas Kelas XII. Menariknya, contoh soal dilatasi masuk dalam pembahasan materi tersebut. Selain rumus dilatasi, siswa juga dituntut untuk menghafal pengertian serta aspek lainnya.
Apa yang dimaksud dilatasi? Pengertian dilatasi ialah jenis transformasi geometri yang berbentuk perkalian. Dimana fungsinya untuk mengurangi ataupun memperbesar bangunan pada geometri. Dilatasi ini dapat dinamakan dengan pelebaran. Pelebaran tersebut dapat memuat faktor dilatasi maupun titik pelebaran. Bagaimana cara menyelesaikan contoh soal dilatasi itu? Cara menghitung dilatasi tersebut dapat dilakukan dengan menggunakan rumus dilatasi yang tersedia. Dalam materi dilatasi terdapat titik dilatasi yang merupakan titik untuk mencari posisi pada dilatasi. Hasil titik dilatasi dapat berbentuk titik titik yang dihubungkan dalam titik pertemuan antara garis garis lurus yang tersedia.
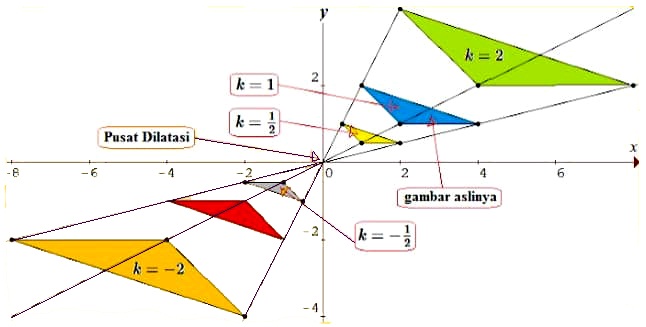
Dalam materi ini juga terdapat faktor dilatasi yang merupakan faktor pada struktur geometri yang berbentuk multiplikasi dilatasi. Faktor tersebut memiliki simbol k dan digunakan untuk mencari hasil dari besarnya perluasan geometri. Pelebaran ini memiliki hasil yang lebih besar dibandingkan geometri dengan bentuk nilai k < -1 atau k > -1. Jika pelebaran memiliki hasil yang lebih kecil dibandingkan geometri, maka memiliki nilai -1 < k < 1. Pada kesempatan kali ini saya akan membagikan contoh soal dilatasi beserta pengertian dilatasi dan rumus dilatasi lengkap. Untuk lebih jelasnya dapat anda simak di bawah ini.
Contoh Soal Dilatasi Beserta Pengertian dan Rumus Lengkap
Jika dalam satu sisi pada titik dilatasi terdapat hasil dilatasi dengan geometri saling berdampingan, maka tandanya pasti positif. Sedangkan jika pada titik dilatasi berbeda terdapat hasil pelebaran dibalik sisi dan geometri tidak berdampingan, maka tandanya pasti negatif. Penulisan dilatasi dapat berupa (D, k), dimana D = titik dilatasi dan k = faktor dilatasi. Dilatasi dalam Matematika dapat dinamakan dengan perkalian atau pembesaran. Pengertian dilatasi secara umum ialah sebuah transformasi pada sebuah bangun untuk diubah ukurannya menjadi lebih besar atau lebih kecil, namun bentuk bangun yang berhubungan tidak diubah.
Baca juga : Contoh Soal Translasi (Pergeseran) Beserta Pembahasannya
Fakor dilatasi atau faktor skala dan titik pusat dapat digunakan untuk mencari dilatasi. Dilatasi dapat dinotasikan dalam faktor skala berbentuk [O, k] dan titik pusat O(0,0). Berdasarkan pengertian diatasi tersebut, kita tahu bahwa dilatasi tersebut digunakan untuk memperbesar dan memperkecil sebuah bangun geometri. Untuk menentukan nilai dilatasi ini dapat menggunakan rumus dilatasi yang tersedia. Sebelum membagikan contoh soal dilatasi tersebut, saya akan menjelaskan sifat sifat dilatasi terlebih dahulu. Dilatasi memiliki beberapa sifat seperti di bawah ini:
Sifat Sifat Dilatasi
Dilatasi digunakan untuk mengubah faktor pengali dengan jarak titik yang terdapat pada sebuah titik tertentu. Faktor pengali ini dapat dinamakan dengan faktor skala atau faktor dilatasi. Sedangkan titik tertentu ini dapat disebut sebagai pusat dilatasi. Untuk itu dilatasi dapat dipengaruhi oleh pusat dilatasi dan faktor dilatasi. Untuk itu notasi dilatasi berdasarkan faktor skala dan berpusat di P dapat berbentuk seperti di bawah ini:
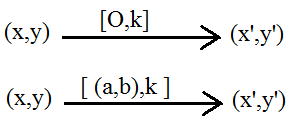
Sebelum membagikan contoh soal dilatasi, saya akan membagikan beberapa sifat dari dilatasi. Dilatasi tersebut memiliki beberapa sifat seperti di bawah ini:
- Apabila bangun semula dan pusat dilatasi dengan bangun bayangannya memiliki letak sepihak dan diperbesar, maka nilai k > 1.
- Apabila bangun semula dan pusat dilatasi dengan bangun bayangannya memiliki letak sepihak dan diperkecil, maka nilainya 0 < k < 1.
- Apabila bangun semula dan pusat dilatasi dengan bangun bayangannya memiliki letak tidak sepihak dan diperkecil, maka nilainya -1 < k < 0.
- Apabila bangun semula dan pusat dilatasi dengan bangun bayangannya memiliki letak tidak sepihak dan diperbesar, maka nilainya k < -1.
Baca juga : Kumpulan Soal Barisan dan Deret Aritmatika Beserta Pembahasan
Dari sifat sifat dilatasi tersebut dapat diketahui bahwa titik pusat (0,0) [O,k] dapat berhubungan dengan materi dilatasi ini. Bayangan (x’,y’) pada umumnya dapat ditentukan dari titik asal (x,y) menggunakan rumus dilatasi seperti di bawah ini:
x’ = kx dan y’ = ky
k dalam rumus tersebut merupakan perbesaran objek dilatasi atau faktor dilatasi. Benda yang diperbesar memiliki nilai |k| > 1, sedangkan benda yang diperkecil memiliki nilai 0 < |k| < 1.
Contoh Soal Dilatasi
Setelah menjelaskan tentang pengertian dilatasi, rumus dilatasi dan sifat sifat dilatasi di atas. Selanjutnya saya akan membagikan contoh soal beserta cara menghitung dilatasi. Berikut contoh soal dan pembahasannya:
Peta kurva memiliki persamaan berupa y = x² – 6x + 5. Kemudian dilanjutkan dengan dilatasi karena pencerminan dilakukan pada sumbu x dengan faktor skala 3 dan pusat. Tentukan persamaan baru yang dibentuk oleh dilatasi tersebut?
Pembahasan.
Persamaan pada sumbu x memiliki bentuk seperti di bawah ini:
P(x,y) → P'(x,-y)
Untuk itu dilatasi yang melalui faktor skala 3 dan titik pusat O(0,0) dapat dibentuk dari proses seperti di bawah ini:
[O, k] : P(x,y) → P'(kx, ky)
[O,3k] : P(x,y) → P'(3x, 3y)
Setelah itu dilatasi melabjutkan pencermina pada titik pusat O(0,0) dengan skala 3 dan pusat O dengan persamaan seperti berikut:
P(x,y) → P'(x, -y) → P”(3x, -3y)
Sehingga:
x” = 3x → x = 1/3 x”
y” = 3y → y = 1/3 y”
Kemudian nilainya disubstitusikan ke persamaan y = x² – 6x + 5, maka hasilnya menjadi:
y = y² – 4x + 3
1/3 y” = (1/3 x”)² – 6(1/3x”) + 5
1/3 y” = 1/9 x”² – 2x” + 5 → x 9
3y” = 3x”² – 18x” + 45
3y” – 3x”² + 18x” – 45 = 0
Jadi persamaannya akan menjadi 3y – 3x² + 18x – 45 = 0.
Inilah penjelasan mengenai contoh soal dilatasi beserta pengertian dilatasi dan rumus dilatasi lengkap. Dilatasi merupakan sebuah transformasi pada sebuah bangun untuk diubah ukurannya menjadi lebih besar atau lebih kecil, namun bentuk bangun yang berhubungan tidak diubah. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi dilatasi di atas.


