Mencari Himpunan Penyelesaian Pertidaksamaan – Dalam ilmu Matematika terdapat materi pembelajaran mengenai pertidaksamaan. Apa itu pertidaksamaan Matematika? Pertidaksamaan sendiri memiliki pengertian yaitu pernyataan atau kalimat dalam Matematika yang menggambarkan ukuran perbandingan dua objek atau lebih. Pertidaksamaan Matematika ini memiliki beberapa notasi dasar seperti < (kurang dari), > (lebih dari), ≤ (kurang dari sama dengan), ≥ (lebih dari sama dengan), dan ≠ (tidak sama dengan).
Secara umum tanda tanda dalam notasi dasar dapat digunakan untuk mencari himpunan penyelesaikan pertidaksamaan. Materi himpunan penyelesaian pertidaksamaan ini sebenarnya telah dipelajari ketika di bangku sekolah. Bahkan dalam materi ini juga sering muncul dalam soal soal ujian Matematika, baik ujian sekolah maupun ujian Nasional.
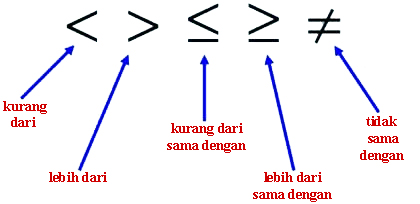 |
| Notasi Pertidaksamaan |
Himpunan pertidaksamaan Matematika dapat dibagi menjadi beberapa jenis. Setiap jenis memiliki cara penyelesaian pertidaksamaan yang berbeda beda. Maka dari itu langkah langkah mencari himpunan penyelesaian dalam pertidaksamaannya juga berbeda beda. Nah dalam pembahasan kali ini saya akan menjelaskan tentang cara mencari himpunan penyelesaian pertidaksamaan. Untuk lebih jelasnya dapat anda simak di bawah ini.
Mencari Himpunan Penyelesaian Pertidaksam
aan
Seperti yang sudah saya jelaskan di atas bahwa pertidaksamaan Matematika dapat dibagi menjadi beberapa jenis. Jenis jenis himpunan pertidaksamaan Matematika tersebut meliputi pertidaksamaan linear, pertidaksamaan mutlak, pertidaksamaan pecahan, pertidaksamaan kuadrat, pertidaksamaan bentuk akar dan pertidaksamaan pangkat tinggi.
Setiap jenis himpunan memiliki penyelesaian pertidaksamaan yang berbeda beda, meskipun tanda/notasi dasar yang digunakan tersebut sama (<, >, ≤, ≥, ≠). Berikut penjelasan mengenai cara mencari himpunan penyelesaian pertidaksamaannya:
Baca juga : Rumus dan Contoh Pertidaksamaan Linear Satu Variabel
Pertidaksaman Linear
Jenis pertidaksamaan Matematika yang pertama ialah pertidaksamaan linear. Pertidaksamaan linear ialah kalimat terbuka yang memiliki variabel dengan pangkat tertingginya 1 (bilangan bulat positif) serta menggunakan tanda <, >, ≤, atau ≥. Cara menghitung himpunan penyelesaian pertidaksamaan ini tergantung pada bentuk linearnya. Adapun beberapa bentuk umum pertidaksamaan linear yaitu meliputi:
ax + b < c
ax + b > c
ax + b ≤ c
ax + b ≥ c
Keterangan :
x = Variabel
a = Koefisien
b dan c = Konstanta
Selain itu pertidaksamaan linear juga dapat dinyatakan dalam bentuk garis bilangan. Untuk lebih jelasnya dapat anda simak contoh di bawah ini.
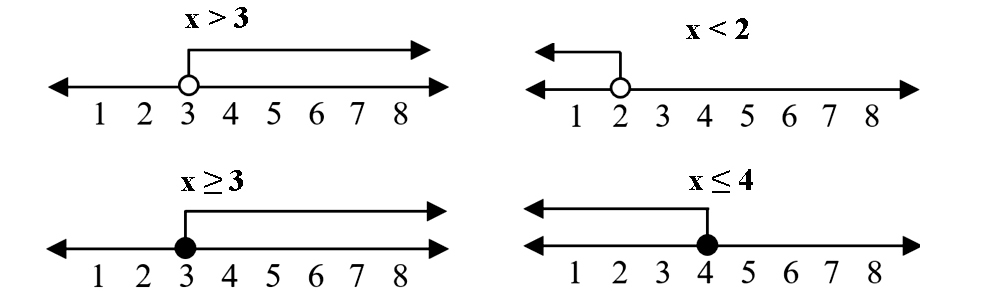 |
| Contoh Bentuk Garis Bilangan Pertidaksamaan Linear |
Lalu bagaimana cara mencari pertidaksamaan linearnya? Himpunan penyelesaian pertidaksamaan linear dapat dicari dengan memisahkan variabel pada ruas tersendiri agar terpisah dengan konstantanya
Pertidaksamaan Kuadrat
Jenis pertidaksamaan Matematika selanjutnya ialah pertidaksamaan kuadrat. Pertidaksamaan kuadrat ialah himpunan pertidaksamaan yang memiliki variabel dengan pangkat tertingginya 2 (bilangan bulat positif) serta menggunakan tanda <, >, ≤, atau ≥. Cara mencari himpunan penyelesaian pertidaksamaan ini tergantung pada bentuk kuadratnya. Adapun beberapa bentuk umum pertidaksamaan kuadrat yaitu meliputi:
ax² + bx + c < 0
ax² + bx + c > 0
ax² + bx + c ≤ 0
ax² + bx + c ≥ 0
dimana a ≠ 0, serta a, b, c ϵ R
Di bawah ini terdapat langkah langkah menentukan himpunan penyelesaian pertidaksamaan kuadrat. Berikut penjelasan selengkapnya:
- Langkah pertama yaitu memindahkan semua suku menjadi satu ruas saja. Dengan begitu terdapat salah satu ruas yang kosong. Nah hasilnya akan menjadi ruang kiri berisi semua suku dan ruas kanan kosong.
- Kemudian bentuk kuadrat di ruas kiri diselesaikan menggunakan cara pemfaktoran. Dengan begitu akan terlihat hasilnya sehingga dapat mempemudah anda menyelesaikan pertidaksamaan kuadrat tersebut.
- Selanjutnya ialah membentuk himpunan penyelesaian pertidaksamaan dalam garis bilangan. Dengan begitu nilai garis bilangan itu akan dijadikan pembatas interval pada himpunan pertidaksamaan tadi.
Baca juga : Pembahasan Soal Deret Angka Dalam Tes Psikotes
Pertidaksamaan Pangkat Tinggi
Jenis pertidaksamaan Matematika selanjutnya ialah pertidaksamaan pangkat tinggi. Pertidaksamaan pangkat tinggi ialah himpunan pertidaksamaan yang memiliki variabel dengan pangkat lebih dari 2 (bilangan bulat positif) serta menggunakan tanda <, >, ≤, atau ≥. Cara mencari himpunan penyelesaian pertidaksamaan ini tergantung pada bentuk pangkat tingginya. Adapun beberapa bentuk pertidaksamaan pangkat tinggi yaitu meliputi:
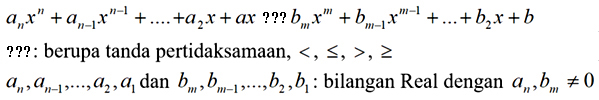 |
| Bentuk Umum Petidaksamaan Pangkat Tinggi |
Di bawah ini terdapat langkah langkah menentukan himpunan penyelesaian pertidaksamaan pangkat tinggi. Berikut penjelasan selengkapnya:
- Langkah pertama yaitu memindahkan semua suku menjadi satu ruas saja. Dengan begitu terdapat salah satu ruas yang kosong. Nah hasilnya akan menjadi ruang kiri berisi semua suku dan ruas kanan kosong.
- Selanjutnya ialah bentuk pangkat tinggi tersebut disederhanakan menjadi pangkat yang lebih rendah dengan cara pemfaktoran. Dengan begitu akan lebih mudah dalam mencari nilai pertidaksamaannya.
- Setelah hasil nilai ditemukan, kemudian buat menjadi bentuk garis bilangan dan tentukan daerah bilangan menggunakan tanda pertidaksamaannya.
Pertidaksamaan Pecahan
Jenis pertidaksamaan Matematika selanjutnya ialah pertidaksamaan pecahan. Pertidaksamaan pecahan ialah pertidaksamaan yang memiliki fungsi pecahan serta menggunakan tanda <, >, ≤, atau ≥. Cara mencari himpunan penyelesaian pertidaksamaan ini tergantung pada bentuk pecahannya. Adapun beberapa bentuk pertidaksamaan pecahan yaitu meliputi:
 |
| Bentuk Umum Pertidaksamaan Pecahan |
Di bawah ini terdapat langkah langkah menentukan himpunan penyelesaian pertidaksamaan pecahan. Berikut penjelasan selengkapnya:
- Langkah pertama yaitu memindahkan semua suku menjadi satu ruas saja. Dengan begitu terdapat salah satu ruas yang kosong. Nah hasilnya akan menjadi ruang kiri berisi semua suku dan ruas kanan kosong. Dalam pertidaksamaan ini tidak dianjurkan untuk menggunakan proses perkalian silang. Hal ini dikarenakan bentuk pertidaksamaannya akan berubah dan tidak sesuai.
- Selanjutnya ubah bentuk pecahan tersebut menjadi bentuk yang sederhana menggunakan operasi aljabar. Setelah itu cari nilai x dengan menggunakan pemfaktoran.
- Setelah hasil nilai ditemukan, kemudian buat menjadi bentuk garis bilangan dan tentukan daerah bilangan menggunakan tanda pertidaksamaannya.
Baca juga : 10 Jenis Pola Bilangan Beserta Rumus dan Contohnya
Pertidaksamaan Bentuk Akar
Jenis pertidaksamaan Matematika selanjutnya ialah pertidaksamaan bentuk akar. Pertidaksamaan bentuk akar ialah pertidaksamaan yang melibatkan fungsi dalam akar serta menggunakan tanda <, >, ≤, atau ≥. Cara mencari himpunan penyelesaian pertidaksamaan ini tergantung pada bentuk akarnya. Adapun beberapa bentuk pertidaksamaan bentuk akar yaitu meliputi:
 |
| Bentuk Umum Pertidaksamaan Bentuk Akar |
Di bawah ini terdapat langkah langkah menentukan himpunan penyelesaian pertidaksamaan bentuk akar. Berikut penjelasan selengkapnya yaitu:
- Cara menyelesaikan pertidaksamaan ini dapat dilakukan dengan mengkuadratkan kedua ruasnya.
- Kemudian mengecek syarat penyelesaian akarnya agar nilainya bersifat positif ataupun sama dengan nol. Hal ini berlaku untuk semua konstanta pada ruas lain.
Pertidaksamaan Mutlak
Kemudian yang terakhir ialah cara mencari himpunan penyelesaian pertidaksamaan mutlak. Pertidaksamaan ini memiliki aturan khusus dalam mencari himpunan penyelesaiannya. Adapun aturan khusus pertidaksamaan mutlak yaitu sebagai berikut:
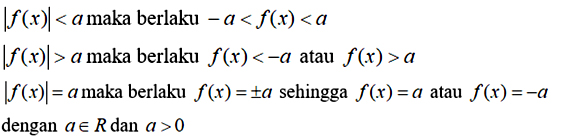 |
| Aturan Khusus Pertidaksamaan Mutlak |
Biasanya cara menentukan himpunan penyelesaian pertidaksamaan mutlak selalu dikaitkan dengan pertidaksamaan lainnya. Namun semua itu tidak terlepas dari aturan khusus di atas.
Sekian penjelasan mengenai cara mencari himpunan penyelesaian pertidaksamaan. Pertidaksamaan Matematika ini dapat dibagi menjadi beberapa jenis seperti pertidaksamaan linear, pertidaksamaan mutlak, pertidaksamaan pecahan, pertidaksamaan kuadrat, pertidaksamaan bentuk akar dan pertidaksamaan pangkat tinggi. Semoga artikel ini dapat bermanfaat dan dapat menambah wawasan anda.


