Contoh Soal Bangun Datar Gabungan Beserta Pembahasannya – Pengertian bangun datar secara umum ialah bangun dua dimensi yang memiliki garis lengkung ataupun garis lurus sebagai pembatasnya. Selain itu bangun datar juga memiliki luas maupun keliling. Bangun datar pada dasarnya dapat dibagi menjadi beberapa jenis. Setiap jenis bangun datar memiliki bentuk yang berbeda beda. Adapun macam macam bangun datar yaitu seperti persegi, jajar genjang, belah ketupat, lingkaran, segitiga, layang layang, persegi panjang dan jajar genjang. Kemudian beberapa bangun datar ini dapat dijadikan menjadi satu sehingga menggabung menjadi satu kesatuan. Lalu bagaimana cara menghitung bangun datar gabungan itu? Bagaimana rumus bangun datar gabungan itu?
Untuk menyelesaikan contoh soal bangun datar gabungan ini pada umumnya dapat menggunakan rumus bangun datar itu sendiri. Kemudian baru menghitung persoalan apa yang ingin ditentukan. Bangun datar ini memang merupakan nama sebutan dari bangun dua dimensi. Biasanya untuk materi bangun datar gabungan tersebut berisi soal soal terkait luas dan keliling yang dicari. Maka dari itu luas dari gabungan dua bangun datar atau lebih dapat disebut sebagai luas gabungan bangun datar. Sedangkan keliling dari gabungan dua bangun datar atau lebih ini dapat disebut keliling gabungan bangun datar.
Anda harus memahami terlebih dahulu cara menghitung luas dan keliling bangun datar yang menyusun bangun datar gabungan tersebut agar dapat menyelesaikan soal soalnya. Setelah masing masing bangun datar diketahui rumusnya, maka anda dapat langsung menerapkannya pada soal. Rumus bangun datar gabungan ini dapat berupa rumus luas bangun datar maupun rumus keliling bangun datar. Nah pada kesempatan kali ini saya akan membagikan contoh soal bangun datar gabungan beserta pembahasannya. Untuk lebih jelasnya dapat anda simak di bawah ini.
Contoh Soal Bangun Datar Gabungan Beserta Pembahasannya
Untuk menyelesaikan contoh soal gabungan bangun datar ini dapat dilakukan dengan mengenali masing masing bangun datar tersebut. Hal ini bertujuan untuk mengetahui jenis rumus bangun datar gabungan yang akan digunakan, baik rumus luas ataupun rumus keliling. Kemudian bangun bangun datar yang digabung tadi dipisah agar dapat berdiri sendiri. Hal ini dilakukan agar setiap bangun datarnya dapat dicari luas dengan mudah. Langkah berikutnya ialah mencari ukuran dari masing masing bangun datar, karena terkadang salah satu ukurannya memang sengaja di sembunyikan atau tidak di tulis dalam soal.
Baca juga : Contoh Soal Bangun Datar Jenjang SD Beserta Pembahasannya
Setelah mencari bagian bagian yang disembunyikan, kemudian tinggal mencari luas atau keliling dari bangun datar gabungan tersebut. Anda dpat menerapkan rumus luas bangun datar maupun rumus keliling bangun datar yang tersedia. Di bawah ini terdapat beberapa contoh soal bangun datar gabungan beserta pembahasannya yaitu sebagai berikut:
1. Perhatikan gambar di bawah ini!
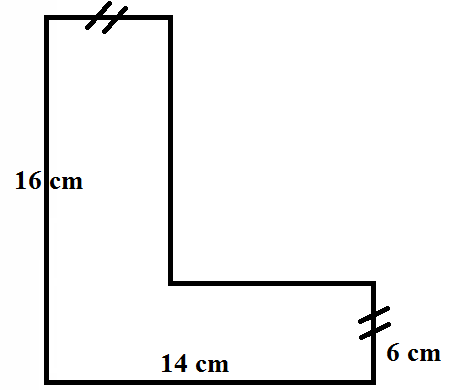
Hitunglah keliling dari bangun di atas?
Pembahasan.
Langkah pertama ialah melengkapi ukuran ukuran dari bangun tersebut, Maka hasil gambarnya akan menjadi seperti berikut setelah ukurannya dilengkapi: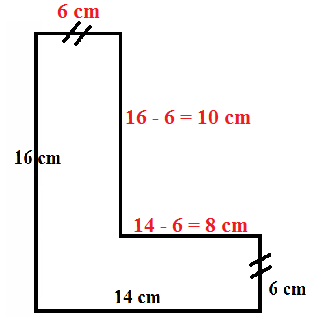
Keliling ialah jumlah garis garis pada sebuah bangun yang digunakan untuk membatasinya. Untuk itu hasilnya akan menjadi seperti di bawah ini:
Keliling = 16 + 14 + 6 + 8 + 10 + 6 = 60 cm
Jadi keliling bangun datar gabungan tersebut ialah 60 cm.
2. Perhatikan gambar di bawah ini!
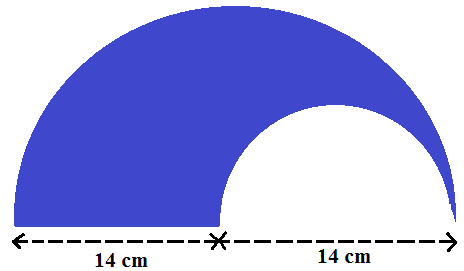
Tentukan luas bangun di atas?
Baca juga : Rumus Perbandingan Berbalik Nilai Beserta Contoh Soalnya
Pembahasan.
Contoh soal bangun datar gabungan tersebut merupakan dua buah lingkaran yang di gabung menjadi satu. Untuk menyelesaikan contoh soal tersebut dapat menggunakan rumus bangun datar gabungan berupa rumus luas lingkaran. Adapun caranya yaitu:
Luas lingkaran I = ½ luas lingkaran besar
= ½ x л x r x r
= ½ x 22/7 x 14 x 14
= 308 cm²
Luas lingkaran II = ½ luas lingkaran kecil
= ½ x л x r x r
= ½ x 22/7 x 7 x 7
= 77 cm²
Luas bangun = Luas lingkaran I – Luas lingkaran II
= 308 cm² – 77 cm²
= 231 cm²
Jadi luas bangun datar gabungan tersebut ialah 231 cm².
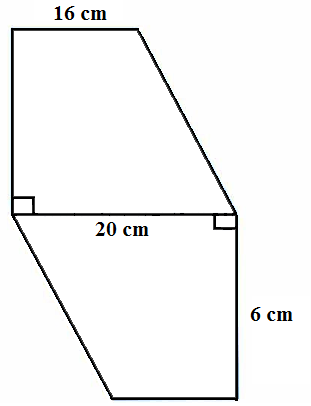
3. Tentukan luas bangun datar gabungan di bawah ini!
Pembahasan.
Contoh soal bangun datar gabungan tersebut merupakan dua buah trapesium siku siku yang di gabung menjadi satu. Untuk menyelesaikan contoh soal tersebut dapat menggunakan rumus bangun datar gabungan berupa rumus luas trapesium. Adapun caranya yaitu:
Luas Trapesium I = ½ x (a + b) x t
= ½ x (16 + 20) x 6
= 108 cm²
Luas Trapesium II = Luas Trapesium I = 108 cm²
Luas bangun seluruhnya = 2 x 108 cm²
= 216 cm²
Jadi luas bangun tersebut ialah 216 cm².
4. Perhatikan gambar di bawah ini!
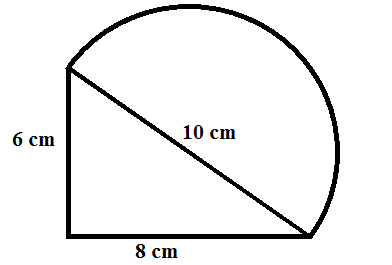
Tentukan luas bangun di atas?
Pembahasan.
Contoh soal bangun datar gabungan tersebut merupakan bangun segitiga dan lingkaran yang di gabung menjadi satu. Untuk menyelesaikan contoh soal tersebut dapat menggunakan rumus bangun datar gabungan berupa rumus luas segitiga dan rumus luas lingkaran. Adapun caranya yaitu:
alas segitiga (a) = 8 cm
tinggi segitiga (t) = 6 cm
jari jari lingkaran (r) = 10 : 5 = 5 cm
Baca juga : Pengertian Titik, Garis, Bidang dan Ruang Terlengkap
Luas segitiga = ½ x a x t
= ½ x 8 x 6
= 24 cm²
Luas ½ Lingkaran = ½ x л x r x r
= ½ x 3,14 x 5 x 5
= 39,25 cm²
Luas seluruhnya = Luas segitiga + Luas ½ Lingkaran
= 24 cm² + 39,25 cm²
= 63,25 cm²
Jadi luas bangun tersebut ialah 63,25 cm².
5. Tentukan luas daerah yang diarsir pada bangun di bawah ini?
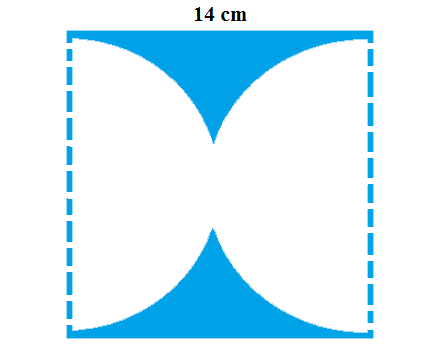
Pembahasan.
Contoh soal bangun datar gabungan tersebut merupakan bangun persegi dan lingkaran yang di gabung menjadi satu. Untuk menyelesaikan contoh soal tersebut dapat menggunakan rumus bangun datar gabungan berupa rumus luas persegi dan rumus luas lingkaran. Adapun caranya yaitu:
Sisi persegi (s) = 14 cm
Jari jari lingkaran (r) = 14 : 2 = 7 cm
Luas Persegi = s x s
= 14 x 14
= 196 cm²
Luas lingkaran = л x r x r
= 22/7 x 7 x 7
= 154 cm²
Luas daerah yan diarsir = Luas persegi – Luas lingkaran
= 196 cm² – 154 cm²
= 42 cm²
Jadi luas daerah yang diarsir pada bangun tersebut ialah 42 cm².
Demikianlah contoh soal bangun datar gabungan beserta pembahasannya yang dapat saya bagikan. Pengertian bangun datar gabungan ialah bangun yang terdiri dari dua bangun datar atau lebih dan memiliki garis lengkung ataupun garis lurus sebagai pembatasnya. Semoga artikel ini dapat bermanfaat dan terima kasih telah membaca materi bangun datar gabungan di atas.