Hubungan Antar Garis Kelas 4 SD Semester 2 dan Contoh Soalnya Terlengkap – Dalam ilmu Matematika kelas 4 SD semester 2 terdapat pembahasan mengenai hubungan antara dua garis. Materi ini dihubungkan dengan pembentukan sudut dan penjelasan mengenai dua garis yang berpotongan dalam suatu garis. Hubungan dua garis ini dapat berupa sejajar, bersilangan, berpotongan dan berimpit. Selain itu adapula materi pembentukan sudut berasal dari dua garis sejajar yang berpotongan dalam suatu garis sehingga saling bertolak belakang, luar berseberangan, luar sepihak, sudut sehadap, dalam berseberangan, dan sepihak. Perpotongan dua garis dapat membentuk sudut tertentu. Besar sudut ini dapat dihitung apabila besar salah satu sudutnya diketahui. Kemudian besar sudutnya dicari menggunakan konsep hubungan antara garis garis tersebut.
Seperti yang telah saya katakan bahwa hubungan antar garis kelas 4 SD mencakup beberapa hal di dalamnya. Contohnya perpotongan dua garis sejajar akan membentuk sudut, dimana besarnya dapat dicari apabila dalam suatu garis terdapat besar salah satu sudut yang diketahui. Lalu bagaimana cara mencari besar sudut pada hubungan antara dua garis itu? Pada umumnya materi hubungan dua garis kelas 4 SD telah diajarkan di bangku sekolah. Materi materi ini juga sering digunakan sebagai bahan soal soal Ujian, baik Ujian Nasional ataupun Ujian Sekolah. Untuk itulah para siswa diharapkan memahami hubungan pada dua garis beserta pembentukan sudut karena hubungan tersebut.
Dalam kompetensi dasar (KD) kelas 4 SD pada umumnya terdapat pembahasan mengenai materi hubungan dua garis. Materi ini tercantum dalam pembelajaran Matematika. Biasanya hubungan antara dua garis akan digabungkan dengan sudut yang terbentuk karena hubungan ini. Kompetensi dasar (KD) Matematika kelas 4 SD semester 2 ini digunakan untuk bahan penilaian harian untuk siswa. Materi tersebut dijelaskan dalam bentuk model konkret, baik hubungan garis yang berhimpit, sejajar ataupun berpotongan. Pada kesempatan kali ini saya akan menjelaskan tentang hubungan antar garis kelas 4 SD semester 2 dan contoh soalnya terlengkap. Untuk lebih jelasnya dapat anda simak di bawah ini.
Hubungan Antar Garis Kelas 4 SD Semester 2 dan Contoh Soalnya Terlengkap
Pengertian garis ialah titik titik yang dikumpulkan sampai jumlahnya tidak terhingga, dimana memanjang menuju dua arah dan saling bersebelahan. Seperti yang telah saya katakan di atas bahwa hubungan dua garis terdiri dari berpotongan, bersilangan, sejajar dan berimpit. Hubungan tersebut akan membentuk sudut tertentu yang besarnya berbeda beda. Bagaimana cara menyelesaikan contoh soal hubungan antara dua garis itu? Berapa besar sudut yang dibentuk oleh perpotongan garis tersebut?
Baca juga : Materi Limit Fungsi Aljabar Beserta Rumus dan Contoh Soalnya
Sudut yang terbentuk dari hubungan dua garis memiliki besar yang berbeda beda. Besar sudut tersebut digunakan sebagai dasar penamaan sudut sudutnya. Garis garis yang berpotongan akan menggambarkan adanya hubungan tertentu. Di bawah ini terdapat beberapa macam hubungan antar garis kelas 4 SD semester 2 beserta contoh soalnya yaitu sebagai berikut:
Berimpit
Hubungan antara dua garis yang pertama ialah berimpit. Kedua garis dinyatakan memiliki hubungan berimpit apabila letak semua titik pada suatu garis berada di garis lainnya. Di bawah ini terdapat gambar hubungan dua garis berimpit yaitu sebagai berikut:
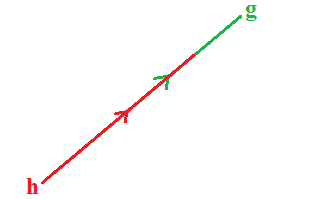
Sejajar
Hubungan antara dua garis selanjutnya ialah sejajar. Dua garis dikatakan sejajar apabila letak kedua garis tidak memiliki titik potong atau titik persekutuan dalam satu bidang datar. Kedua garis tersebut tidak akan saling bertemu meskipun diperpanjang sejauh mungkin. Adapun contoh dua garis dikatakan sejajar yaitu sebagai berikut:
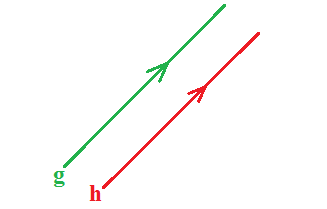
Berpotongan
Hubungan antar garis kelas 4 SD selanjutnya ialah berpotongan. Apabila dua garis memiliki satu titik potong atau titik persekutuan, maka dapat dinyatakan sebagai dua garis berpotongan. Untuk lebih jelasnya dapat anda simak dua garis berpotongan yaitu sebagai berikut:
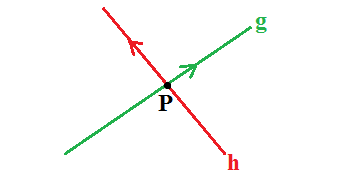
Bersilangan
Hubungan dua garis selanjutnya ialah bersilangan. Apabila dalam bidang berbeda terdapat dua garis yang tidak berpotongan dan tidak sejajar, maka dapat dikatakan bahwa dua garis bersilangan. Adapun contoh gambar dua garis bersilangan yaitu sebagai berikut:
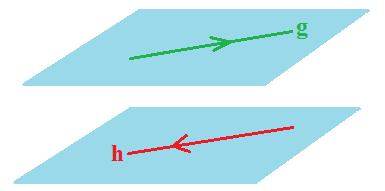
Baca juga : Rumus Perkalian Matriks dan Perkalian Skalar Matriks Lengkap
Jenis Sudut dari Perpotongan Dua Garis
Setelah menjelaskan tentang hubungan antar garis kelas 4 SD semester 2 di atas. Kemudian saya akan membagikan beberapa macam sudut karena perpotongan dua garis. Dua garis yang saling berpotongan akan membentuk beberapa jenis sudut. Pengertian sudut sendiri ialah daerah bertemunya dua sinar garis yang dibatasi pada satu titik pangkal. Untuk lebih jelasnya dapat anda perhatikan gambar di bawah ini:
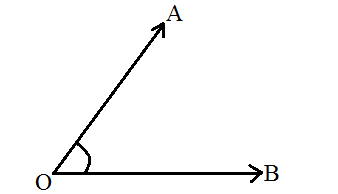
Keterangan:
O = Titik pangkal
OB dan OA = Kaki sudut
∠AOB = Daerah sudut
Jenis jenis sudut menurut besar sudutnya dapat dibagi menjadi beberapa macam seperti sudut lancip, sudut tumpul, sudut refleks, sudut lurus dan sudut siku siku. Jenis jenis sudut ini tentunya berhubungan dengan materi hubungan antara dua garis tersebut. Di bawah ini terdapat gambar gambar sudut menurut besar sudutnya yaitu sebagai berikut:
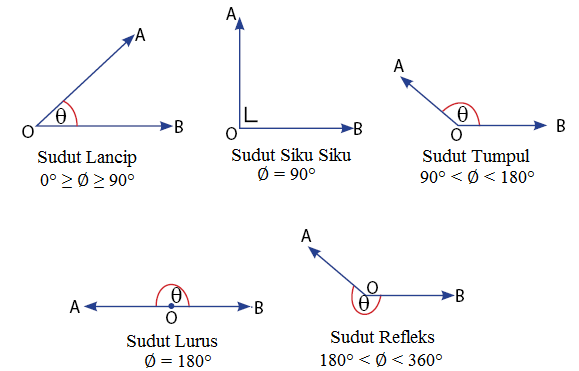
Sudut yang Terbentuk dari Sebuah Garis Memotong Dua Garis Sejajar
Dalam materi hubungan antar garis kelas 4 SD juga mencakup penjelasan mengenai pembentukan sudut karena sebuah garis memotong dua garis sejajar. Misalnya garis g sejajar dengan garis h dimana terdapat sebuah garis yang memotongnya, namun garis tersebut tidak sejajar dengan garis g dan h. Garis garis yang berpotongan tadi akan menghasilkan sudut baru seperti sudut bertolak belakang, sudut luar berseberangan, luar sepihak, sehadap, dalam berseberangan dan sepihak. Berikut penjelasan selengkapnya:
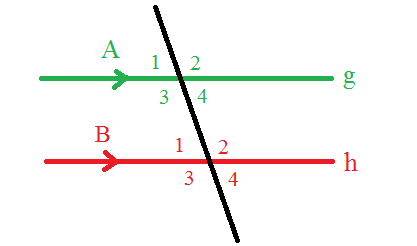
Sudut Sehadap
Sudut sehadap merupakan salah satu sudut yang terbentuk karena dua garis sejajar dipotong oleh sebuah garis lain yang tidak sejajar. Sudut sehadap ini memiliki karakteristik yaitu besar sudut yang dimiliki itu sama. Adapun beberapa sudut yang memiliki karakteristik sehadap yaitu sebagai berikut:
∠A1 = ∠B1
∠A2 = ∠B2
∠A3 = ∠B3
∠A4 = ∠B4
Baca juga : Kumpulan Soal Logaritma Beserta Jawabannya Lengkap
Sudut Dalam Beseberangan
Sudut dalam berseberangan merupakan salah satu sudut yang terbentuk karena dua garis sejajar dipotong oleh sebuah garis lain yang tidak sejajar. Sudut dalam berseberangan ini memiliki karakteristik yaitu besar sudut yang dimiliki itu sama. Adapun beberapa sudut yang memiliki karakteristik dalam berseberangan yaitu sebagai berikut:
∠A4 = ∠B1
∠A3 = ∠B2
Sudut Luar Berseberangan
Sudut luar berseberangan merupakan salah satu sudut yang terbentuk karena dua garis sejajar dipotong oleh sebuah garis lain yang tidak sejajar. Terbentuknya sudut ini termasuk dalam materi hubungan antar garis. Sudut luar berseberangan ini memiliki karakteristik yaitu besar sudut yang dimiliki itu sama. Adapun beberapa sudut yang memiliki karakteristik luar berseberangan yaitu sebagai berikut:
∠A1 = ∠B4
∠A2= ∠B3
Sudut Bertolak Belakang
Sudut bertolak belakang merupakan salah satu sudut yang terbentuk karena dua garis sejajar dipotong oleh sebuah garis lain yang tidak sejajar. Terbentuknya sudut ini termasuk dalam materi hubungan antara dua garis. Sudut bertolak belakang ini memiliki karakteristik yaitu besar sudut yang dimiliki itu sama. Adapun beberapa sudut yang memiliki karakteristik bertolak belakang yaitu sebagai berikut:
∠A1 = ∠A4
∠A2= ∠A3
∠B1 = ∠B4
∠B2 = ∠B3
Sudut Dalam Sepihak
Sudut dalam sepihak merupakan salah satu sudut yang terbentuk karena dua garis sejajar dipotong oleh sebuah garis lain yang tidak sejajar. Terbentuknya sudut ini termasuk dalam materi hubungan dua garis. Sudut dalam sepihak ini memiliki karakteristik yaitu besar sudut total yang dimiliki berjumlah 180°. Adapun beberapa sudut yang memiliki karakteristik dalam sepihak yaitu sebagai berikut:
∠A3 + ∠B1 = 180°
∠A4 + ∠B2 = 180°
Sudut Luar Sepihak
Sudut luar sepihak merupakan salah satu sudut yang terbentuk karena dua garis sejajar dipotong oleh sebuah garis lain yang tidak sejajar. Sudut luar sepihak ini memiliki karakteristik yaitu besar sudut total yang dimiliki berjumlah 180°. Adapun beberapa sudut yang memiliki karakteristik luar sepihak yaitu sebagai berikut:
∠A1 + ∠B3 = 180°
∠A2 + ∠B4 = 180°
Contoh Soal Hubungan Antara Dua Garis
Setelah menjelaskan tentang materi hubungan antar garis di atas. Selanjutnya saya akan membagikan contoh soal hubungan dua garis beserta pembahasannya. Adapun contoh soal dan jawabannya yaitu sebagai berikut:
Perhatikan gambar di bawah ini!
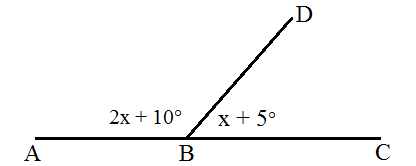
Tentukan besar pelurus sudut ABD?
Jawab.
Dua sudut saling berpelurus memiliki jumlah total sebesar 180º. Maka dari itu:
(2x + 10)º + (x + 5)º = 180º
3x + 15º = 180º
3x = 180º – 15º
3x = 165º
x = 55º
Besar pelurus sudut ABD = besar sudut CBD. Sehingga:
m∠CBD = x + 5º
m∠ABD = 55º + 5º
m∠ABD = 60º
Jadi besar pelurus sudut ABD ialah 60º.
Demikianlah penjelasan mengenai hubungan antar garis kelas 4 SD semester 2 dan contoh soalnya terlengkap. Hubungan antara dua garis tersebut dapat berupa berpotongan, bersilangan, sejajar dan berimpit.. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.