Materi Irisan Kerucut (Lingkaran, Elips, Parabola dan Hiperbola) – Dalam pelajaran Matematika terdapat pembahasan mengenai irisan kerucut. Materi matematika ini merupakan sebuah lokus dengan bentuk kurva dua dimensi dari semua titik. Terbentuknya kurva itu berasal dari sebuah kerucut yang beririsan dengan sebuah bidang. Apakah anda tahu apa saja macam macam irisan kerucut itu? Jenis jenis irisan kerucut pada dasarnya dapat dibagi menjadi beberapa bentuk seperti elips, hiperbola, lingkaran dan parabola. Setiap bentuk irisan kerucut ini memiliki rumusnya sendiri sendiri. Kerucut ialah bangun ruang yang memiliki bentuk alas berupa lingkaran. Kerucut memiliki sisi yang berjumlah dua yakni sisi lengkung yang dijadikan selimut kerucut dan sisi alas dengan bentuk lingkaran.
Apabila dari berbagai arah terjadi pengirisan kerucut, maka bentuk irisan yang dihasilkan dapat menjadi beberapa bangun. Bangun irisan kerucut ini menghasilkan bentuk elips, hiperbola, lingkaran maupun parabola. Untuk itulah bangun bangun ini dapat dijadikan menjadi jenis jenis irisan kerucut. Apakah anda tahu apa saja persamaan dalam materi irisan kerucut itu? Jika pemotongan kerucut dilakukan secara mendatar, maka potongan kerucut yang dihasilkan akan berbentuk lingkaran. Kemudian bentuknya akan menjadi parabola atau elips jika pemotongan kerucut mengarah pada sudut tertentu. Sedangkan bentuknya akan menjadi hiperbola apabila kerucut dipotong secara tegak.
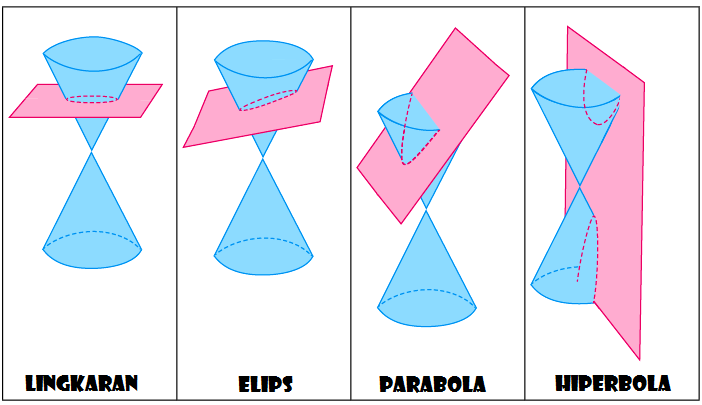
Pengertian irisan kerucut ialah lokus dengan bentuk kurva dua dimensi yang berasal dari semua titik dalam sebuah bidang hingga irisan kerucut ini dapat terbentuk. Irisan kerucut pertama kali ditemukan oleh Matematikawan Yunani bernama Apollonius dari Perga pada awal abad ke 2 SM yang dipelajari secara sistematik. Materi ini memang membentuk beberapa bangun lainnya. Setiap bangun irisan kerucut memiliki persamaan atau rumusnya sendiri sendiri. Pada kesempatan kali ini saya akan mendalami materi irisan kerucut, baik bentuk potongan lingkaran, elips, hiperbola maupun parabola.
Karena rumus hitung dari setiap bentuk memili tingkat kesulitan tingga, maka simaklah pembahasan secara seksama. Karena sedikit banyak materi tersebut akan muncul sebagai butir soal ujian ketika ujian berlangsung. Langsung saja, simaklah artikel di bawah sampai selesai.
Materi Irisan Kerucut (Lingkaran, Elips, Parabola dan Hiperbola)
Apa yang muncul di benak kalian ketika ditanya apa itu kerucut? pasti hampir semua menjawab bentuk menyerupai cone ice cream. Secara garis besar definisi tersebut memang benar. Tapi tak semua siswa tau jika sebuah irisan kerucut mampu menghasilkan bentuk yang berbeda.
Ketika berada di bangku Sekolah Menengah Atas tentunya telah diajarkan cara menghitung irisan kerucut. Dalam materi tersebut kita akan menjumpai rumus irisan kerucut di setiap bentuknya. Setiap jenis irisan kerucut akan menghasilkan bentuk berbeda dan menghasilkan bentuk baru. Kemudian materi Matematika ini juga sering keluar dalam soal soal ujian, baik ujian Nasional maupun ujian Sekolah.
Menurut saya pribadi, bukan perkara mudah untuk menghitung irisan kerucut. Karena mau atau tidak kita akan dipaksa menghafal rumus elips, parabola, hiperbola, dan lingkaran di saat bersamaan. Selain itu, siswa juga dituntut harus teliti dalam menghitung karena sedikit saja kesalahan saat memasukan angka hasilnya pun akan berbeda.
Baca juga : Contoh Soal Peluang Beserta Pembahasan Terlengkap
Seperti yang telah kita ketahui bahwa pengertian irisan kerucut adalah lokus dengan bentuk kurva dua dimensi yang berasal dari semua titik dalam sebuah bidang hingga irisan kerucut ini dapat terbentuk. Dari pengertian tersebut pastinya anda memiliki gambaran mengenai materi irisan kerucut. Di bawah ini terdapat pembahasan mengenai jenis jenis irisan kerucut. Berikut penjelasan selengkapnya:
Lingkaran
Bentuk irisan kerucut yang pertama ialah lingkaran. Lingkaran merupakan macam irisan kerucut yang terbentuk karena pemotongan suatu bidang dilakukan dengan arah mendatar. Dalam materi ini terdapat persamaan lingkaran dengan bentuk umum antara pusat dan jari jari yang berbeda. Persamaan lingkaran ini memiliki bentuk umum yang dapat dibagi menjadi dua jenis menurut pusatnya. Letak pusat lingkaran ada di sebuah titik koordinat kartesius P(a,b) ataupun di pusat koordinat kartesius O(0,0).
Persamaan lingkaran juga dapat berbentuk x² + y² + Ax + By + C = 0. Dalam materi irisan kerucut berbentuk lingkaran tersebut tentunya memiliki rumus yang berbeda beda setiap titiknya dalam koordinat kartesius. Di bawah ini terdapat rumus persamaan lingkaran yang berhasil di bentuk yaitu sebagai berikut:
Persamaan Lingkaran Jari Jari r dengan Pusat O (0,0)
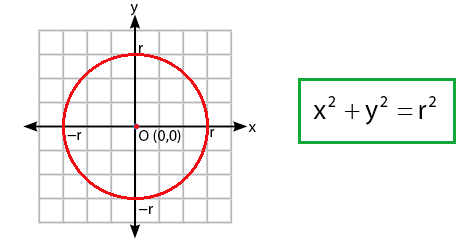
Persamaan lingkaran yang pertama memiliki jari jari r dengan pusat O(0,0). Jika dinyatakan dalam bentuk rumus dan gambar, maka akan menjadi seperti di bawah ini:
Persamaan Lingkaran Jari Jari r dengan Pusat P (a,b)
Persamaan lingkaran selanjutnya memiliki jari jari r dengan pusat P(a,b). Jika dinyatakan dalam bentuk rumus dan gambar, maka akan menjadi seperti di bawah ini:
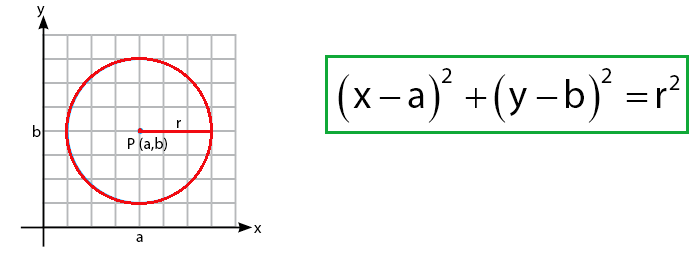
Bentuk Umum pada Persamaan Lingkaran
Selanjutnya saya akan membagikan materi irisan kerucut berbentuk persamaan lingkaran secara umum. Di bawah ini terdapat persamaan lingkaran secara umum yaitu meliputi:
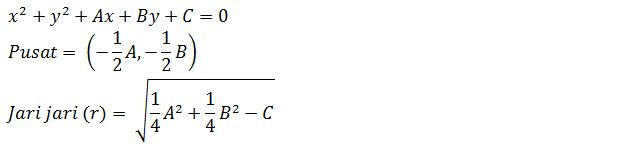
Elips
Kita akan melanjutkan pembahasan materi irisan kerucut pada bentuk elips. Elips memiliki bentuk yang menyerupai lingkaran yang dipipihkan. Elips tersebut memiliki beberapa bagian penting seperti sumbu minor, sumbu mayor, puncak elips, latus rectum, pusat elips, fokus elips dan sebagainya. Elips ini dapat dibagi menjadi dua jenis yaitu elips vertikal dan elips horizontal.
Tak banyak siswa yang mengetahui rumus elips karena materi tersebut memang hanya diajarkan secara singakat. Meski bisa menjumpai pembahasanya di buku pedoman tapi tak serta merta membuat kita paham cara menghitungnya. Maka dari itu, untuk menambah wawasan simaklah penjelasan di bawah.
Elips Horizontal
Elips horizontal memang termasuk dalam jenis irisan kerucut yang bentuknya seperti pipihan lingkaran. Jika diukur sumbunya, maka sumbu X akan lebih panjang daripada huruf Y. Inilah alasan mengapa jenis elips satu ini disebut horizontal karena bagian memanjangnya cenderung datar ke samping. Jika kalian masih bingung silahkan simak ilustrasi gambar di bawah:
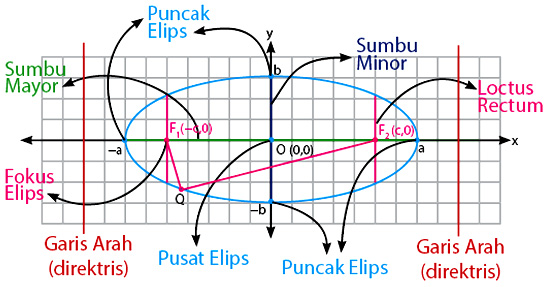
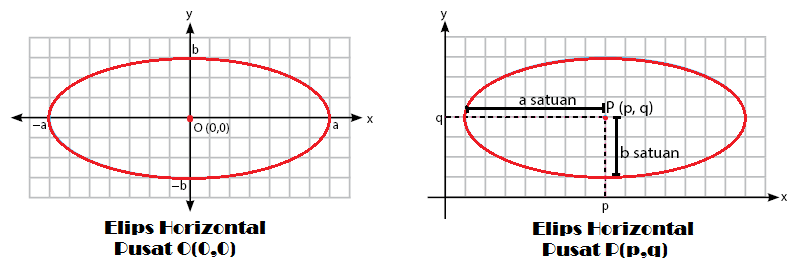
Elips horizontal pada dasarnya masih dapat dibagi menjadi dua jenis berdasarkan pusatnya. Jenis irisan kerucut ini dapat berupa elips horizontal dengan pusat O(0,0) dan dengan pusat P(p,q). Untuk lebih jelasnya perhatikan gambar di bawah ini:
Baca juga : Tabel Kebenaran Konjungsi, Disjungsi, Implikasi, dan Biimplikasi
Berdasarkan gambar elips horizontal di atas, kita dapat menemukan persamaan materi irisan kerucut di dalamnya. Adapun rumus persamaan pada elips horizontal yaitu sebagai berikut:
Berpusat di O(0,0)
- Fokus memiliki persamaan (±c,0).
- Sumbu Mayor memiliki panjang 2a.
- Sumbu Minor memiliki panjang 2b
- Puncak memiliki persamaan (±a,0) dan (0,±b)
- Memiliki persamaan secara umum berbentuk
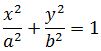 .
. - Memiliki direktris (garis arah) berupa
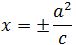 .
. - Loctus Rectumnya memiliki panjang
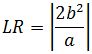 .
. - Eksentrisitasnya dapat berupa e = c / a.
Berpusat di P(p,q)
- Fokus memiliki persamaan (p ± c,q).
- Sumbu Mayor memiliki panjang 2a.
- Sumbu Minor memiliki panjang 2b
- Puncak memiliki persamaan (p ± a,q) dan (p,q ± b)
- Memiliki persamaan secara umum berbentuk
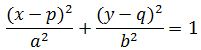 .
. - Memiliki direktris (garis arah) berupa
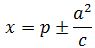 .
. - Loctus Rectumnya memiliki panjang
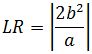 .
. - Eksentrisitasnya dapat berupa e = c / a.
Elips Vertikal
Elips verital juga termasuk dalam jenis irisan kerucut yang bentuknya sama seperti sebelumnya yakni lingkaran pipih seperti oval. Perbedaanya sumbu Y yang tegak lurus ke atas akan jauh lebih panjang daripada sumbu X yang notabenya mendatar. Nah, sebelum kita mempelajari rumus irisan kerucut satu ini alangkah baiknya simak ilustrasinya terlebih dulu:
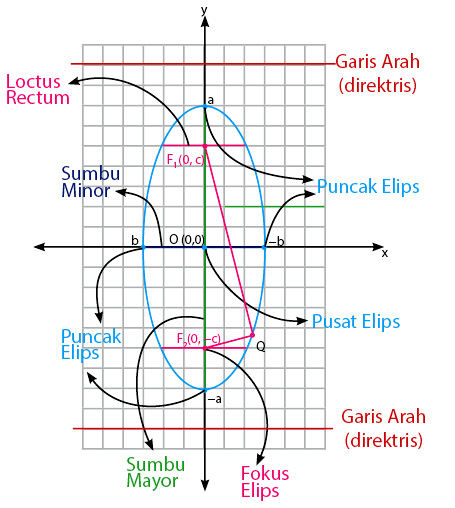
Berdasarkan pusatnya, kita masih bisa membagi elips vertikal menjadi dua macam. Jenis irisan kerucut ini dapat berupa elips vertikal dengan pusat O(0,0) dan pusat P(p,q). Terkadang, siswa kesulitan membedakannya karena letak dan rumus hitung yang hampir sama. Untuk lebih jelasnya perhatikan gambar di bawah ini:
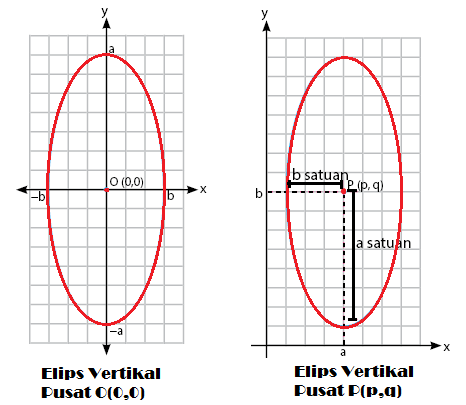
Berdasarkan gambar elips vertikal di atas, kita dapat menemukan persamaan persamaan materi irisan kerucut di dalamnya. Adapun persamaan persamaan pada elips vertikal yaitu sebagai berikut:
Berpusat di O(0,0)
- Fokus memiliki persamaan (±c,0).
- Sumbu Mayor memiliki panjang 2a.
- Sumbu Minor memiliki panjang 2b
- Puncak memiliki persamaan (±a,0) dan (0,±b)
- Memiliki persamaan secara umum berbentuk
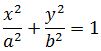 .
. - Memiliki direktris (garis arah) berupa
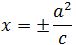 .
. - Loctus Rectumnya memiliki panjang
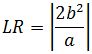 .
. - Eksentrisitasnya dapat berupa e = c / a.
Berpusat di P(p,q)
- Fokus memiliki persamaan (p ± c,q).
- Sumbu Mayor memiliki panjang 2a.
- Sumbu Minor memiliki panjang 2b
- Puncak memiliki persamaan (p ± a,q) dan (p,q ± b)
- Memiliki persamaan secara umum berbentuk
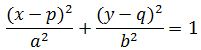 .
. - Memiliki direktris (garis arah) berupa
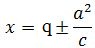 .
. - Loctus Rectumnya memiliki panjang
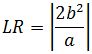 .
. - Eksentrisitasnya dapat berupa e = c / a.
Dalam elips terdapat fokus (hubungan a, b, dan c) yang berkaitan dengan puncak. Hubungan ini akan membentuk persamaan seperti di bawah ini:
- Persamaan elips horizontal berupa a² = b² + c², apabila a > b.
- Persamaan elips vertikal berupa b² = a² + c², apabila a < b.
Baca juga : Cara Menentukan Nilai Stasioner Beserta Contoh Soal
Parabola
Materi irisan kerucut selanjutnya ialah parabola. Parabola merupakan jenis irisan kerucut yang bentuknya seperti persamaan kuadrat dengan kurva mulusnya. Dalam materi ini terdapat jenis parabola yang bentuknya terbuka ke samping kiri atau kanan dan terbuka ke bawah atau ke atas. Parabola tersebut memiliki bentuk yang disesuaikan dengan rumus persamaannya. Jenis jenis parabola ini dapat berupa parabola vertikal dan parabola horizontal.
Bentuk parabola bisa kita jumpai dengan mudah dalam konteks kehidupan sehari-hari. Misalnya seperti bentuk parabola penangkap sinyal yang terkesan cekung ke dalam. Sayanngya beberapa siswa memiliki kesulitan ketika harus menyebutkan rumus parabola dan menghitungnya. Oleh karenanya, simakah pembahasan di bawah sampai selesai.
Parabola Dengan Puncak O (0,0)
Jenis parabola yang pertama memiliki puncak O(0,0). Jika dinyatakan dalam bentuk gambar, maka parabola vertikal dan parabola horizontalnya akan menjadi seperti di bawah ini:
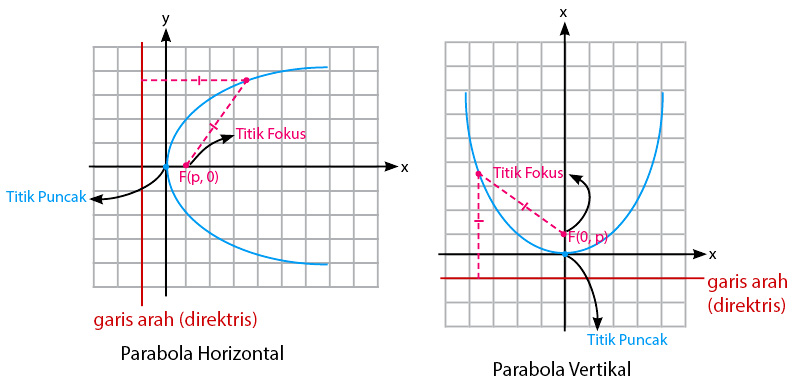
Materi irisan kerucut berbentuk parabola ini juga memiliki persamaannya secara umum, baik parabola vertikal maupun horizontal. Berikut persamaan parabola secara umum yaitu sebagai berikut:
Parabola Horizontal Puncak O(0,0)
- Memiliki fokus berupa (p,0).
- Memiliki direktris (garis arah) berupa x = -p.
- Persamaannya memiliki bentuk umum y² = 4px.
Parabola Vertikal Puncak O(0,0)
- Memiliki fokus berupa (0,p).
- Memiliki direktris (garis arah) berupa y = -p.
- Persamaannya memiliki bentuk umum x² = 4py.
Parabola Dengan Puncak P(a,b)
Jenis parabola selanjutnya memiliki puncak P(a,b). Jika dinyatakan dalam bentuk gambar, maka parabola vertikal dan parabola horizontalnya akan menjadi seperti di bawah ini:
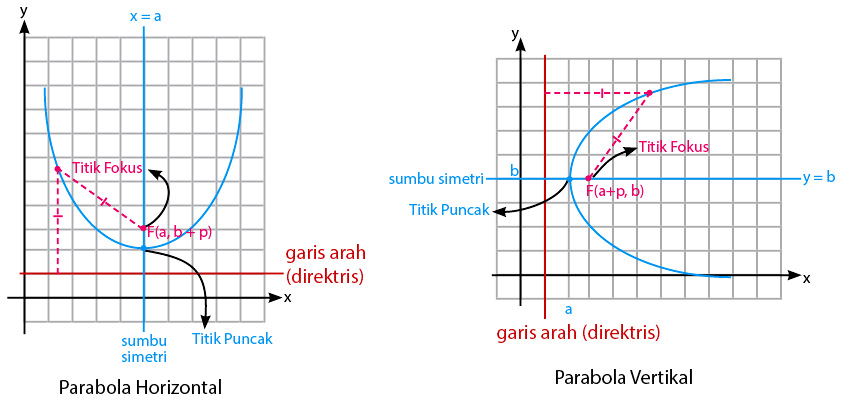
Materi irisan kerucut berbentuk parabola ini juga memiliki persamaannya secara umum, baik parabola vertikal maupun horizontal. Berikut persamaan parabola secara umum yaitu sebagai berikut:
Parabola Horizontal Puncak P(a,b)
- Memiliki fokus berupa (a + p,b).
- Memiliki direktris (garis arah) berupa x = a – p.
- Persamaannya memiliki bentuk umum (y – b)² = 4p(x – a).
Parabola Vertikal Puncak P(a,b)
- Memiliki fokus berupa (a,b + p).
- Memiliki direktris (garis arah) berupa y = b – p.
- Persamaannya memiliki bentuk umum (x – a)² = 4p(y – b).
Hiperbola
Hiperbola merupakan jenis irisan kerucut yang disusun oleh beberapa komponen seperti asimtot, titik fokus, kurva, titik puncak, direktris (garis arah) dan sebagainya. Dalam hiperbola ini memang terdapat berbagai komponen penyusun yang saling berhubungan sehingga terbentuk persamaan rumus umumnya.
Tak semua siswa familiar ketika ditanya seperti rumus hiperbola atau bagaimana cara mengerjakan contoh soalnya. Bahkan, materi irisan kerucut satu ini hanya disampaikan pada siswa SMA saja sedangkan jenjang seperti SMK dan madrasah jarang mendapatkannya. Padahal, ada dua jenis hiperbola yang harus kalian hafal ketika ujian. Yakni hiperbola horizontal maupun hiperbola vertikal, baik pusatnya di O(0,0) ataupun P(p,q).
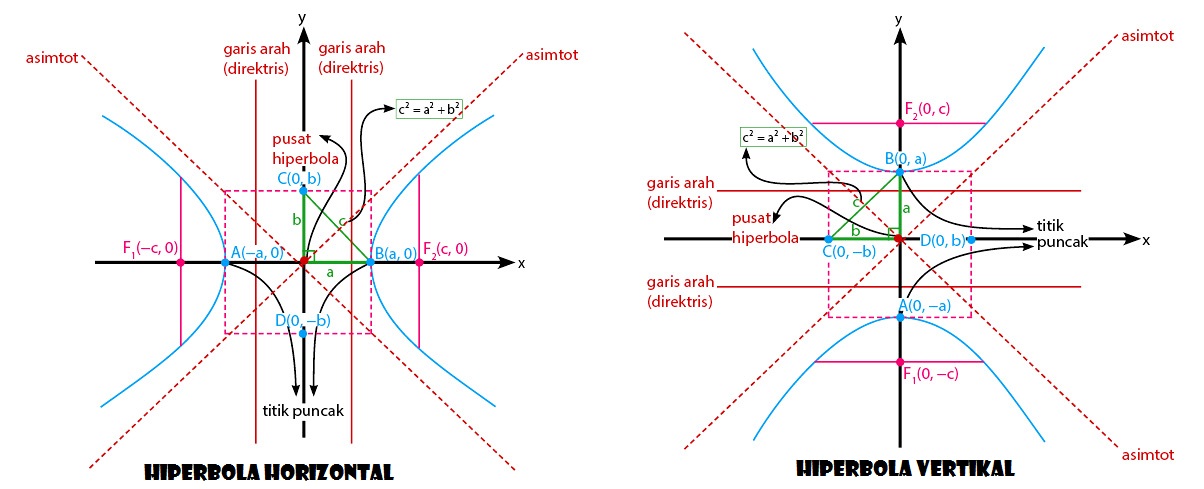
Hiperbola Dengan Pusat O (0,0)
Jenis hiperbola yang pertama memiliki pusat O(0,0). Jika dinyatakan dalam bentuk gambar, maka hiperbola vertikal dan hiperbola horizontalnya akan menjadi seperti di bawah ini:
Materi irisan kerucut berbentuk hiperbola ini juga memiliki persamaannya secara umum, baik hiperbola vertikal maupun hiperbola horizontal. Berikut persamaan hiperbola secara umum yaitu sebagai berikut:
Hiperbola Horizontal Pusat O(0,0)
- Memiliki fokus berupa (±c,0).
- Memiliki puncak berupa (±a,0)
- Memiliki direktris (garis arah) berupa x = ± a²/c.
- Memiliki asimtot berupa y = ± b/a.
- Memiliki eksentrisitas e = c/a.
- Loctus Rectumnya memiliki panjang LR =|2b²/a|
- Persamaannya memiliki bentuk umum x²/a² – y²/b² = 1.
Hiperbola Vertikal Pusat O(0,0)
- Memiliki fokus berupa (0,±c).
- Memiliki puncak berupa (0,±a)
- Memiliki direktris (garis arah) berupa x = ± a²/c.
- Memiliki asimtot berupa y = ± b/a.
- Memiliki eksentrisitas e = c/a.
- Loctus Rectumnya memiliki panjang LR =|2b²/a|
- Persamaannya memiliki bentuk umum x²/b² – y²/a² = 1.
Hiperbola Dengan Pusat P (p,q)
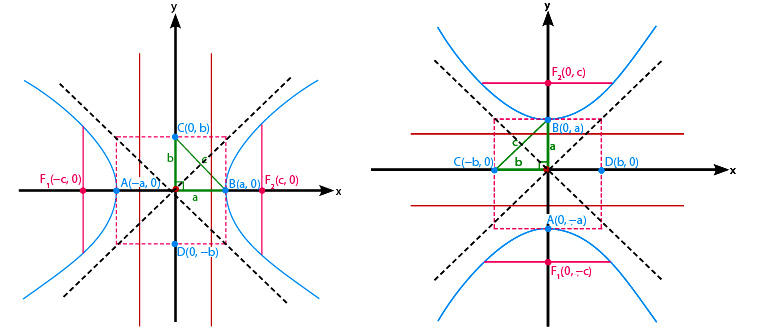
Materi irisan kerucut jenis hiperbola selanjutnya memiliki pusat P(p,q). Jika dinyatakan dalam bentuk gambar, maka hiperbola vertikal dan hiperbola horizontalnya akan menjadi seperti di bawah ini:
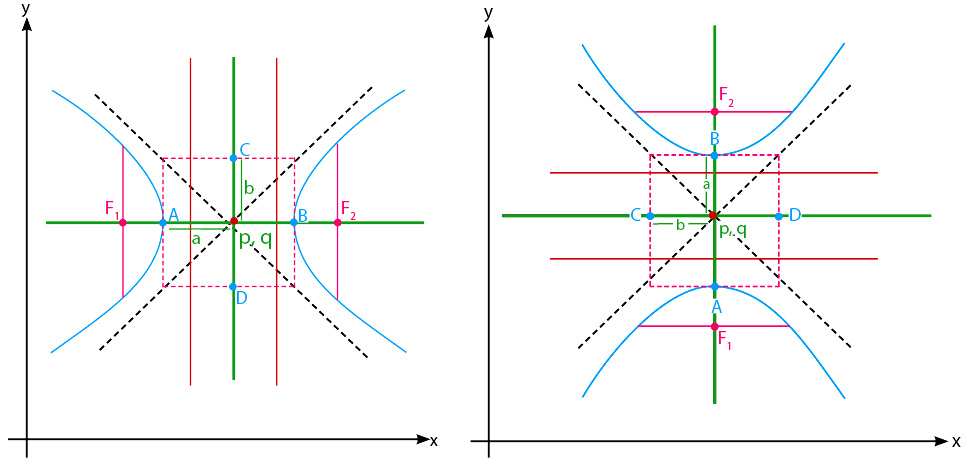
Materi irisan kerucut berbentuk hiperbola ini juga memiliki persamaannya secara umum, baik hiperbola vertikal maupun hiperbola horizontal. Berikut persamaan hiperbola secara umum yaitu sebagai berikut:
Hiperbola Horizontal Pusat P(p,q)
- Memiliki fokus berupa (p ± c,q).
- Memiliki puncak berupa (p ± a,q)
- Memiliki direktris (garis arah) berupa y = p ± a²/c.
- Memiliki asimtot berupa y – q = ± b/a(x – p).
- Loctus Rectumnya memiliki panjang LR =|2b²/a|
- Persamaannya memiliki bentuk umum (x – p)²/a² – (y – q)²/b² = 1.
Hiperbola Vertikal Pusat P(p,q)
- Memiliki fokus berupa (p,q ± c).
- Memiliki puncak berupa (p,q ± a)
- Memiliki direktris (garis arah) berupa y = q ± a²/c.
- Memiliki asimtot berupa y – q = ± b/a(x – p).
- Loctus Rectumnya memiliki panjang LR =|2b²/a|
- Persamaannya memiliki bentuk umum (x – p)²/b² – (y – q)²/a² = 1.
Demikianlah penjelasan mengenai materi irisan kerucut, baik bentuk potongan lingkaran, elips, hiperbola maupun parabola. Irisan kerucut dapat diartikan sebagai lokus dengan bentuk kurva dua dimensi yang berasal dari semua titik dalam sebuah bidang hingga irisan kerucut ini dapat terbentuk. Semoga artikel ini dapat bermanfaat dan terima kasih telah berkunjung di blog ini.


